【非比较排序】计算排序算法

news2025/2/25 15:50:20

CountSort计数排序

整体思想

图解分析

代码实现

时间复杂度&优缺分析

CountSort计数排序

计数排序是一种非比较排序，不需要像前面的排序一样去比较。

计数排序的特性总结：
1. 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
2. 时间复杂度：O(MAX(N,范围))
3. 空间复杂度：O(范围)

4. 稳定性：稳定

整体思想

思想：计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中

Count数组

Count数组中的元素需要全部初始化为0（calloc就可以满足这个要求）
Count元素是计算a数组元素个数出现的次数
Count数组的下标是a数组元素的范围
绝对隐射：范围0~max（a中最大的元素）
相对隐射：范围0~max-min <<<<<<<<< min~max
range = max-min+1（映射0~max-min，个数max-min+1)

整个流程

遍历一遍：找到最大值 / 最小值
计算出Count数组下标范围并且开辟动态空间
rangge=max-min+1
计数Count[a[i]-min]++ (i++)
相对隐射回去

注意tips

i和j能不能公用❓
a数组的元素可以是负数吗？
除了整型其他类型可以吗？
后置--&前置--

calloc>>>>>>calloc - C++ Reference (cplusplus.com)
Count的下标表示a的元素的范围
Count的元素表示a的元素出现的个数（计数）

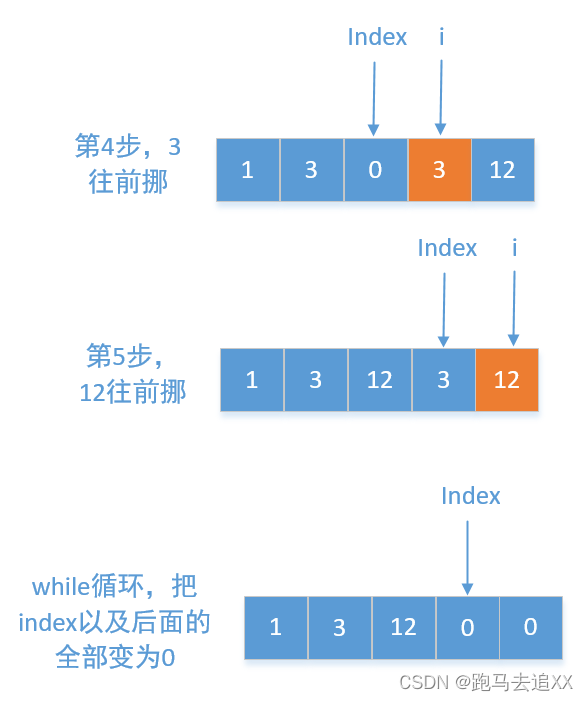
图解分析

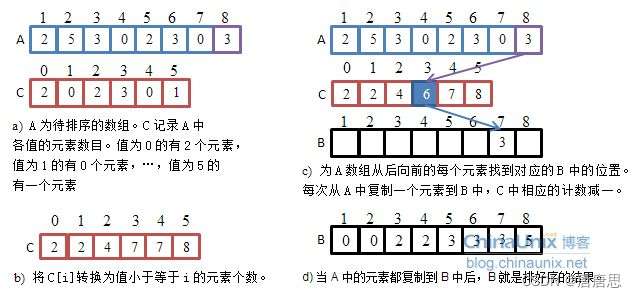
代码实现

void CountSort(int* a, int n)
{
	//找最大值/最小值/创建的tmp的范围在这个之间
	int max = a[0];
	int min = a[0];
	for (int i = 0; i < n; i++)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}

	int range = max - min + 1;//注意
	int* count = (int*)calloc(range, sizeof(int));
	//计数
	for (int j = 0; j < n; j++)
	{
		count[a[j]-min]++;
	}

	//相对隐射回去
	int i = 0;
	for (int k = 0; k < range; k++)
	{
		while (count[k]--)
		{
			a[i++] = k + min;
		}
	}
}