HuggingFists低代码平台提供Mysql,Postgresql,Oracle,ClickHouse等多种数据库连接插件及配套读写算子。提供ftp,sftp,百度盘,阿里云文件系统,腾讯文件系统等多种文件系统连接插件及配套读写算子。满足用户静态脱敏场景下各种数据源要求。

静态脱敏-数据库连接器

静态脱敏-文件系统连接器
配合算子平台提供的各种算法以及简单快捷的算子开发方式,可快速构建静态脱敏流程。
静态脱敏一般从已存在的数据库或数据集中获取数据,经过脱敏处理后写入新的数据库或文件,构建个简单的流程如下。
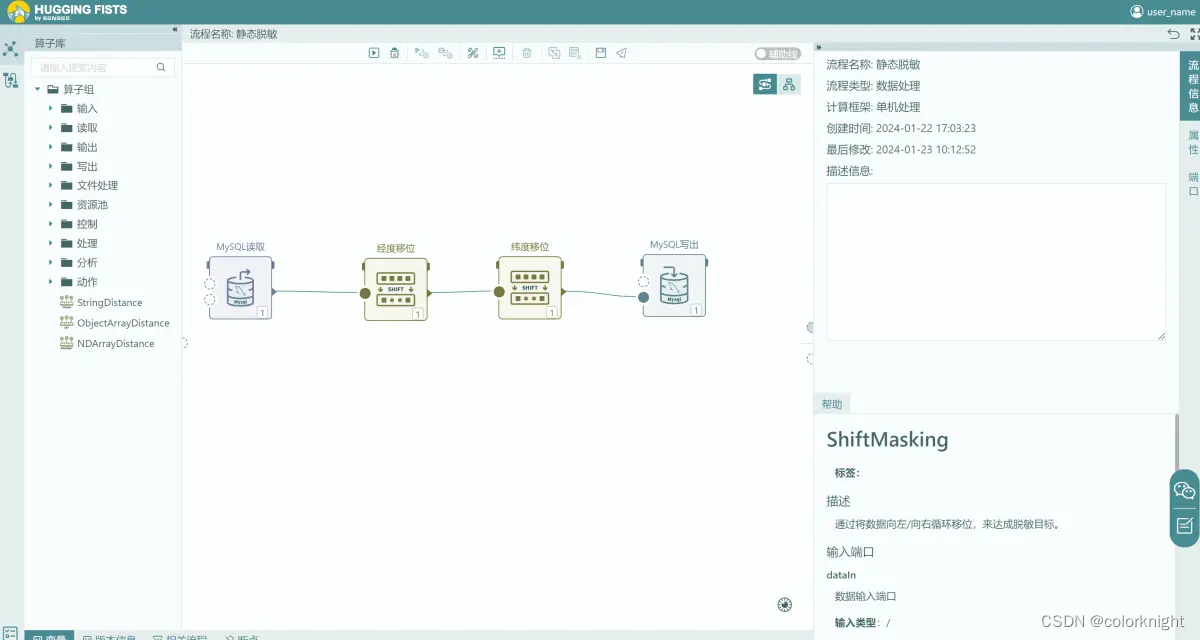
静态脱敏-简单脱敏
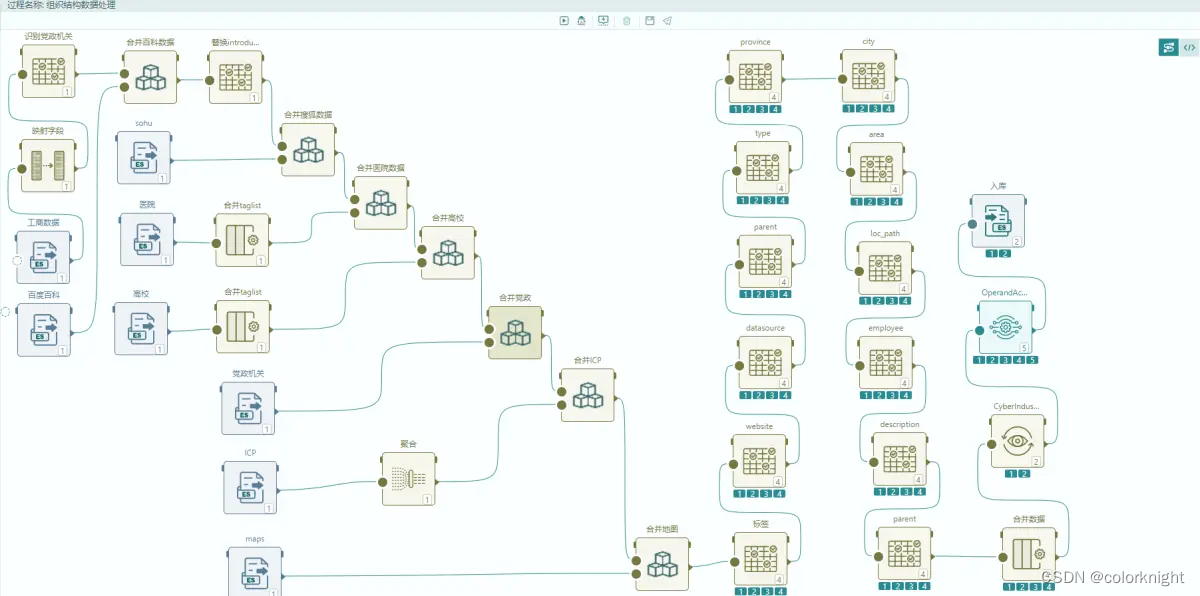
为了展示可以构建的流程复杂度,贴一个以前构建的数据处理流程。
数据流程以爬取的工商数据为基础,合并从百度百科,搜狐,医院,学校,党政机关,ICP,地图信息等,中间经过数据合并,去重,调用API接口识别行业,指定ID(MD5算法)等,最终入库。
工商数据70余w,其余数据几万到30w不等,最终20分钟处理完毕(单机模式)。