题目:78_子集(没看题解)
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例: 输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
#
算法思想:
子集问题,树上的结点都是目标集合,不需要剪枝。但要注意仍然是组合问题,集合是无序的,每次从 indexstart 开始。

代码:
import java.util.ArrayList;
import java.util.List;
class Solution {
List<Integer> list = new ArrayList<>();
List<List<Integer>> ans = new ArrayList<>();
void backtracking(List nums, int startindex) {
if (startindex >= nums.size()) { //无需剪枝
return;
}
for (int i = startindex; i < nums.size(); i++) {
list.add((Integer) nums.get(i));
ans.add(new ArrayList<>(list));
backtracking(nums, i + 1);
list.remove(list.size() - 1);
}
}
public List<List<Integer>> subsets(int[] nums) {
ArrayList<Integer> list = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
list.add(nums[i]);
}
backtracking(list, 0);
ans.add(new ArrayList<>());
return ans;
}
}题目:90_子集2
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
- 输入: [1,2,2]
- 输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]
#
算法思想:
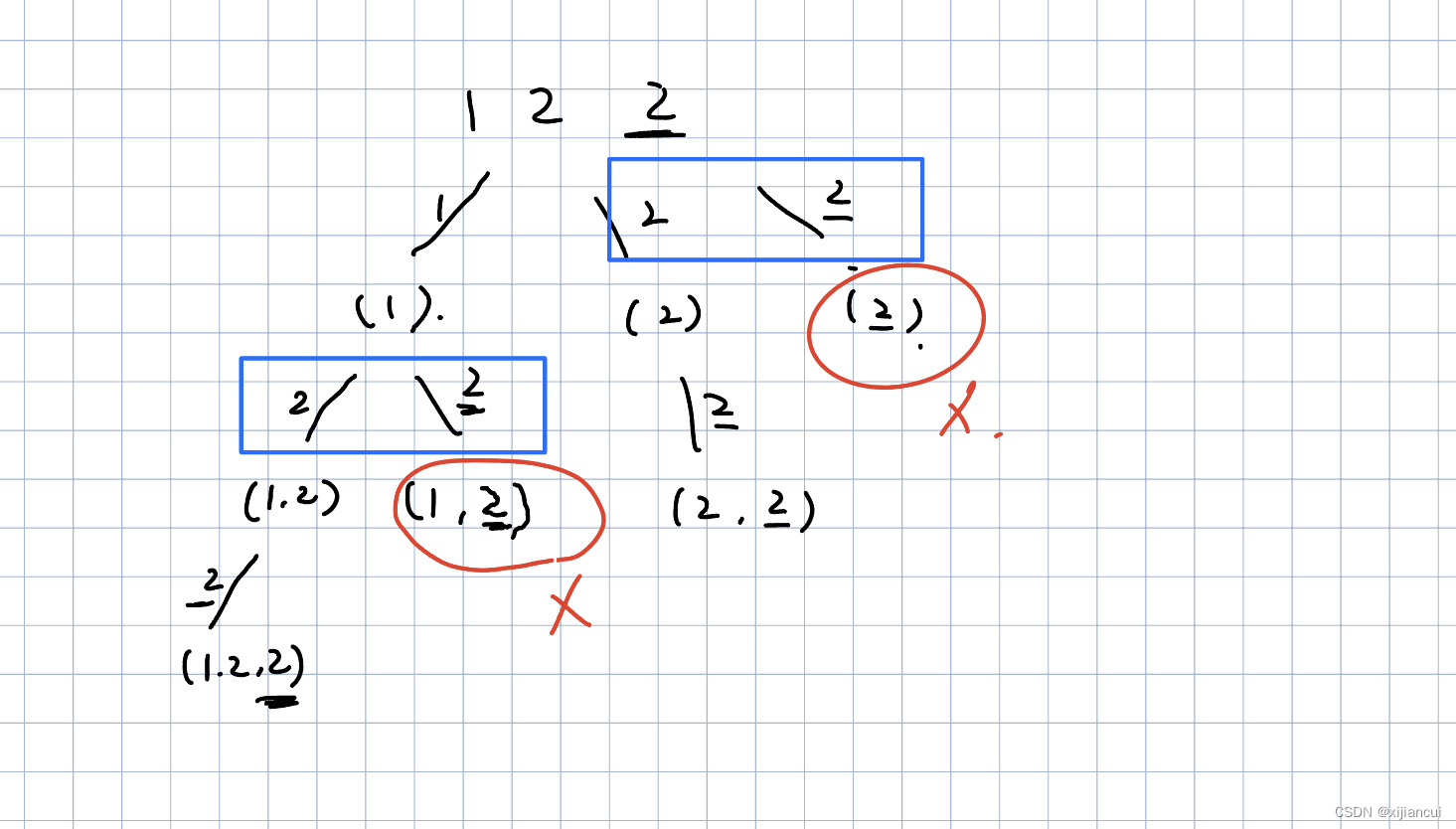
数组中包含重复元素,层间要去重。
去重思想,把数组变为递增有序数组,那么重复元素都在相邻位置。设置used数组,在枝上当前元素前一个重复元素 used 为true,在同一层当前元素的前一个相同元素由于回溯 used 为false。
则当满足 i > 0 && list.get(i - 1) == list.get(i) && used[i - 1] == false;
跳过,防止重复
代码:
import java.lang.reflect.Array;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
//解法1:先把所有集合回溯法求出来,最后再去重。
//但是有部分用例通过不了
//class Solution {
// List<Integer> list = new ArrayList<>();
// List<List<Integer>> ans = new ArrayList<>();
//
// boolean isContain(List<Integer> list, List<List<Integer>> ans){
// for (int i = 0; i < ans.size(); i++) {
// //先对两个集合中元素进行排序,这样就能保证元素值相同equals比较结果就为true
//
// if(ans.get(i).equals(list))
// return false;
// }
// return true;
// }
//
// void backtracking(List nums, int startindex) {
// if (startindex >= nums.size()) {
// return;
// }
// for (int i = startindex; i < nums.size(); i++) {
// list.add((Integer) nums.get(i));
// if(isContain(list,ans)) {
// ans.add(new ArrayList<>(list));
// }
// backtracking(nums, i + 1);
// list.remove(list.size() - 1);
// }
//
// }
//
// public List<List<Integer>> subsetsWithDup(int[] nums) {
// ArrayList<Integer> list = new ArrayList<>();
// for (int i = 0; i < nums.length; i++) {
// list.add(nums[i]);
// }
// backtracking(list, 0);
// ans.add(new ArrayList<>());
// return ans;
//
// }
//}
//回溯的过程中减枝
class Solution {
List<Integer> path = new ArrayList<>();
List<List<Integer>> ans = new ArrayList<>();
boolean[] used = new boolean[11];
void backtracking(List list, int startindex) {
if (startindex >= list.size()) {
return;
}
for (int i = startindex; i < list.size(); i++) { // 组合问题无序,每次从startindex开始
if (i > 0 && list.get(i - 1) == list.get(i) && used[i - 1] == false) { // 去除同层重复元素
continue;
}
path.add((Integer) list.get(i));
used[i] = true;
ans.add(new ArrayList<>(path));
// 递归
backtracking(list, i + 1);
// 回溯
path.remove(path.size() - 1);
used[i] = false;
}
}
public List<List<Integer>> subsetsWithDup(int[] nums) {
Arrays.sort(nums); // 给数组排序
List<Integer> list = new ArrayList<>();
// 手动把 nums[] 转 ArrayList
for (int i = 0; i < nums.length; i++) {
list.add(nums[i]);
}
backtracking(list, 0);
ans.add(new ArrayList<>()); // 加入空集合
return ans;
}
}