文章目录
- 面试经典150题【31-40】
- 76.最小覆盖字串
- 36.有效的数独
- 54.螺旋矩阵
- 48.旋转图像
- 73.矩阵置零
- 289.生命游戏
- 383.赎金信
- 205.同构字符串
- 290.单词规律
- 242.有效的字母异位词
面试经典150题【31-40】
76.最小覆盖字串

基本思路很简单,就是先移动右边到合适位置。再移动左边到破戒,再移动位置到合适位置。
判断合适位置是 count0, 此时need[] 里面也都是0 或 <0 的元素。
public class LC76 {
public String minWindow(String s, String t) {
if(s == null || s.isEmpty() ||t==null || t.isEmpty()){
return "";
}
int []need=new int[128];
for(int i=0;i<t.length();i++){
need[t.charAt(i)]++;
}
//l是当前左边界,r是当前右边界,size记录窗口大小,count是需求的字符个数,start是最小覆盖串开始的index
int l = 0, r = 0, size = Integer.MAX_VALUE, count = t.length(), start = 0;
//如果need[]<0,说明无关紧要。如果need[]==0,则说明是被需要关注的元素
while(r<s.length()){
//对右边进行处理
char c=s.charAt(r);
if(need[c]>0){ //是值得关注的元素
count--;
}
need[c]--;
if(count==0){ //已经塞满了关注的元素了
//移动左指针
while(l<r && need[s.charAt(l)]<0){
need[s.charAt(l)]++;
l++;
}
//此时need==0,说明又满足了,开始统计
if(r-l+1<size){
size = r-l+1;
start = l;
}
//又要向右移动,但是肯定和最小值无关了,开始破戒
need[s.charAt(l)]++;
l++;
count++;
}
r++;
}
return size == Integer.MAX_VALUE ? "" : s.substring(start, start + size);
}
}
36.有效的数独
一定是9×9的,
在第 i 个行中是否出现过
在第 j 个列中是否出现过
在第 j/3 + (i/3)*3个box中是否出现过.
定义三个数组,int [][]row, row[i][j], i代表第几行,j代表出现的元素。
box[i][j], i代表第几个小格子,j代表出现的元素。

class Solution {
public boolean isValidSudoku(char[][] board) {
int[][] row = new int[9][10];
int[][] col = new int[9][10];
int[][] box = new int[9][10];
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] == '.') {
continue;
}
int curNum = board[i][j] - '0';
if (row[i][curNum] == 1) {
return false;
}
if (col[j][curNum] == 1) {
return false;
}
if (box[j / 3 + (i / 3) * 3][curNum] == 1) {
return false;
}
row[i][curNum] = 1;
col[j][curNum] = 1;
box[j / 3 + (i / 3) * 3][curNum] = 1;
}
}
return true;
}
}
54.螺旋矩阵
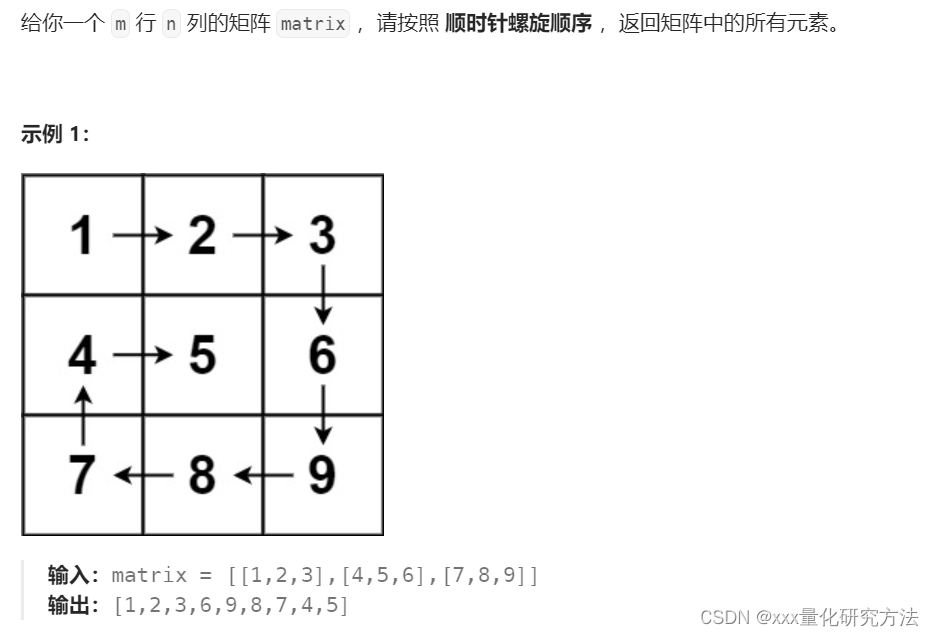
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int up = 0;
int down = m - 1;
int left = 0;
int right = n - 1;
List<Integer> ans = new ArrayList<>();
while (true) {
for (int i = left; i <= right; i++)
ans.add(matrix[up][i]);
if (++up > down)
break;
for (int i = up; i <= down; i++)
ans.add(matrix[i][right]);
if (--right < left)
break;
for (int i = right; i >= left; i--)
ans.add(matrix[down][i]);
if (--down < up)
break;
for (int i = down; i >= up; i--)
ans.add(matrix[i][left]);
if (++left > right)
break;
}
return ans;
}
}
48.旋转图像
关键是找到公式: matrix[i][j] -> matrix[j][n-1-i]
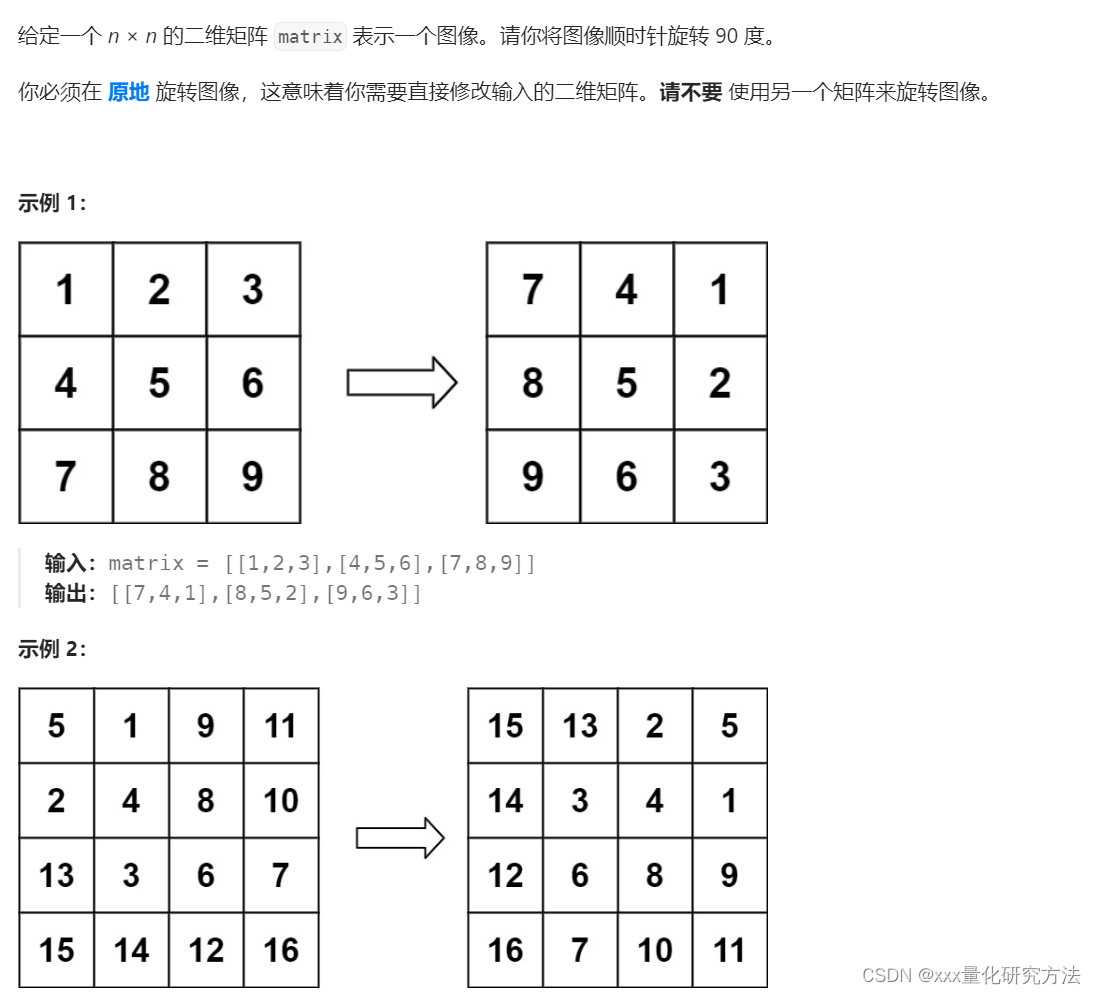
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < (n + 1) / 2; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[n - 1 - j][i];
matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
matrix[j][n - 1 - i] = tmp;
}
}
}
}
73.矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
还是用两个辅助数组,一个判断某一行,一个判断某一列。舒服。
289.生命游戏
暴力模拟就行。dxdy代表你移动的旁边的8个位置。
int[] dx = { -1, 1, 0, 0, -1, -1, 1, 1 };
int[] dy = { 0, 0, -1, 1, -1, 1, -1, 1 };
for (int k = 0; k < 8; k++) {
int nx = x + dx[k];
int ny = y + dy[k];
if (nx < 0 || nx >= m || ny < 0 || ny >= n)
continue;
// 如果这个位置为 0,代表当前轮是死的,不需要算进去
// 如果这个位置为 1,代表当前轮是活得,需要算进去
// 如果这个位置为 2,代表当前轮是死的(状态10,下一轮是活的),不需要算进去
// 如果这个位置为 3,代表是当前轮是活的(状态11,下一轮也是活的),需要算进去
cnt += (board[nx][ny] & 1);
}
383.赎金信
int[] a = new int[26]; 用这个做个小哈希表就行
205.同构字符串
每个出现的字符都应当映射到另一个字符,同时不改变字符的顺序。不同字符不能映射到同一个字符上。
要满足最后一条,应该建立两个hash表, m ->t ; t->m
如果只建立一个hash表, abb -> rrr 会成立,但是其应该不成立。
290.单词规律
也是典型的双射问题,两个哈希表就解决了。
如果两个字符串完全不一样,也可以只用一个哈希表。利用hashmap的put操作的返回值的特性。
如果key不存在,插入成功,返回null;如果key存在,返回之前对应的value。
先将字符串截断 String[] words = str.split(" ");
然后用map.put(words[i],i) 与 map.put(s[i],i)判等就行
242.有效的字母异位词
也是hashmp,第一个字符串遍历去++,第二个字符串遍历去–。
最后判断是否所有元素均为0即可。