本专栏内容为：算法学习专栏，分为优选算法专栏，贪心算法专栏，动态规划专栏以及递归，搜索与回溯算法专栏四部分。 通过本专栏的深入学习，你可以了解并掌握算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：动态规划专栏
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

题目来源

本题来源为：

Leetcode377. 组合总和 Ⅳ

题目描述

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

算法原理

1.状态表示

根据问题分析，分析出重复子问题

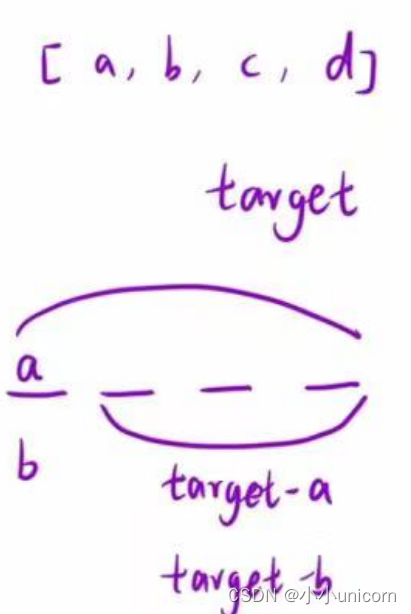
经验+题目要求

对于本题而言就是：

dp[i]表示：凑成总和为i，一共有多少种排列数

2.状态转移方程

因此状态方程为：

dp[i]+=dp[i-x];

3.初始化

dp[0]=1

4.填表顺序

从左往右

5.返回值

返回dp[target]

代码实现

动态规划的代码基本就是固定的四步：

1.创建dp表
2.初始化
3.填表
4.返回值

本题完整代码实现：

class Solution 
{
public:
    int combinationSum4(vector<int>& nums, int target) 
    {
        vector<double> dp(target+1);
        dp[0]=1;
        for(int i=1;i<=target;i++)
        {
            for(auto x:nums)
                if(i>=x)
                    dp[i]+=dp[i-x];
        }
        return dp[target];
    }
};