day40打卡

343. 整数拆分

状态表示

​ dp[i] 表示将正整数i拆分成至少两个正整数的和之后，这些正整数的最大乘积

状态转移方程

​ i >= 2 时，对正整数i拆出的第一个正整数是j，则有：

• 将i拆分为 j 和 i-j，且 i-j不再拆分为多个正整数，此时的积为i * (i-j)
• 将i拆分为 j 和 i-j的和，且 i-j再拆分为多个正整数，此时的积为i * dp[i-j]

初始化

​ 0 不是正整数，1是最小的正整数，0和1都不能拆分，因此 dp[0] = dp[1] = 0，dp[2] = 1

填表顺序

​ 从左到右

返回值

​ dp[n]

class Solution {
public:
    int integerBreak(int n) {
        //创建dp数组
        vector<int> dp(n+1);
        //初始化
        dp[2] = 1;
        //填表
        for(int i = 3; i <= n; i++)
        {
            for(int j = 1; j < i; j++)
            {
                dp[i] = max(dp[i], max(j * (i - j), j * dp[i-j]));
            }
        }
        //返回值
        return dp[n];
    }
};

96. 不同的二叉搜索树

状态表示

​ 1到i为节点组成的二叉搜索树的个数为dp[i]

状态转移方程

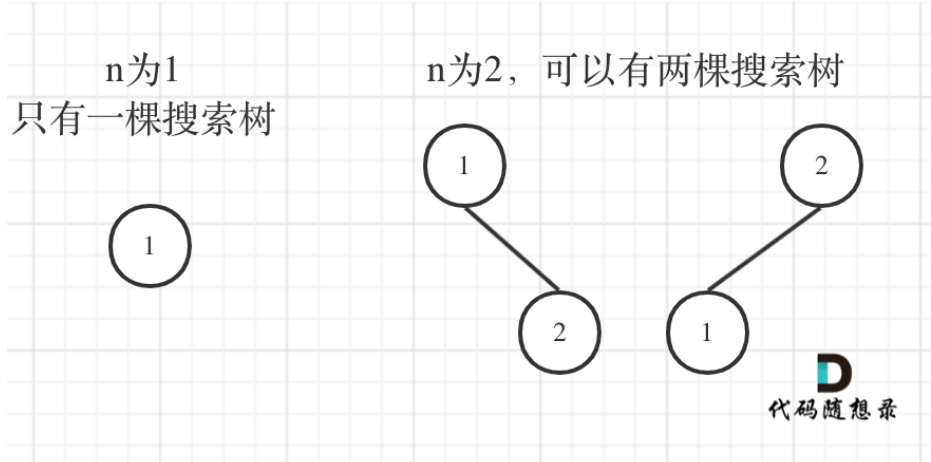
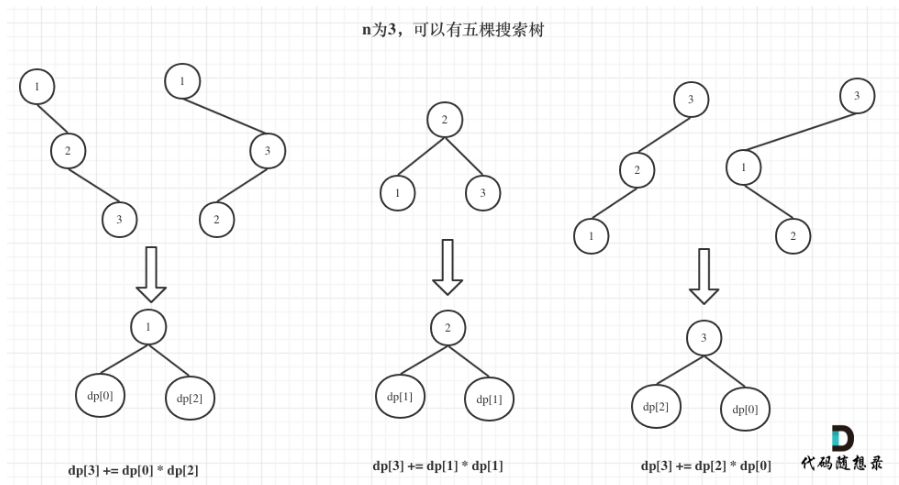
​ dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]

初始化

​ dp[0] = 1

填表顺序

​ 从左到右

返回值

​ dp[n]

class Solution {
public:
    int numTrees(int n) {
        //创建dp数组
        vector<int> dp(n+1);
        //初始化
        dp[0] = 1;
        //填表
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= i; j++)
            {
                dp[i] += dp[j-1] * dp[i-j];
            }
        }
        //返回值
        return dp[n];
    }
};