目录
原题描述:
题目描述
输入格式
输出格式
样例输入
样例输出
样例解释
数据规模
主要思路:
小细节:
代码code:
原题描述:
时间限制: 1000ms
空间限制: 524288kB
题目描述
很久很久以前,一座大陆桥横跨西伯利亚东端与美洲大陆西端。
处于进化早期的人类,正以部落的形式在大陆上游荡、捕猎,四海为家。在饥饿与寒冷折磨下,人们不断迁徙。在不知不觉中,也许有一支队伍、也许有许多支队伍,跨过了大陆桥,来到了美洲大陆。人类繁衍与进化的脚步自此迈上了美洲大陆。
然而,板块位移,地质变迁,陆地慢慢被大海淹没,广阔的海峡将亚欧大陆和美洲大陆的人类分隔开来。也许是万年,也许是十万年,两岸的人类才能再度相见。
大陆架可以看作一个 的矩形区域,区域内有一些格子已经被海洋所淹没。在接下来的
年里,区域内还有一些格子会逐个沉没。那么到底是哪一年两座大陆才会分隔开来呢?
输入格式
第一行一个整数 T 代表数据组数。
每组数据第一行两个整数 n 和 m,
接下来 n 行每行 m 个整数,为 1 表示已经被淹没,为 0 表示仍为陆地。
接下来一行一个整数 q,
接下来 q 行每行两个整数,表示沉没的格子坐标。
输出格式
每组数据输出一行,代表答案。如果 q 年之后还连通,输出-1
样例输入
1
4 6
011010
000010
100001
001000
7
0 3
1 5
1 3
0 0
1 2
2 4
2 1样例输出
4
样例解释
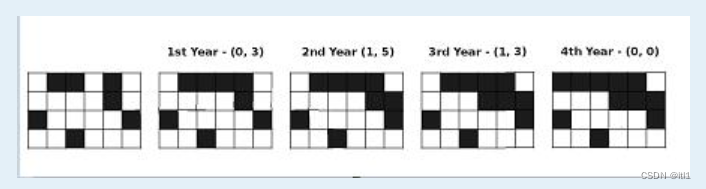
到第 4 年,无法从上面到达下面。
第3年可以从上面走到下面,我们可以想象输入是一个连接着上方和下方的桥。
第0年,我们可以这么走:
数据规模
主要思路:
这题你第一眼的感觉是否是对于每一年写个bfs判断能不能走到底,那我很荣幸的告诉你,恭喜你:TLE 0分。
有眼睛的人会先看一下数据范围(q<=n*m),接着看一下文章标签(二分),最后顺手来个三连
回归正题。
我们想,如果第mid年,不能从第一行走到第n行,那么mid+1~q年岂不是都不能从第一行到第n行(因为海水只会淹没更多的地方)
发现了啥???
没错单调性!!!
有单调性,你脑海里第一个会想到啥???
二分答案。
所以这题一切都简单了
但还有一个问题,二分找到的是可以从1走到n的情况(我是这样写的),所以ans不能直接=mid(因为mid不是答案)ans要=mid+1
小细节:
注意q的大小(n*m)所以数组要开500*500=250000
然后每次判断bfs的时候要vis清空,a数组的变化。
代码code:
#include<bits/stdc++.h>
using namespace std;
int t;
char a[1010][1010];
int vis[1010][1010];
int dx[]={0,1,0,-1};
int dy[]={1,0,-1,0};
int asd[1000010],fgh[1000010];
int n,m;
struct node
{
int x,y;
};
int q;
bool bfs(int mid)
{
memset(vis,0,sizeof(vis));
queue<node> q1;
for(int i=1;i<=min(mid,q);i++)//哪里被淹没了
{
vis[asd[i]][fgh[i]] = 1;
}
for(int i=0;i<m;i++)//哪里可以当起点
{
if(a[0][i] == '0'&&vis[0][i]!=1)
{
q1.push({0,i});
vis[0][i] = 1;
}
}
while(!q1.empty())//bfs
{
auto tmp = q1.front();
q1.pop();
if(tmp.x == n-1)
{
return 1;
}
for(int i=0;i<4;i++)
{
int tx=tmp.x+dx[i],ty=tmp.y+dy[i];
if(tx<0||tx>=n||ty<0||ty>=m||vis[tx][ty]||a[tx][ty] == '1')
{
continue;
}
vis[tx][ty] = 1;
q1.push({tx,ty});
}
}
return 0;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin>>t;
while(t--)
{
cin>>n>>m;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cin>>a[i][j];
}
}
cin>>q;
int flag=1;
for(int i=1;i<=q;i++)
{
cin>>asd[i]>>fgh[i];
}
int l=0,r=q+1;
int ans=INT_MAX;//二分
while(l<=r)
{
int mid=(l+r)/2;
if(bfs(mid))
{
l = mid+1;
ans = mid+1;
}
else
{
r = mid-1;
}
}
// cout<<bfs(4);
if(ans == INT_MAX)
{
cout<<-1<<'\n';
}
else
{
cout<<ans<<'\n';
}
}
return 0;
}