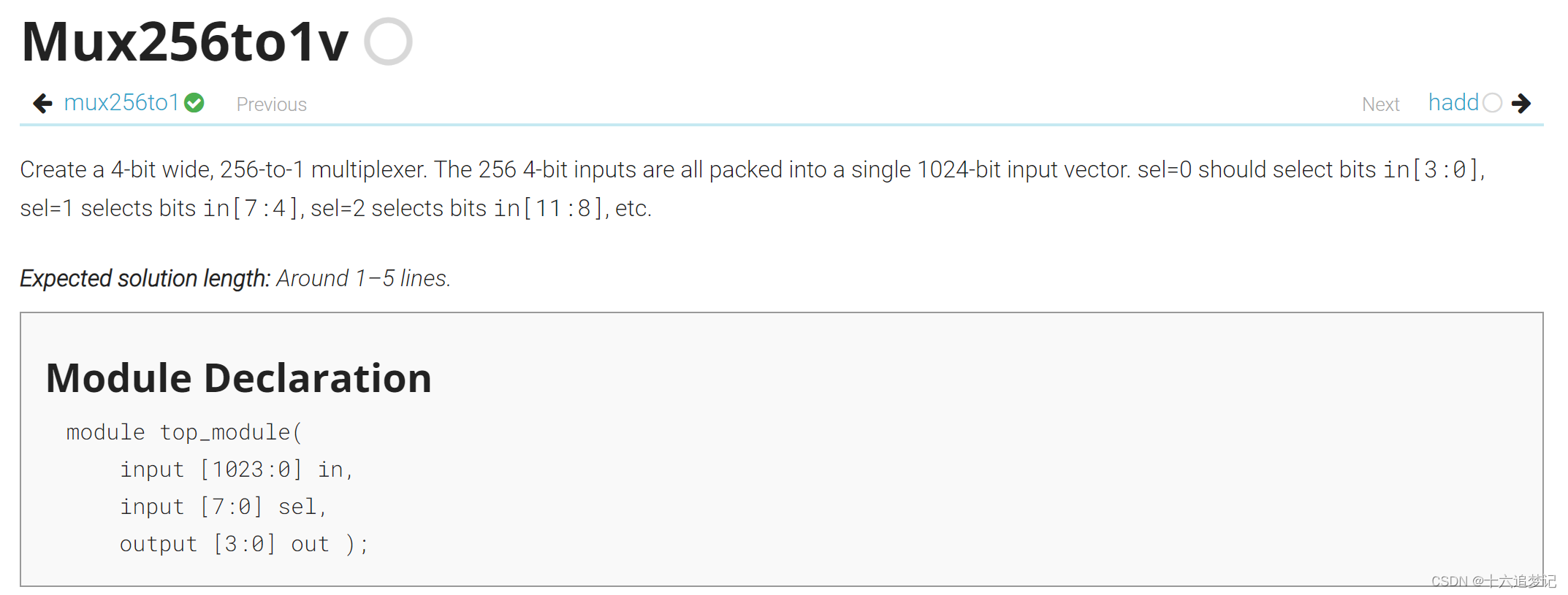
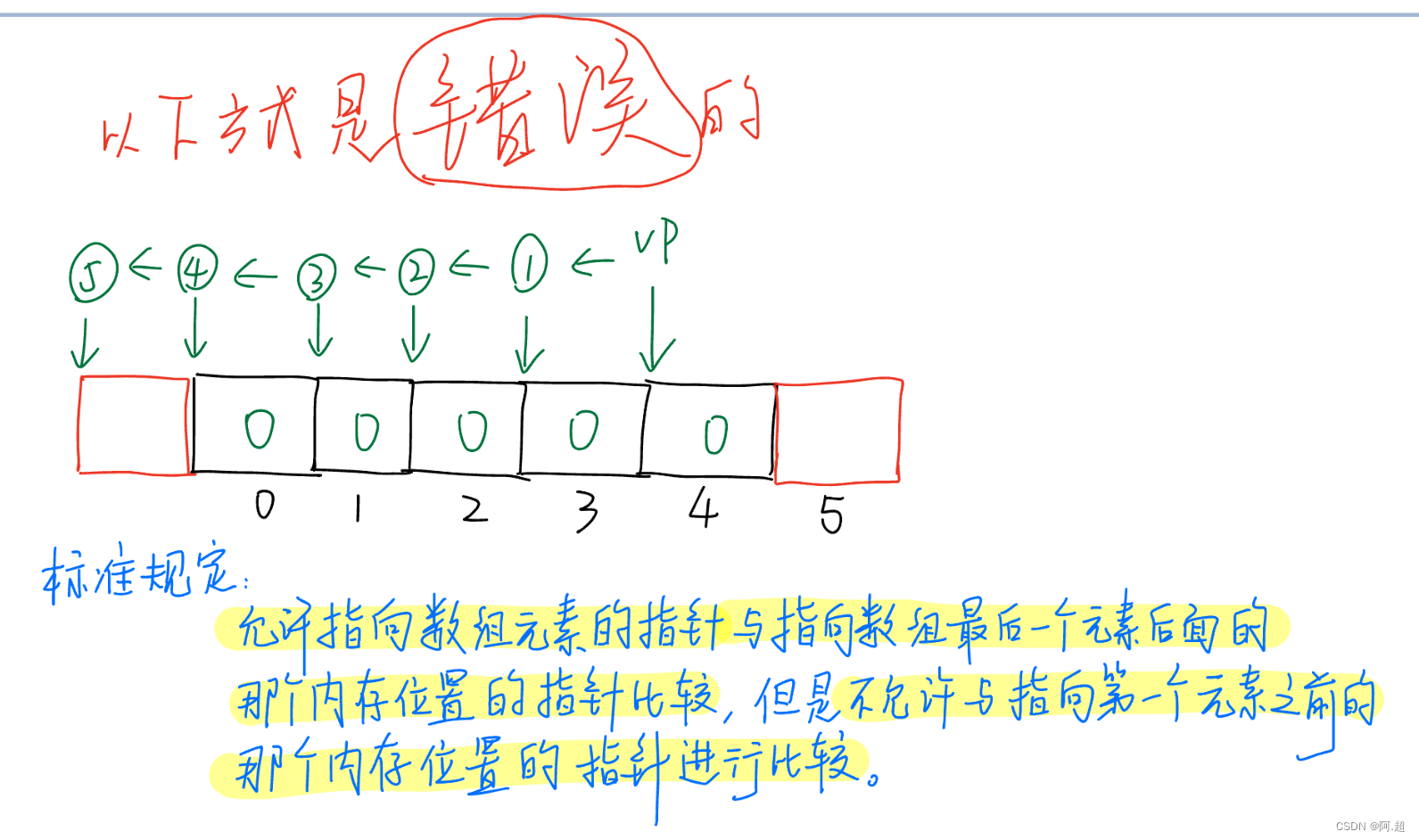
插入排序的基本思想是： 每次将一个待排序的记录按其关键字的大小插入到前面已排好序的文件中的适当位置， 直到全部记录插入完为止。

一 简介

插入排序可分为2类

本文介绍 直接插入排序
它的基本操作是： 假设待排充序的记录存储在数组 R[1…n] 中， 在排序过程的某一时刻， R被划分成两个子区间， R[1…i-1] 和 R[i…n], 其中前一个为已排序的有序区， 后一个为无序区， 开始时有序区中只含有一个元素 R[1], 无序区为 R[2…n] .

排序过程中，只需要每次从无序区中取出第一个元素， 把它插入到有序区的适当位置， 使之成为新的有序区， 依次这样经过 $n-1$ 次插入后， 无序区为空， 有序区中包含了全部 $n$ 个元素， 至此排序完毕。

以java为例， 看一个demo.

import java.util.Arrays;

/**
 * 2024.2.19
 * 插入排序
 */
public class InsertSort {


    public static void main(String[] args) {

        Integer[] array_ = new Integer[]{30,45,10,30,50};
        System.out.println("初始顺序\n"+ Arrays.toString(array_));
        insertSort(array_);
        System.out.println("最后顺序\n"+Arrays.toString(array_));
    }

    static void insertSort(Integer[] array){

        for(int i=1; i<array.length; i++){    //第0位 独自作为有序数列， 从1开始， 说明第二部分从第二个元素操作
            if(array[i]<array[i-1]){       // 0~ i-1位为有序，  如果当前值 小于 前面一个值
                int temp = array[i];       //将当前值 赋值给 临时变量
                int j = i-1;
                //从第i-1位向前遍历并移位， 直到找到小于第 i 位值停止
                for(; j>=0 && temp < array[j]; j--) {   //j-- 说明是从后面往回走， 然后找插入位置
                    array[j+1] = array[j];      // 将记录后移一位
                }
                array[j+1] = temp;      // 将基准插入到正确位置
            }
        }
    }
}

程序运行结果:

二 原理

直接插入排序算法 有两重循环， 外循环表示要进行 $n-1$趟排序， 内循环表明完成一趟排序所进行的记录间的比较和记录的后移。 在每一趟排序中， 最多可能进行 i 次比较， 移动 $i+1$ 个记录(后循环前后作两次移动)

所以在最坏的情况下(反序) ， 插入排序的关键字之间比较次数和记录移动次数达最大值。

最大比较次数: $C_{max}={\sum }_{i=2}^n=\frac{(n+2)(n-1)}{2}$

最大移动次数: $M_{max}={\sum }_{i=2}^n(i-1)=\frac{(n+4)(n-1)}{2}$

三 时间复杂度和空间复杂度

由上述分析可知， 当原始数组的初始状态不同时， 直接插入排序算法的时间复杂度有很大差别， 最好的情况是数组初始为正序即升序， 此时的时间复杂度为 $O(n)$.

最坏的情况是数组初始状态为反序， 此时的时间复杂度为 $O(n^2)$ .

容易证明该算法的平均时间复杂度也为 $O(n^2)$. 这时因为对当前无序区 $R[\mathrm{2..}i-1](2⩽i⩽n)$, 平均比较次数为 $(i-1)/2$,所以总的比较和移动次数约为 $n(n-1)/4\approx \frac{n^2}{4}$.

该算法的空间复杂度 $S(n)为O(1)$

注意概念: 若排序算法所需要的额外空间相对于输入数据量来说是一个常数， 则称该排序为就地排序。
直接插入排序是一个就地排序。