微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

本节目录
一、线性空间
1、欧几里得距离与空间
2、度量空间
3、赋范空间
4、内积空间
二、正交与正交基
本节内容
一、线性空间
通常,我们生活中所处的空间,指的是三维空间。其实本质上与数学中的空间没太大区别,数学上的空间,是三维空间在概念上的拓展。而线性空间里面所有的概念,均可以在三维空间内找到对应的概念。比如,N维线性空间是一个集合,集合中的每一个元素都是一个N维的矢量,表示x=(x1,x2……xN)。当然矢量中的每一个元素,如果均是实数,那么此空间就是实空间;如果均是复数,那就是复空间。通常将线性空间中的元素称为一个点,把上面的集合称为空间。
1、欧几里得距离与空间
在一个N维的线性空间内,存在两个点x=(x1,x2……xN)和y=(y1,y2……yN),根据空间两点之间的距离公式可得:
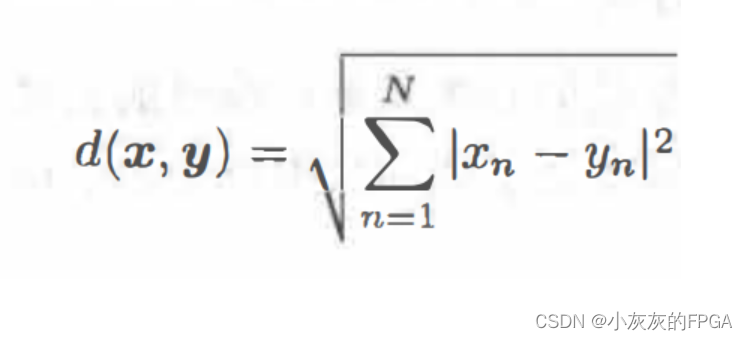
通常将d(x,y)称为欧几里得距离,将定义d(x,y)的线性空间称为欧几里得空间。
2、度量空间
度量的定义:对于一个线性空间V和实数域R,x,y∈V,若d(.,.):V×V→R满足以下三个条件,则称为d(.,.):V×V→R是一个度量。
①非负性:d(x,y)≥0,当且仅当x=y,d(x,y)=0;
②对称性:d(x,y)=d(y,x);
③三角不等式:d(x,y)≤d(x,z)+d(y,z);
d(.,.):V×V→R表示:d是一个函数,将两个属于V的元素作为自变量,值域为R。d本质上从V×V到R的一个映射。
度量空间:定义了度量的线性空间。比如欧式距离空间就是一种最常用的度量空间。
3、赋范空间
范数的定义:
对于一个线性空间V、实数域R、复数域C,x,y∈V,α∈C,若||·||:V→R满足以下三个条件,则称为||·||:V→R是V上的一个范数。
①非负性:||x||≥0,当且仅当x=0,||x||=0;
②齐次性:||αx||=α||x||;
③三角不等式:||x+y||≤||x||+||y||;
范数是一个非负实数,是实数的绝对值的扩展。
4、内积空间
内积的定义:对于一个线性空间V、复数域C,x,y,z∈V,α∈C,若<.,.>:V×V→C满足以下四个条件,则称为<.,.>:V×V→C一个内积。
①正定性:<x,x>≥0,当且仅当x=0,<x,x>=0;
②线性:<x,y+z>=<x,y>+<x,z>;
③线性:<αx,y>=α<x,y>;
④对称性:<x,y>=<y,x>
内积是一个复数。
点积的定义:点积是内积在N维实欧式空间的一种具体形式,V是一个N维实欧式空间,x,y∈V,x=(x1,x2……xN)和y=(y1,y2……yN),则x,y的点积(点乘或标量积)表示如下:

二、正交与正交基
正交的定义:对于一个内积空间V,x,y∈V,若<x,y>=0,那么称x与y正交,即x⊥y。
基,维数,坐标的定义:对于一个内积空间V,e1,e2……,eN∈V,如果V中的任意一个元素x0,均可以唯一地表达为x0=α1e1+α2e2+……+αNeN,将e1,e2……,eN称为V的一组基,线性空间V的维数记作N,α1,α2……,αN是x0在这组基下的坐标。
线性相关和线性无关的定义:对于一个内积空间V,e1,e2……,eN∈V,α1,α2……,αN∈F,如果α1e1+α2e2+……+αNeN=0,能够推导出α1,α2……,αN=0,那么称e1,e2……,eN线性无关,反之,则称e1,e2……,eN线性有关。
标准正交基的定义:对于一个内积空间V,e1,e2……,eN是V的一组基,如果<ei,ej>满足下述关系式,则称e1,e2……,eN是V的一组标准正交基。
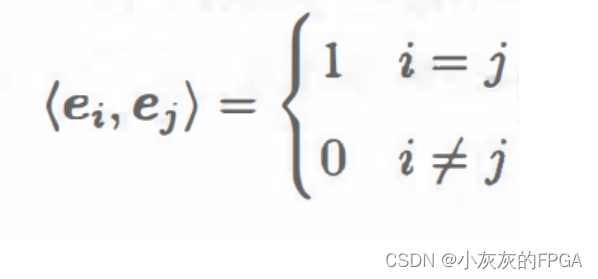






![[WebDav] WebDav基础知识](https://img-blog.csdnimg.cn/direct/a33846ade3ec4793b9769d372f4a2e32.png)