DTL: Disentangled Transfer Learning for Visual Recognition

• 论文链接：https://arxiv.org/pdf/2312.07856.pdf
• 源码链接：https://github.com/heekhero/DTL

简介

大规模预训练加微调的框架已经在各个领域推广。但是由于GPU内存或时间预算的原因，传统的微调可能是难以解决的，因为必须更新整个大模型参数。最近，参数有效迁移学习（PETL）被提出仅更新可训练参数的极小子集。由于其效率和防止过度拟合的能力，PETL的许多变体相继出现。
然而可训练参数的大幅减少并不一定意味着GPU内存使用量同等减少：节省的GPU内存百分比仍然很小（约为25%）。如果由于GPU内存不足而无法对大模型进行微调，即使是PETL框架也可能失败。这个缺点是至关重要的，也是根本性质。因此设计一种有效减少GPU内存使用并充分探索大规模预训练模型效率至关重要。PETL方法的一个共同特征是它们将小型可训练模块与巨大的冻结backbone紧密纠缠。 如LST: Ladder Side-Tuning for parameter and memory efficient transfer learning中所示，为了正确更新特定网络参数，模型必须从激活中缓存相关的中间梯度。这种纠缠设计使缓存称为GPU内存占用的相当大一部分，从而阻碍了大预训练模型在各种任务中应用。
为了解决这个基础缺点，本文提出了纠缠迁移学习（Disentangled Transfer Learning），它通过提出轻量级紧凑侧网络（Compact Side Network，CSN）将权重更新与backbone分离。DTL不仅大大减少了GPU内存占用，也取得了知识迁移的高精度。
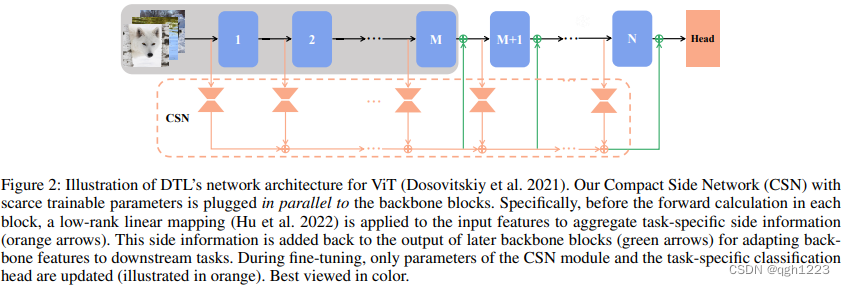
如图2所示，CSN由若干低秩线性映射矩阵以抽取特定任务信息。通过将这些信息注入到后面几个backbone块中，自适应地校准预训练模型生成的部分中间特征，使得这些特征对下游任务更具判别性。本文还可以将DTL增强为DTL+，它插入额外的全局深度可分离卷积（DWConv）层，以在CSN向backbone注入时收集空间信息。DTL非常简单，并且与各种backbone架构兼容。backbone中早期块的输出在微调过程中保持不变，当提供相同输出时可以在多个下游任务中重用backbone特征。

当前PETL方法的限制

假设有N层的FFN网络$y=f_N(f_{N-1}(\dots f_1(x)))$。层i权重矩阵$W_i$偏差项$b_i$。$o_{i+1},z_{i+1}$是层i的输出和激活前特征，满足$o_{i+1}=\sigma (z_{i+1})=\sigma (W_i{o}_i+b_i)$。Ladder Side-Tuning研究显示从损失$L$后向传播到$W_i,b_i$的梯度是：
$$\begin{array}{rl}\frac{\partial L}{\partial W_i}& =\frac{\partial L}{\partial o_{i+1}}{\sigma }_i^{\prime }{o}_i\\ \frac{\partial L}{\partial b_i}& =\frac{\partial L}{\partial o_{i+1}}{\sigma }_i^{\prime }\end{array}$$
其中${\sigma }_i^{\prime }$是$\partial o_{i+1}/\partial z_{i+1}$缩写。进一步$\partial L/\partial o_{i+1}$可以表示为：
$$\frac{\partial L}{\partial o_{i+1}}=\frac{\partial L}{\partial o_{i+2}}\frac{\partial o_{i+2}}{\partial z_{i+2}}\frac{\partial z_{i+2}}{\partial o_{i+1}}=\frac{\partial L}{\partial o_{i+2}}{\sigma }_{i+1}^{\prime }{W}_{i+1}$$
为了正确计算除了模型参数外的参数，在链式规则的对应项 { σ i ′ } \{\sigma_{i}^{\prime}\} {σi′​}需要在微调时被缓存，这支配了GPU内存使用。
本文发现代表性的PETL方法将可训练参数与backbone紧密纠缠在一起，这几乎不会减少缓存 { σ i ′ } \{\sigma_{i}^{\prime}\} {σi′​}中GPU内存使用。这一特性表明，与完全微调相比，即使可训练参数数量非常少，GPU内存占用也无法有效减少。
为了解决这一根本问题，本文提出了一种新的学习范式，称为纠缠迁移学习（Disentangled Transfer Learning，DTL）。DTL核心思想是将小型额外模块权重更新从backbone中分离出来。因此为后向传播存储的${\sigma }_i^{\prime }$能被剧烈减少。通过这种方式，DTL成功地进一步突破了当前PETL的极限，不仅提高了参数效率，而且在微调大规模预训练模型时减少了必要的GPU内存大小。
本文提出了一种简单且有效的方法正确微调大规模预训练模型。为了平衡不同环境中的识别精度和架构复杂性，本文引入了两种变体DTL和DTL+。

DTL

首先给出最简单的形式。图2给出了ViT架构对应的提出模块框架，这主要由紧凑边网络（Compact Side Network，CSN）组成。CSN被插入到backbone中用于信息聚合和特征自适应。提出的方法与其他类型的ViT兼容。
给定包含N块的ViT backbone，前向计算可以描述为$z=b_N(b_{N-1}(\dots b_1(x)))$。$z$是输出令牌。$z_{i+1}$是块$b_i$输出$z_{i+1}=b_i(z_i)$，$z_1=x$。本文CSN由N个低秩线性变换矩阵组成，每个插入到一个块中以提取特定于任务的信息。记$w_i=a_i{c}_i$是第i块的权重矩阵。其中$a_i\in {\mathbb{R}}^{d\times d^{\prime }},c_i\in {\mathbb{R}}^{d^{\prime }\times d}$且$d^{\prime }\ll d$。CSN逐渐从每个块聚集信息：
$$\begin{array}{rl}{h}_{i+1}& =h_i+z_i{w}_i\\ z_{i+1}& =b_i(z_i)\end{array}$$
$h_i$是CSN的第i层输出，$h_1=0$。在这之后，从$M$块开始，聚合的特定于任务的信息$h_{i+1}$用于通过将$z_{i+1}$添加回$z_{i+1}$来使其适应下游任务。因此当$i\ge M$时满足
$$z_{i+1}^{\prime }=z_{i+1}+\theta (h_{i+1})$$
$z_{i+1}^{\prime }$是$b_i$的适应输出。$\theta (x)$是swish激活函数。为了防止$z_{i+1}^{\prime }$在微调开始时急剧偏离$z_{i+1}$，${\alpha }_i$遵循均匀分布初始化，$c_i$是零初始化。第i块的输出可以表示为：
$$z_{i+1}^{\prime }=\{\begin{array}{ll}{z}_{i+1}+\theta \left(h_{i+1}\right)& \text{ if }i\ge M\\ z_{i+1}& \text{ otherwise }\end{array}$$
本文发现小的$d^{\prime }$表现得相当好，这表明backbone特征具有高度冗余性。除了保持$d^{\prime }$较小之外，在Swish中使用较大的$\beta$来进一步减少冗余。

DTL+

为了进一步加强本文方法的有效性，在应用$\theta$之后，本文将一个额外的全局深度可分离卷积（Depthwise Separable Convolution，DWConv）层$g$附加到每个侧层。DTL+公式可以描述为：
$$z_{i+1}^{\prime }=\{\begin{array}{ll}{z}_{i+1}+g(\theta \left(h_{i+1}\right))& \text{ if }i\ge M\\ z_{i+1}& \text{ otherwise }\end{array}$$
$g$步幅设置为1，零填充用于确保不改变特征尺寸。$g$在不同CSN层间共享，使得g中的可训练参数数量与初始CSN相比是小的并且整个CSN模块仍然是轻量级的。