好久不见,甚是想念,最近一直在看过河这道题(感觉最近脑子有点宕机QAQ),现在算是有点懂了,打算记录下这道又爱又恨的题。(如有错误欢迎大佬帮忙指出)
话不多说,直接看题:

类比分组背包,我们可以令f[i][j]表示前i个数能否组成j.
转移方程为:f[i][j]=f[i-1][j-x1^2]||f[i-1][j-x2^2]||....||f[i-1][j-xi^2]
现在我们考虑优化一下:
因为f[i][j]为bool类型,我们可以尝试用bitset优化一下。
我们每一行用bitset,然后用位运算实现(比正常平移优化约32倍)
f[i]=f[i-1]||f[i-1]<<(x[i]^2);(注意bitset最低位在最右边)
下面为AC代码:
#include<bits/stdc++.h>
using namespace std;
int n;
bitset<1000100> f[110];
int main(){
cin>>n;
f[0][0]=1;
for(int i=1;i<=n;i++){
int l,r;
scanf("%d%d",&l,&r);
for(int k=l;k<=r;k++){
f[i]|=f[i-1]<<(k*k);
}
}
cout<<f[n].count();
}接题:

类似爬楼梯,我们记f[i]为到i时最少踩的个数。如果,f[i]上有石子,那么f[i]=min(f[i-j])+1(j>=s&&j<=t).然后一看范围,空间与时间都不允许。
我们应该还记得上次背包用map存的情况,这是因为空间上有大量的冗余。
而在这一题上,我们发现相比于桥,石子特别小,也说明他们间的距离非常大.
于是我们进行状态压缩。
从这开始就困了我蛮久(还是自己太菜了QAQ)
首先按照上述过程我们顺利过了30,我们不妨先用自己测试输出一下具体的样子。
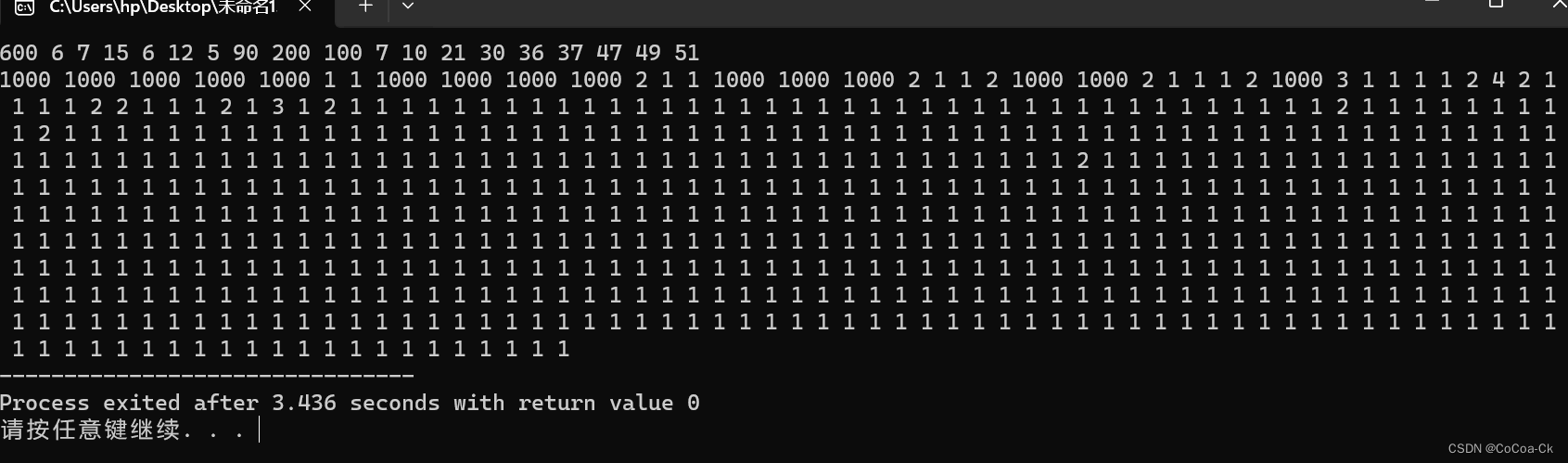
我们发现如果两个石子距离十分大,从某一个位置开始,dp的值都一样。
比赛时,直接压缩成一个不超范围的直接提交(如果是我的话,就直接赋一个2024)
当然,虽然规律很明显,但对于有”强迫症“的我来说还是有点难以接受,于是我们从感性与严格证明的角度来论证正确性。
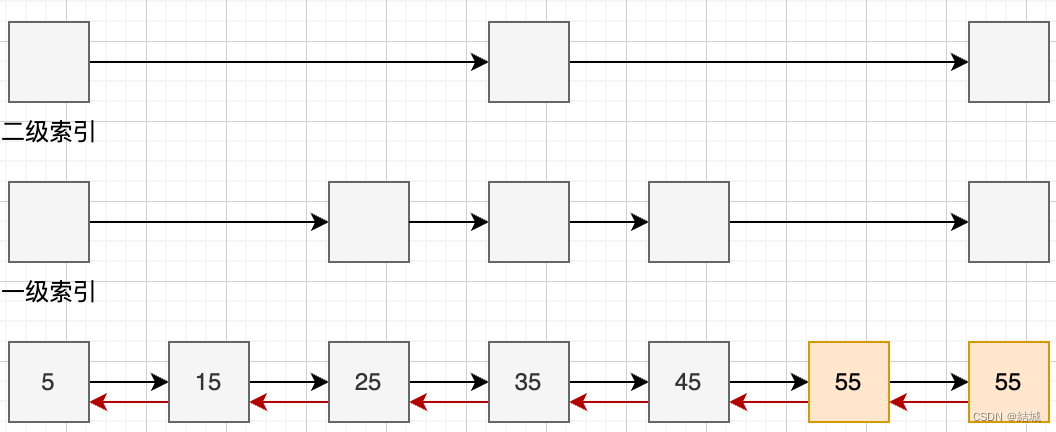
我们不妨自己先画个数轴,我们以6/7举例。

很显然,越到后面,每一段逐渐重合,然后就连续了,因为没有石子,假设某一段的dp值不同(假设有3个不同的值),那么到了后面,对于每一个点,他的状态势必是在<=3个的不同的值里选min的,而3个不同的值中势必有最小的一个,越到后面,除了最小的其他2个一定会在过程中慢慢被舍弃,最终收敛于最小的值(当然,可能有无法到达的)。
总结一下,当两个石子离得比较远,那在中间的这一段,其实就是在经过上一个石子的更新后去不断地筛选出min然后就不变了,而我们要做的就是把不变的一段删掉)
可能有点抽象,那么我们来严格证一下:
首先,我们得知道一个结论:
在离一点oS(S−1)的位置其每一点都可以到(等会证)
然后请看分析:

因此,我们推出一个结论:
在离一点oS(S−1)的位置其每一点都可以到并且他们的dp值都一样。
接下来,我们就得到了压缩方法:
如果两个石子距离>s(s-1),那么就把他变成s(s-1),这样就可以顺利通过了(注意,虽然这样石子后面的几个位置可能不准确,但是不妨碍求min的正确性,保险一点,可以再多空格,这样子每一个点的dp都是对的了)。
下面是对那个数学结论的证明:
我看网上很多是用Bezout's identity来证,我在这采用比较直观的方法(这里证s^2,比较粗略):

下面给出AC代码(注意s==t的情况):
#include<bits/stdc++.h>
using namespace std;
int l,s,t,m,ck[110],dp[100000],ze[110];
map<int,int> mp;
bool cmp(int a,int b){
return a<b;
}
int main(){
cin>>l>>s>>t>>m;
memset(dp,0x3f,sizeof(dp));
for(int i=1;i<=m;i++) scanf("%d",&ck[i]);
if(s==t){
int cnt=0;
for(int i=1;i<=m;i++){
if(ck[i]%s==0) cnt++;
}
cout<<cnt;
return 0;
}
sort(ck+1,ck+m+1,cmp);
int mm=s*s+10;
ze[0]=0;
for(int i=1;i<=m;i++){
ze[i]=min(mm,ck[i]-ck[i-1])+ze[i-1];
mp[ze[i]]=1;
}
ze[m+1]=min(mm,l-ck[m])+ze[m];
dp[0]=0;
for(int i=1;i<=ze[m+1]+t-1;i++){
for(int j=s;j<=t;j++){
if(i-j>=0){
if(mp.count(i)==1) dp[i]=min(dp[i],1+dp[i-j]);
else dp[i]=min(dp[i],dp[i-j]);
}
}
}
int ans=1000;
for(int i=ze[m+1];i<=ze[m+1]+t-1;i++) ans=min(ans,dp[i]);
cout<<ans;
}