二分图首先是个无向图。
主要有以下几类问题:
1.二分图,不存在奇数环,染色法不存在矛盾
2.匈牙利算法,匹配,最大匹配,匹配点,增广路径
3.最小点覆盖,最大独立集,最小路径点覆盖,最小路径重复点覆盖
最大匹配数=最小点覆盖=总点数-最大独立集=总点数-最小路径覆盖
(以下两种一般不用二分图来写)
4.最优匹配(达到最大匹配的情况下,边权和的最大值),KM算法(最小费用流)
5.多重匹配(每个点可以匹配多个点)(最大流)
1.二分图 = 不存在奇数环 = 染色法不存在矛盾
证明比较简单,可以自行搜索。
染色法模板:
bool dfs(int u, int c)
{
color[u] = c;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (color[j])//如果j已经染色,判断是否有矛盾
{
if (color[j] == c) return false;//如果有矛盾那么判否
}
else //如果没有染色,那么对j染色,判断往下染的时候是否会出现矛盾
{
if (dfs(j, 3 - c)) return false;
}
}
return true;
}
257. 关押罪犯(257. 关押罪犯 - AcWing题库)


思路:首先我们注意到,需要将所有罪犯分到两个监狱中去,那么联想到二分图,二分图的要求就是边全部在两个集合之间,集合内部没有边,但是这里显然不能保证图是符合要求的,但是我们要求的是最大值最小,所以考虑二分,对于一个二分值,如果小于等于这个二分值的可以分进一个监狱,否则就必须分进两个监狱,那么从二分图的角度来看,相当于只保留了大于二分值的边。那么我们只需要判断这些被保留的边是否可以构成一个二分图,就可以判断当前的二分值是否有效了。如果可以构成二分图,显然这么分是可以的,如果不能构成二分图,那么就需要将二分值往上调一调,因为这样的话留下的边就更少了,产生矛盾的概率也更小了。
#include<bits/stdc++.h>
using namespace std;
const int N=20010,M=200010;
int h[N],e[M],ne[M],w[M],idx;
int n,m;
int color[N];
void add(int a,int b,int c)
{
w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool dfs(int u,int c,int mid)
{
color[u]=c;
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
if(w[i]<=mid) continue;
if(color[j])
{
if(color[j]==c) return 0;
}
else
{
if(!dfs(j,3-c,mid)) return 0;
}
}
return 1;
}
bool check(int mid)
{
memset(color,0,sizeof color);
for(int i=1;i<=n;i++)
{
if(!color[i])
{
if(!dfs(i,1,mid)) return 0;
}
}
return 1;
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c),add(b,a,c);
}
int l=0,r=1e9;
while(l<r)
{
int mid=(l+r)/2;
if(check(mid)) r=mid;
else l=mid+1;
}
cout<<l;
}2.匈牙利算法,匹配,最大匹配,匹配点,增广路径
匈牙利算法就是从二分图中查找最大匹配的算法。
匹配指二分图中一组没有公共点的边;
最大匹配是指边的数量最多的一组匹配
匹配点指的是在匹配中的点
增广路径:从一个非匹配点沿着非匹配边、匹配边、非匹配边、匹配边、...,最后走到另一个集合中的一个非匹配点。得到的路径是一个增广路径。增广路径是可以取代当前的匹配。
最大匹配等价于不存在增广路径
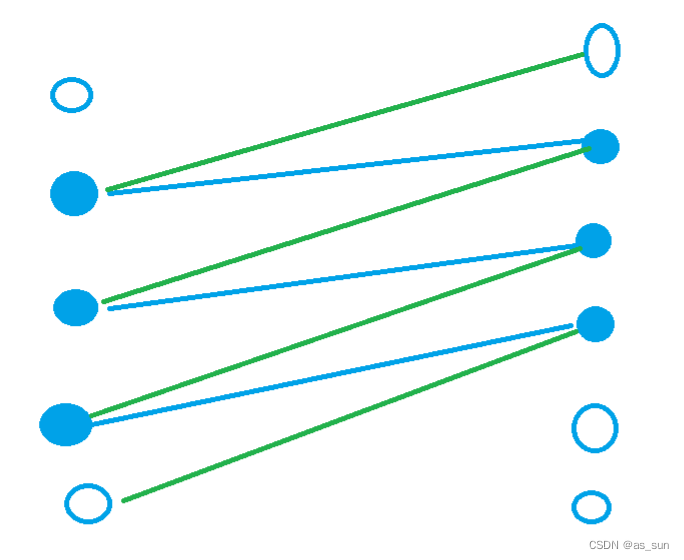
找最大匹配用的是匈牙利算法,时间复杂度最坏O(nm),但一般不会到这个值。
匈牙利算法的实现思路是:遍历一个点集中的每个点,为每个点找一个匹配,如果找到的点还没有被匹配过,那么就将找到的点的匹配记为当前点,否则就去看能否为这个点的匹配点找一个新的匹配,注意新的匹配不能是这个点,所以在搜到这个点的时候需要标记以下。每一次开始查找的时候所有点都是没有标记的,标记只是在这一轮查找中这个点不能用,但是下一轮就可以用了。因为从一个点集找,所以我们建单向边即可。
861. 二分图的最大匹配(活动 - AcWing)

#include<bits/stdc++.h>
using namespace std;
const int N=1010,M=100010;
int n1,n2,m;
int h[N],e[M],ne[M],idx;
int st[M],match[M];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool find(int u)
{
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
if(st[j]) continue;
st[j]=1;
if(!match[j]||find(match[j]))
{
match[j]=u;//这里要记得分配
return 1;
}
}
return 0;
}
int main()
{
scanf("%d%d%d",&n1,&n2,&m);
memset(h,-1,sizeof h);
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
}
int c=0;
for(int i=1;i<=n1;i++)
{
memset(st,0,sizeof st);
if(find(i)) c++;
}
cout<<c;
}372. 棋盘覆盖(活动 - AcWing)

思路:这里可能会想到用状态压缩来做,但是N太大了,2^100,一定会超时。所以我们需要换个思路。
这题其实有个特别巧妙地地方,我们将横纵坐标之和为奇数地称为奇点,为偶数的称为偶点,仔细观察可以放的位置,占据的都是连续的两个点,或横或竖,也就是一个奇点一个偶点,再加上不能重复,那么不就是在奇点和偶点两个集合之间找最大匹配嘛,分析到这里就很简单了,我们从奇点集去找偶点集的匹配即可。
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int,int> pii;
const int N=120;
int n,m;
pii match[N][N];
int g[N][N],st[N][N];
int dx[]={0,0,-1,1};
int dy[]={1,-1,0,0};
bool find(int x,int y)
{
for(int u=0;u<4;u++)
{
int a=x+dx[u],b=y+dy[u];
if(a<=0||a>n||b<=0||b>n) continue;
if(g[a][b]||st[a][b]) continue;
st[a][b]=1;
pii t=match[a][b];
if(t.x==-1||find(t.x,t.y))
{
match[a][b]={x,y};
return 1;
}
}
return 0;
}
int main()
{
scanf("%d%d",&n,&m);
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
g[a][b]=1;
}
memset(match,-1,sizeof match);
int c=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if((i+j)%2==0 || g[i][j]) continue;
memset(st,0,sizeof st);
if(find(i,j)) c++;
}
}
cout<<c;
}3.最小点覆盖,最大独立集,最小路径点覆盖,最小路径重复点覆盖
结论:最大匹配数=最小点覆盖=总点数-最大独立集=总点数-最小路径覆盖
最小点覆盖:选出最少的点,使得每条边的两个端点中至少有一个点被选出来了。
376. 机器任务(376. 机器任务 - AcWing题库)


思路:每个任务有两种完成的方式,那么如果在两种方式之间连一条边,那么就会得到一个二分图,相当于要求这个二分图的最小点覆盖。因为任意一条边至少有一个端点要被选。
对了要注意一下,初始为0,所以如果a或者b为0的话,可以直接执行,不用算到后面重启中去。
#include<bits/stdc++.h>
using namespace std;
const int N=120,M=1010;
int n,m,k;
int h[N],e[M],ne[M],idx;
int st[N],match[N];
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool find(int u)
{
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
if(st[j]) continue;
st[j]=1;
if(match[j]==-1||find(match[j]))
{
match[j]=u;
return 1;
}
}
return 0;
}
int main()
{
while(~scanf("%d",&n))
{
if(!n) break;
scanf("%d%d",&m,&k);
memset(h,-1,sizeof h);
memset(match,-1,sizeof match);
while(k--)
{
int c,a,b;
scanf("%d%d%d",&c,&a,&b);
if(!a||!b) continue;//最初为0
add(a,b);
}
int c=0;
for(int i=1;i<=n;i++)
{
memset(st,0,sizeof st);
if(find(i))c++;
}
printf("%d\n",c);
}
}最大独立集:从图中选出最多的点,使得任意两点之间没有边
最大团:从图中选出最多的点,使得任意两点之间都有边
在二分图中,求最大独立集 => 去掉最少的点将所有边都覆盖点 <=> 最小点覆盖 <=> 最大匹配
最大独立集=n-最大匹配
378. 骑士放置(378. 骑士放置 - AcWing题库)

这里不能互相攻击到,那么我们将可以互相攻击的点之间连边,得到一张图,那么需要求的就是最大独立集,因为选出的点两两之间没有边。然后还需要确定的一个问题就是这张图是否是二分图。对于一个点,它能攻击到的点与它的横纵左边之间的总差值应该是一个奇数,那么就会改变奇偶性,那么我们按照奇点偶点分成两个集合,那么就是一个二分图。类似于棋盘覆盖那道题,问题就解决了。
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int,int> pii;
const int N=120;
int n,m,t;
pii match[N][N];
int g[N][N],st[N][N];
int dx[]={1,1,-1,-1,2,2,-2,-2};
int dy[]={2,-2,2,-2,1,-1,1,-1};
bool find(int x,int y)
{
for(int u=0;u<8;u++)
{
int a=x+dx[u],b=y+dy[u];
if(a<1||a>n||b<1||b>m) continue;
if(g[a][b]||st[a][b]) continue;
st[a][b]=1;
pii t=match[a][b];
if(t.x==-1||find(t.x,t.y))
{
match[a][b]={x,y};
return 1;
}
}
return 0;
}
int main()
{
scanf("%d%d%d",&n,&m,&t);
for(int i=1;i<=t;i++)
{
int a,b;
scanf("%d%d",&a,&b);
g[a][b]=1;
}
memset(match,-1,sizeof match);
int c=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if((i+j)%2 || g[i][j]) continue;
memset(st,0,sizeof st);
if(find(i,j)) c++;
}
}
cout<<n*m-t-c;//坏点是不能被选的,所以不包含在图中,我们是要从图中选点,图中的总点数-最大匹配数
}最小(路径)点覆盖:在DAG(有向无环图)中用最少的互不相交(点边都不重复)的路径将所有点覆盖住。
这里需要用到拆点:对于原来的每个点建立一个新点,原点作为出点,新点作为入点。那么相当于就产生一个二分图。那么最小点覆盖=n(一边的点数)-m(最大匹配数)
因为互不相交,所以每个点只有一个出度和一个入度,那么在新图中就对应一个匹配。
路径的终点对应左侧一个非匹配点,那么一个非匹配点就对应一条路径。
所以求最小路径数,就是求左侧最少非匹配点的数量,那么匹配点最多,那么就是最大匹配。
如果可以相交,那么就是最小路径重复点覆盖。
求原有向图的传递闭包得到一个新图,求新图的最小路径点覆盖。
379. 捉迷藏(379. 捉迷藏 - AcWing题库)

相当于给定一个有向无环图,从中选出一些点,使得任意两点之间都不能从一个走到另一个。
我们假设图中有m个最小路径重复点覆盖,那么显然我们只能在一条路径上选一个点,否则选的点就是可达的。因为这里只要可达就可以相互看到,所以需要求最小路径重复点覆盖。
传递闭包可以用Floyd算法来求。
#include<bits/stdc++.h>
using namespace std;
const int N=210;
int n,m;
int st[N],g[N][N],match[N];
int find(int u)
{
for(int i=1;i<=n;i++)
{
if(g[u][i]==0) continue;
if(st[i]) continue;
st[i]=1;
if(!match[i]||find(match[i]))
{
match[i]=u;
return 1;
}
}
return 0;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
g[a][b]=1;
}
for(int k=1;k<=n;k++)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
g[i][j]|= g[i][k]&g[k][j];
}
}
}
int res=0;
for(int i=1;i<=n;i++)
{
memset(st,0,sizeof st);
if(find(i)) res++;
}
cout<<n-res;
}