目录

LintCode 炼码完全背包问题

 【解法一】

【解法二】

---

完全背包问题

 【解法一】

解释： 第一个for循环表示从第一个物品开始遍历

            第二个for循环表示逆向 从背包容量为m时开始处理（滚动数组）

            第三个for循环表示装入k个该物品，装一个为下限，也可以为0

                           最多装入数为 容量j除以该物品重量（即为for循环上限）

            状态转移方程为在0-1背包问题上多了一次循环判断装第i个物品的个数

class Solution {
public:
    int backPackIII(vector<int> &a, vector<int> &v, int m) {
        // write your code here
        int n = a.size();
        vector<int> dp(m+1);
        for(int i = 0; i < n; i++)
            for(int j = m; j >= a[i]; j--)
                for(int k = 1; k <= j/a[i]; k++)
                    dp[j] = max(dp[j], (dp[j-k*a[i]] + k*v[i]));
        return dp[m];
    }
};

【解法二】

状态转移方程的推导：

对于完全背包，当j处于3的位置，3可以装入1个A物品，也就是（1,3）位置，只有1价值

                        也可以不装A，也就是在j=0的条件下装入一个B，达到3的价值

对于完全背包，当j处于6的位置，6可以装入3个A物品，也就是dp[i-1][j]，但只有3的价值

                        也可以在装入一件B物品的条件下再继续装入一个B物品，达到了6的价值

通过上面俩个例子发现，（i，j）位置元素是在（i-1，j）和（i，j-w[i]+c[i]）中取一个最大值

                        也就是在本行数据和上一行数据中选出一个最大值，那么应用到滚动数组思想，

                        dp[j] = max(dp[j], dp[j-w[i]]+c[i])                       

                        对应于0-1背包时从后往前更新元素，这里采用从前往后进行更新元素。

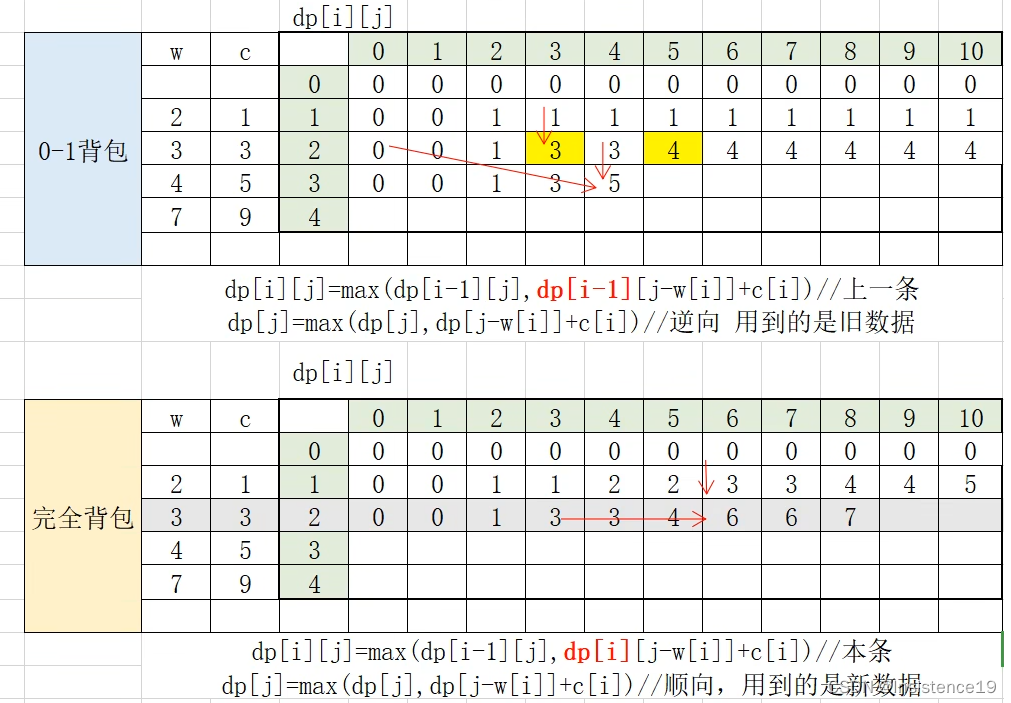
对照上图完全背包的推导过程，写出状态转移方程

即完全背包采用滚动数组思想后与0-1背包的转移方程为同一个，只是推导的顺序不同

第二层for循环，从j能够装入第i件物品的位置开始进行遍历

class Solution {
public:
    int backPackIII(vector<int> &a, vector<int> &v, int m) {
        // write your code here
        int n = a.size();
        vector<int> dp(m+1);
        for(int i = 0; i < n; i++)
            for(int j = a[i]; j <= m; j++)
                dp[j] = max(dp[j], (dp[j-a[i]] + v[i]));
        return dp[m];
    }
};