1.1基本思想

把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列 。实际中我们玩扑克牌时，就用了插入排序的思想。

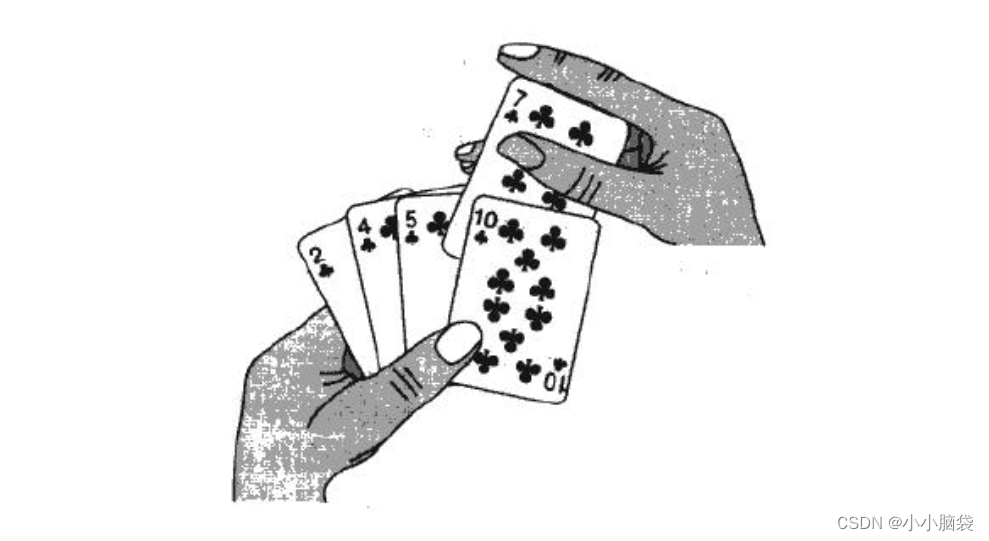
1.2动态图示感知

1.3静态图示详解

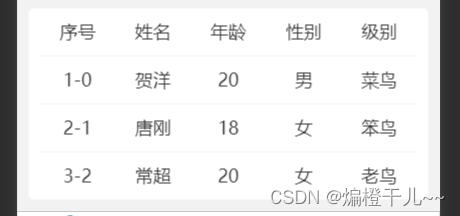
以一组待排序数据：5 3 1 6 9 9为例：

1.4代码实现

   public static void insertSort(int[] array){
        for(int i = 1;i < array.length;i++){
            int tmp = array[i];//初始化tmp的值
            int j = i - 1;
            for( ;j >= 0;j--){
                //这里带不带等号，会影响排序的稳定性
                if(array[j] > tmp){
                    array[j+1] = array[j];
                }else{
                    break;
                }
            }
            array[j + 1] = tmp;
        }
    }

1.5时间复杂度

1.5.1最好情况

当待排序数组已经是一个升序排列的数组时，此时时间复杂度最低。因为对于i遍历的每一个值，j无需向左遍历，此时只相当于i遍历了一遍数组(确切的说，是遍历了除第一个元素外的数组)，因此时间复杂度为O(n)。

1.5.2最差情况

当待排序数组已经是一个降序排列的数组时，此时时间复杂度最高。因为对于i遍历的每一个值，j需要向左遍历直到-1，因此整个排休的时间复杂度为O(n^2)。

特点：由以上分析可知，待排序的数据越“有序”，直接插入排序算法的时间复杂度越低。这一特点可以用到某些排序算法的优化上，比如快速排序。

1.6空间复杂度

整个排序过程只创建了常数个临时变量，因此空间复杂度为O(1)。

1.7稳定性

在1.2图示详解中，原始数组中的数据9和9，在排序后相对位置没有发生变化，因此直接插入排序是稳定的排序。

1.7.1一个小问题

如果将原有代码中的这句：

if(array[j] > tmp){
    array[j+1] = array[j];
}else{
    break;
}

改为：

if(array[j] >= tmp){
    array[j+1] = array[j];
}else{
   	break;
}

即将判断条件的 “>” 改为 “>=”
原有的直接插入排序还是稳定的吗？
答：不稳定。

图示说明如下(对比1.3静态图示详解的最后两步)：

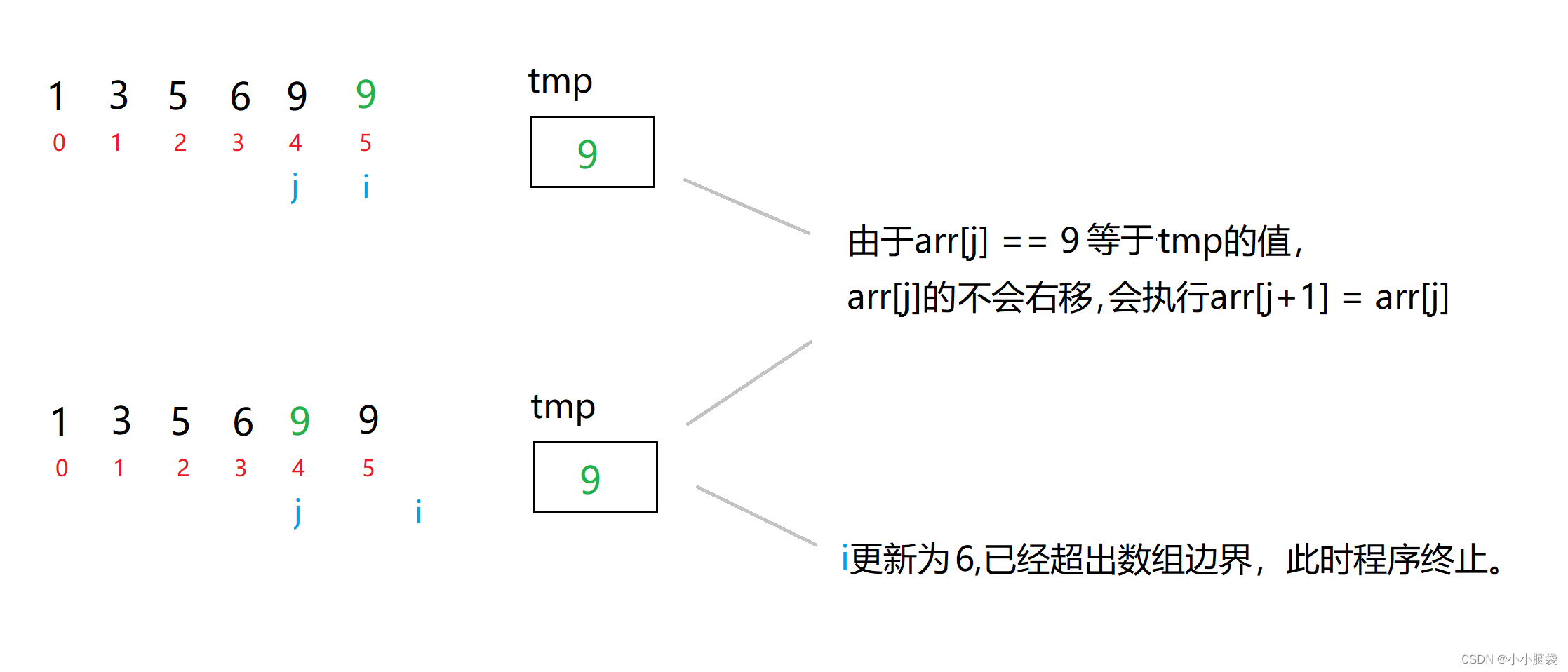
所以直接插入排序是稳定的还是不稳定的呢？
前面已经说明了直接插入排序是稳定的排序。之所以会出现把 > 修改成 >=,原有的排序由稳定变为不稳定的情况，是因为：一个本身就不稳定的排序，是不可能是现成稳定的排序的；而一个本身稳定的排序，是可以实现为不稳定的排序的。