输入一个 n
行 m
列的整数矩阵，再输入 q
个操作，每个操作包含五个整数 x1,y1,x2,y2,c
，其中 (x1,y1)
和 (x2,y2)
表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c
。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数 n,m,q
。

接下来 n
行，每行包含 m
个整数，表示整数矩阵。

接下来 q
行，每行包含 5
个整数 x1,y1,x2,y2,c
，表示一个操作。

输出格式
共 n
行，每行 m
个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000
,
1≤q≤100000
,
1≤x1≤x2≤n
,
1≤y1≤y2≤m
,
−1000≤c≤1000
,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2

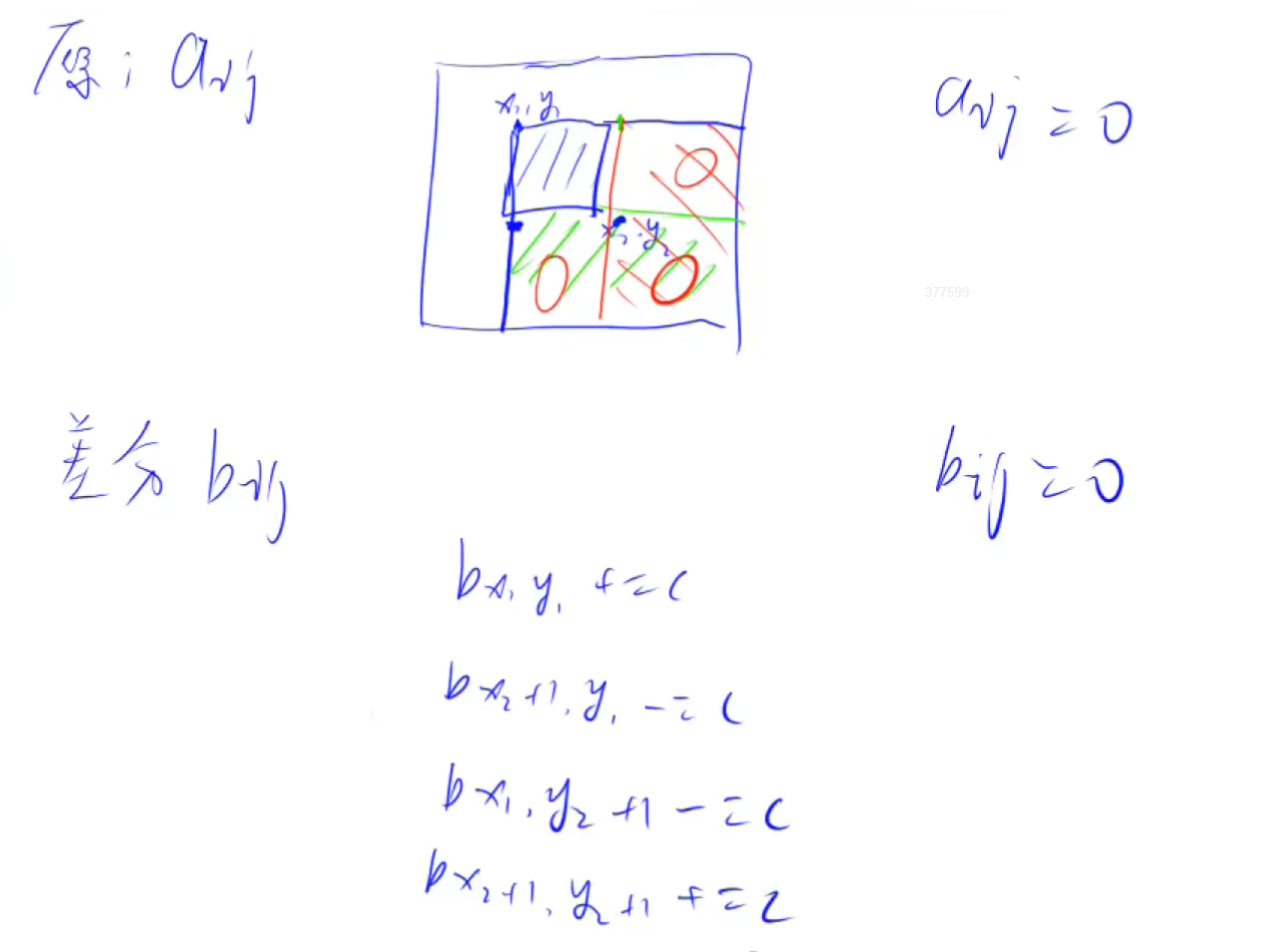
需要注意的是，更新的方式。根据图会更容易理解和记住。

#include <iostream>

using namespace std;

const int N = 1010;
int n, m, q;
int a[N][N], b[N][N];

int main ()
{
    scanf("%d%d%d", &n, &m, &q);
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);
            
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ ) // 初始化差分矩阵，相当于把原始矩阵a的每个元素插进去
        {
            b[i][j] += a[i][j];
            b[i + 1][j] -= a[i][j];
            b[i][j + 1] -= a[i][j];
            b[i + 1][j + 1] += a[i][j];
        }
    
    while(q -- ) // 插入操作
    {
        int x1, y1, x2, y2, c;
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
        b[x1][y1] += c;
        b[x2 + 1][y1] -= c;
        b[x1][y2 + 1] -= c;
        b[x2 + 1][y2 + 1] += c;
    }
    
    for(int i = 1; i <= n; i ++ ) // 求前缀和
        for(int j = 1; j <= m; j ++ )
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
    
    for(int i = 1; i <= n; i ++ )
    {
        for(int j = 1; j <= m; j ++ )
            printf("%d ", b[i][j]);
        printf("\n");
    }
    
    return 0;
}