目录
无权图的单源最短路问题:
1. 迷宫中离入口最近的出口(中等)
2. 最小基因变化(中等)
3. 单词接龙(困难)
4. 为高尔夫比赛砍树(困难)
无权图的多源最短路问题:
1. 01矩阵(中等)
2. 地图中的最高点(中等)
3. 地图分析(中等)
无权图的单源最短路问题:
使用单源BFS可以求解无权图的单源最短路问题,这是由BFS总是按照距离由近到远来遍历图中每个顶点的性质决定的。
1. 迷宫中离入口最近的出口(中等)
class Solution {
public:
int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {
int m = maze.size();
int n = maze[0].size();
vector<vector<bool>> visited(m, vector<bool>(n));
int ans = 0;
// 坐标上下左右的偏移量
int dr[4] = { -1,1,0,0 };
int dc[4] = { 0,0,-1,1 };
queue<pair<int, int>> q;
// 起始坐标入队并标记
q.push({entrance[0], entrance[1]});
visited[entrance[0]][entrance[1]] = true;
while (!q.empty())
{
// 要向外拓展一层,步数++
ans++;
int count = q.size(); // 本层坐标点的个数
for (int i = 0; i < count; i++)
{
// 队头出队
auto [row, col] = q.front();
q.pop();
// 判断刚才出队的坐标上下左右是否满足条件,再判断是否到达出口,到达则直接返回,没到达则入队并标记
for (int j = 0; j < 4; j++)
{
int r = row + dr[j];
int c = col + dc[j];
if (r >= 0 && r < m && c >= 0 && c < n && maze[r][c] == '.' && !visited[r][c])
{
if (r == 0 || r == m - 1 || c == 0 || c == n - 1) // 到达出口
return ans;
q.push({r, c});
visited[r][c] = true;
}
}
}
}
return -1;
}
};2. 最小基因变化(中等)
将距离为1(变化了一个字符)的字符串连接起来构成一个无权图,求start到end的最短路。
class Solution {
public:
int minMutation(string startGene, string endGene, vector<string>& bank) {
unordered_set<string> hash(bank.begin(), bank.end()); // 哈希表记录基因库中的字符串
unordered_set<string> visited; // 标记字符串是否被访问过
string change = "ACGT";
if (startGene == endGene)
return 0;
if (!hash.count(endGene))
return -1;
int ans = 0;
queue<string> q;
// 起始字符串入队并标记
q.push(startGene);
visited.insert(startGene);
while (!q.empty())
{
// 要向外拓展一层,步数++
ans++;
int count = q.size(); // 本层字符串的个数
for (int i = 0; i < count; i++)
{
// 队头出队
string cur = q.front();
q.pop();
// 判断刚才出队的字符串只改变一个字符后是否满足条件,再判断是否到达end,到达则直接返回,没到达则入队并标记
for (int i = 0; i < 8; i++)
{
string tmp = cur;
for (int j = 0; j < 4; j++)
{
tmp[i] = change[j];
if (hash.count(tmp) && !visited.count(tmp))
{
if (tmp == endGene) // 到达end
return ans;
q.push(tmp);
visited.insert(tmp);
}
}
}
}
}
return -1;
}
};3. 单词接龙(困难)
和上一题“最小基因变化”类似,区别是上一题求步数,本题求最短路的顶点数。
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
unordered_set<string> hash(wordList.begin(), wordList.end()); // 哈希表记录字典中的单词
unordered_set<string> visited; // 标记单词是否被访问过
if (!hash.count(endWord))
return 0;
int ans = 1;
queue<string> q;
// 起始单词入队并标记
q.push(beginWord);
visited.insert(beginWord);
while (!q.empty())
{
// 要向外拓展一层,顶点数++
ans++;
int count = q.size(); // 本层单词的个数
for (int i = 0; i < count; i++)
{
// 队头出队
string cur = q.front();
q.pop();
// 判断刚才出队的单词只改变一个字符后是否满足条件,再判断是否到达end,到达则直接返回,没到达则入队并标记
for (int i = 0; i < cur.size(); i++)
{
string tmp = cur;
for (char ch = 'a'; ch <= 'z'; ch++)
{
tmp[i] = ch;
if (hash.count(tmp) && !visited.count(tmp))
{
if (tmp == endWord) // 到达end
return ans;
q.push(tmp);
visited.insert(tmp);
}
}
}
}
}
return 0;
}
};4. 为高尔夫比赛砍树(困难)
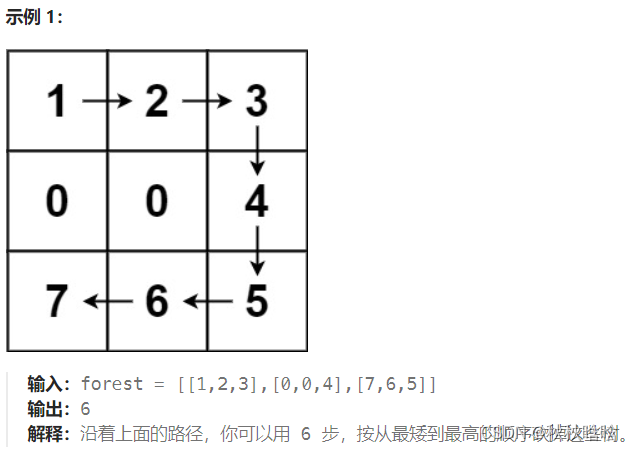
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7
给树按从小到大排序,求顺序相邻的树的最短路。
class Solution {
public:
int cutOffTree(vector<vector<int>>& forest) {
m = forest.size();
n = forest[0].size();
// 给树按从小到大排序,确定砍树的顺序
vector<pair<int, int>> trees;
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (forest[i][j] > 1)
{
trees.push_back({i, j});
}
}
}
sort(trees.begin(), trees.end(), [&](const pair<int, int>& p1, const pair<int, int>& p2)
{
return forest[p1.first][p1.second] < forest[p2.first][p2.second];
});
// 求顺序相邻的树的最短路
int beginr = 0;
int beginc = 0;
int ans = 0;
for (auto& [endr, endc] : trees)
{
int step = bfs(forest, beginr, beginc, endr, endc);
if (step == -1)
return -1;
ans += step;
beginr = endr;
beginc = endc;
}
return ans;
}
private:
int bfs(vector<vector<int>>& forest, int beginr, int beginc, int endr, int endc)
{
if (beginr == endr && beginc == endc)
return 0;
vector<vector<bool>> visited(m, vector<bool>(n)); // 标记坐标是否被访问过
int ans = 0;
queue<pair<int, int>> q;
// 起始坐标入队并标记
q.push({beginr, beginc});
visited[beginr][beginc] = true;
while (!q.empty())
{
// 要向外拓展一层,步数++
ans++;
int count = q.size(); // 本层坐标点的个数
for (int i = 0; i < count; i++)
{
// 队头出队
auto [row, col] = q.front();
q.pop();
// 判断刚才出队的坐标上下左右是否满足条件,再判断是否到达end,到达则直接返回,没到达则入队并标记
for (int j = 0; j < 4; j++)
{
int r = row + dr[j];
int c = col + dc[j];
if (r >= 0 && r < m && c >= 0 && c < n && forest[r][c] && !visited[r][c])
{
if (r == endr && c == endc) // 到达end
return ans;
q.push({r, c});
visited[r][c] = true;
}
}
}
}
return -1;
}
// 坐标上下左右的偏移量
int dr[4] = { -1,1,0,0 };
int dc[4] = { 0,0,-1,1 };
int m;
int n;
};无权图的多源最短路问题:
使用多源BFS可以求解无权图的多源最短路问题,将所有的源点当成一个“超级源点”,问题就变成了单源最短路问题。
1. 01矩阵(中等)
以所有的0为源点开始BFS。
距离数组dist最开始全部初始化为-1,表示没有被访问过,后续要修改成距离(步数)。所以,首先,我们不用创建visited数组标记坐标有没有被访问过;其次,不用创建step变量记录步数,并且不用计算本层坐标点的个数count,也就是说不用确定坐标点是在第几层。
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int m = mat.size();
int n = mat[0].size();
vector<vector<int>> dist(m, vector<int>(n, -1)); // 全部初始化为-1
// 坐标上下左右的偏移量
int dr[4] = { -1,1,0,0 };
int dc[4] = { 0,0,-1,1 };
queue<pair<int, int>> q;
// 所有的源点入队并修改距离为0
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (mat[i][j] == 0)
{
q.push({i, j});
dist[i][j] = 0;
}
}
}
while (!q.empty())
{
// 队头出队
auto [row, col] = q.front();
q.pop();
// 判断刚才出队的坐标上下左右是否满足条件,满足条件则入队并修改距离
for (int j = 0; j < 4; j++)
{
int r = row + dr[j];
int c = col + dc[j];
if (r >= 0 && r < m && c >= 0 && c < n && dist[r][c] == -1)
{
q.push({r, c});
dist[r][c] = dist[row][col] + 1;
}
}
}
return dist;
}
};2. 地图中的最高点(中等)
水域格子的值是确定的,为0,以所有的0为源点开始BFS,和上一题“01矩阵”一模一样。
class Solution {
public:
vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
int m = isWater.size();
int n = isWater[0].size();
vector<vector<int>> dist(m, vector<int>(n, -1)); // 全部初始化为-1
// 坐标上下左右的偏移量
int dr[4] = { -1,1,0,0 };
int dc[4] = { 0,0,-1,1 };
queue<pair<int, int>> q;
// 所有的源点入队并修改距离为0
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (isWater[i][j] == 1)
{
q.push({i, j});
dist[i][j] = 0;
}
}
}
while (!q.empty())
{
// 队头出队
auto [row, col] = q.front();
q.pop();
// 判断刚才出队的坐标上下左右是否满足条件,满足条件则入队并修改距离
for (int j = 0; j < 4; j++)
{
int r = row + dr[j];
int c = col + dc[j];
if (r >= 0 && r < m && c >= 0 && c < n && dist[r][c] == -1)
{
q.push({r, c});
dist[r][c] = dist[row][col] + 1;
}
}
}
return dist;
}
};3. 地图分析(中等)
以所有的陆地单元格为源点开始BFS,陆地单元格对应在距离数组dist中的值为0,和“01矩阵”、“地图中的最高点”都是一样的题。
class Solution {
public:
int maxDistance(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<vector<int>> dist(m, vector<int>(n, -1)); // 全部初始化为-1
int ans = -1;
// 坐标上下左右的偏移量
int dr[4] = { -1,1,0,0 };
int dc[4] = { 0,0,-1,1 };
queue<pair<int, int>> q;
// 所有的源点入队并修改距离为0
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (grid[i][j] == 1)
{
q.push({i, j});
dist[i][j] = 0;
}
}
}
while (!q.empty())
{
// 队头出队
auto [row, col] = q.front();
q.pop();
// 判断刚才出队的坐标上下左右是否满足条件,满足条件则入队并修改距离
for (int j = 0; j < 4; j++)
{
int r = row + dr[j];
int c = col + dc[j];
if (r >= 0 && r < m && c >= 0 && c < n && dist[r][c] == -1)
{
q.push({r, c});
dist[r][c] = dist[row][col] + 1;
ans = max(ans, dist[r][c]);
}
}
}
return ans;
}
};