跳石板

分析后可知

要在众多解中寻找最优解

因此用动态规划

比如：

4-6只需跳一步，而6-8也只需一步，因此在刚才跳了一步的基础上再加1

8到10一步，8到12一步，9到12一步，8-10-12两步，因此到12位置时，记下最小需要到达的步数和一步，那么累加就是需要三步到达12

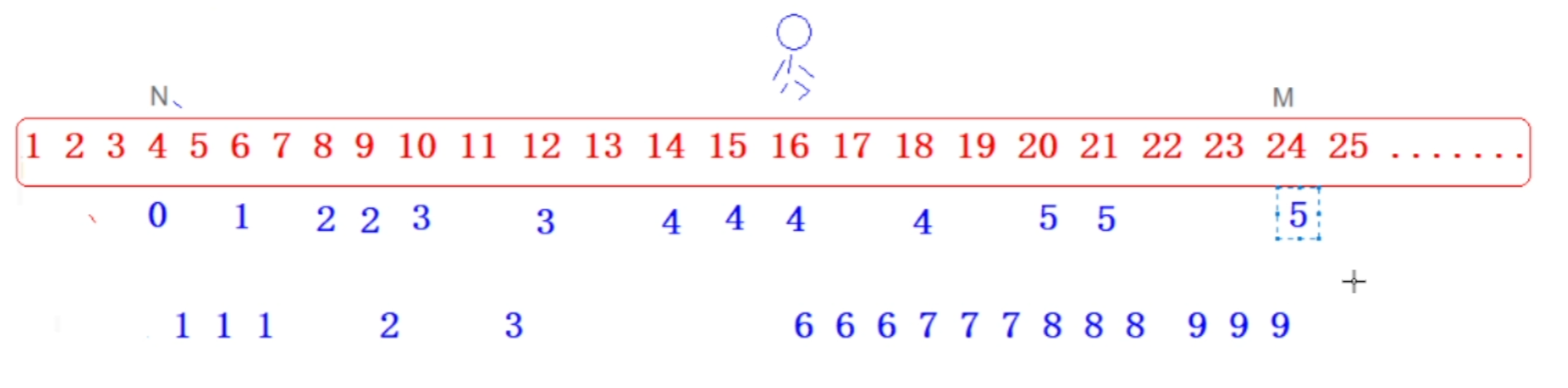
完整过程

#define _CRT_SECURE_NO_WARNINGS 1
#include <limits.h>
#include <iostream>
#include <algorithm>
#include <vector>
#include <math.h>
using namespace std;
void get_divnum(int num, vector<int>& v) {
    for (int i = 2;i <= sqrt(num);++i)
    {
        if (num % i == 0)
        {
            v.push_back(i);
            if (num / i != i)
            {
                v.push_back(num / i);
            }
        }
    }
}
int jumpStone(int n, int m) {
    //设定跳到此区间内的石板时所需要的步数
    //默认为不可到达，设置为整型最大值
    vector<int> step(m + 1, INT_MAX);
    step[n] = 0;
    for (int i = n; i < m; ++i)
    {
        if (step[i] == INT_MAX) {
            continue;
        }

        vector<int> div_num;//存约数
        get_divnum(i, div_num);

        for (int j = 0; j < div_num.size(); ++j)
        {
            if (i + div_num[j] <= m && step[i + div_num[j]] != INT_MAX)
            {
                step[i + div_num[j]] = step[i + div_num[j]] < step[i] + 1 ? step[i + div_num[j]] : step[i] + 1;
            }
            else if (i + div_num[j] <= m)
            {
                step[i + div_num[j]] = step[i] + 1;
            }
        }
    }
    return step[m] == INT_MAX ? -1 : step[m];
}
int main() {
    int n, m, min_step;
    while (cin >> n >> m) { // 注意 while 处理多个 case
        min_step = jumpStone(n, m);
        cout << min_step;
    }
    return 0;
}
// 64 位输出请用 printf("%lld")

    cout << min_step;
}
return 0;

}
// 64 位输出请用 printf(“%lld”)