目录
1 基础知识
1.1 队列 queue
1.2 栈 stack
1.3 常用数据结构
1.4 排序
2 98. 验证二叉搜索树
3 230. 二叉搜索树中第 K 小的元素
4 199. 二叉树的右视图
菜鸟做题忘了第几周,躺平过了个年TT
1 基础知识
1.1 队列 queue
- queue<type> q:定义一个参数类型为 type 的队列
- q.push(variable):在队尾插入一个元素
- q.pop():删除队列第一个元素
- q.size():返回队列中元素个数
- q.empty():如果队列空则返回 true
- q.front():返回队列中的第一个元素
- q.back():返回队列中最后一个元素
1.2 栈 stack
- stack<type> s:定义一个参数类型为 type 的栈
- s.push(variable):压栈,无返回值
- s.emplace():压栈,无返回值(参见原文)
- s.pop():栈顶元素出栈,不返回元素,无返回值
- s.top():返回栈顶元素,该元素不出栈
- s.empty():判断栈是否为空,是返回 true
- s.size():返回栈中元素数量
参考博客:C++ 栈(stack)使用简述
1.3 常用数据结构
- vector<type> v + push_back
- unordered_set<type> s + insert
- unordered_map<type, type> m
1.4 排序
总是忘记如何调用 sort()。。。
假设 vals 是一个容器。sort() 没有返回值,vals 里面就已经是排好的顺序了。
sort(vals.begin(), vals.end())2 98. 验证二叉搜索树
题眼:
- 节点左子树中的所有节点 都 比当前节点小
- 节点右子树中的所有节点 都 比当前节点大
解题思路:
针对位于左子树的节点,判断它是否大于 leftMax;针对位于右子树的节点,判断它是否小于 rightMin;违反任一原则,都不是有效二叉搜索树。
思路说明图:

当前节点(蓝色)作为分界线,一是作为其左子树(绿色)所有节点的上限,二是作为其右子树(黄色)所有节点的下限。当处理到 “6” 这节点时,它同样地,一是作为其左子树(“3”)所有节点的上限,二是作为其右子树(“8”)所有节点的下限。
对于节点 “3”,它的下限是 “5”,上限是 “6”;对于节点 “8”,它的下限是 “6”,没有上限。
class Solution {
public:
bool helper(TreeNode* root, long long leftMax, long long rightMin) {
if (!root) return true;
if (root->val >= leftMax || root->val <= rightMin) return false;
return helper(root->left, root->val, rightMin)
&& helper(root->right, leftMax, root->val);
}
bool isValidBST(TreeNode* root) {
return helper(root, LONG_MAX, LONG_MIN);
}
};说明:什么是 LONG_MAX、LONG_MIN?
c++ 中最大值最小值的设定
3 230. 二叉搜索树中第 K 小的元素
解题思路:
- 遍历二叉树,将所有节点的数值存入一个数组中
- 使用 sort 对数组进行排序
- 返回 K - 1 号元素
class Solution {
public:
vector<int> vals;
void helper(TreeNode * root) {
if (!root) return;
vals.push_back(root->val);
helper(root->left);
helper(root->right);
}
int kthSmallest(TreeNode* root, int k) {
helper(root);
sort(vals.begin(), vals.end());
return vals[k - 1];
}
};4 199. 二叉树的右视图
直接参照 102. 二叉树的层序遍历
解题思路:
- 按 “层” 来遍历二叉树
- 从右向左将同一层的节点的左右子节点插入到队列中
- 在下一 “层” 循环中,队列将从右到左弹出下一 “层” 的所有节点
- 将下一 “层” 的最右侧节点的值插入到数组中
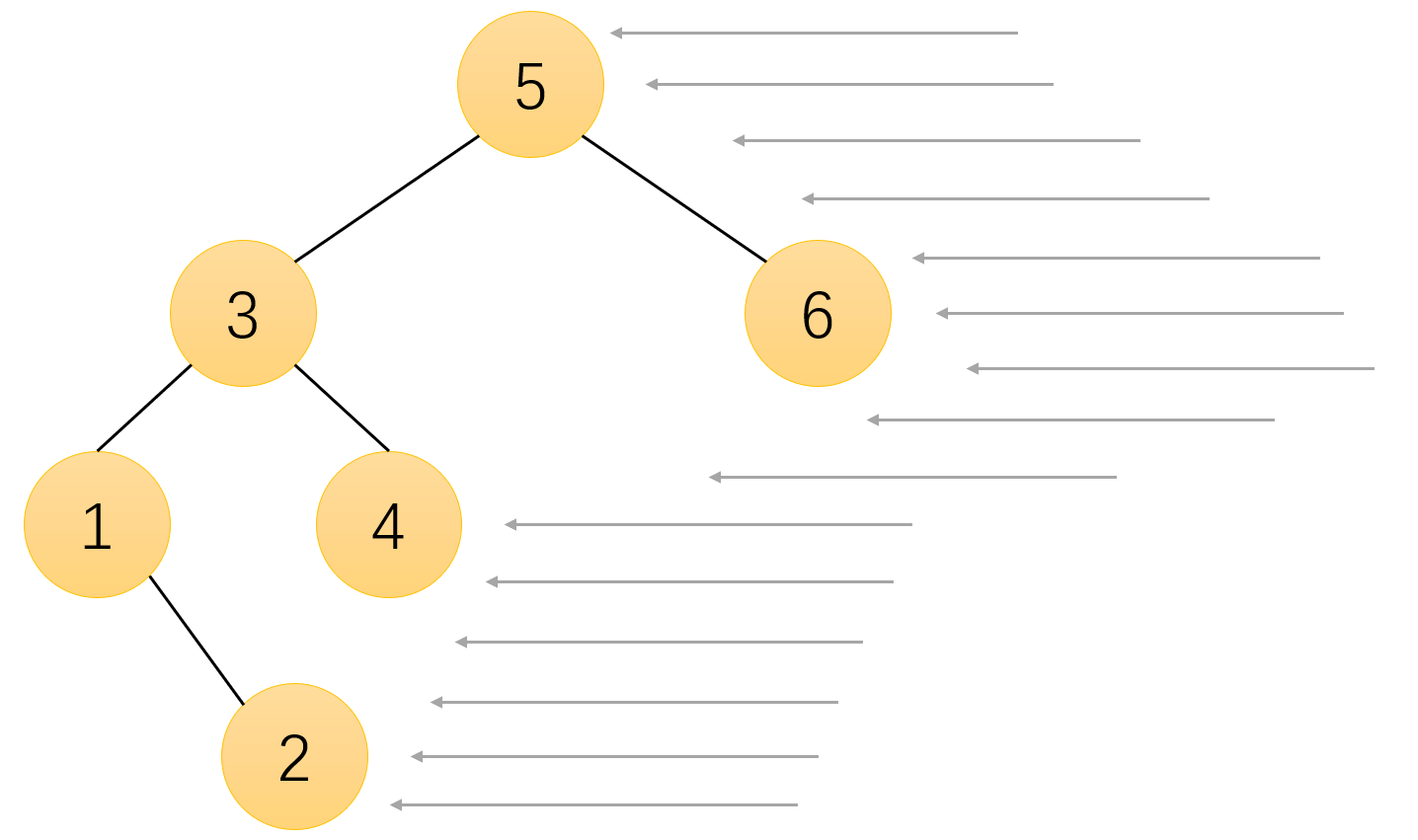
思路说明:
首先将 “5” 插入到队列中。在 “5” 所处的 “层” 的循环中,弹出 “5”,依次将 “5” 的右子节点 “6” 和左子节点 “3” 插入到队列中。由于 “5” 是第一个弹出的节点,因此还要将其值插入到数组中。循环结束。接下来,在 “6” 所处的 “层” 的循环中,弹出 “6”,依次将 “6” 的右子节点和左子节点插入到队列中。由于 “6” 是第一个弹出的节点,因此还要将其值插入到数组中。再弹出 “3”,以此类推,……,直到循环结束。
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
if (!root) return {};
vector<int> vals;
queue<TreeNode *> q;
q.push(root);
while (!q.empty()) {
int currentLevelSize = q.size();
for (int i = 0; i < currentLevelSize; ++i) {
TreeNode * node = q.front();
q.pop();
if (i == 0) vals.push_back(node->val);
if (node->right) q.push(node->right);
if (node->left) q.push(node->left);
}
}
return vals;
}
};说明:以下代码用于判断当前节点是否是最右侧节点
if (i == 0)