话不多说,直接看题:

首先我们考虑暴力,用二维前缀和即可,复杂度为o(n^4).
其实,我们不妨枚举任意2行,枚举以这个为边界的最大矩阵。
我们把其中的每一列前缀和维护出来,相当于把一个矩阵压缩成了一个序列,然后问题就转化为了求一个序列的最大子段和。
下面为AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,a[300][300],lie[300][300],b[300],hh[300];
int ck(){
int ss=-0x3f3f3f3f;
memset(hh,0,sizeof(hh));
for(int i=1;i<=n;i++){
hh[i]=max(b[i],b[i]+hh[i-1]);
ss=max(ss,hh[i]);
}
return ss;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>a[i][j];
lie[i][j]=a[i][j]+lie[i-1][j];
}
}
int ans=-0x3f3f3f3f;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
for(int k=1;k<=n;k++){
b[k]=lie[j][k]-lie[i][k];
}
ans=max(ans,ck());
}
}
cout<<ans;
}扩展一下,假如是求立方体呢?
我们枚举两个x方向与y方向的线,然后在z轴上前缀和压缩即可,复杂度为o(n^5)
接题:
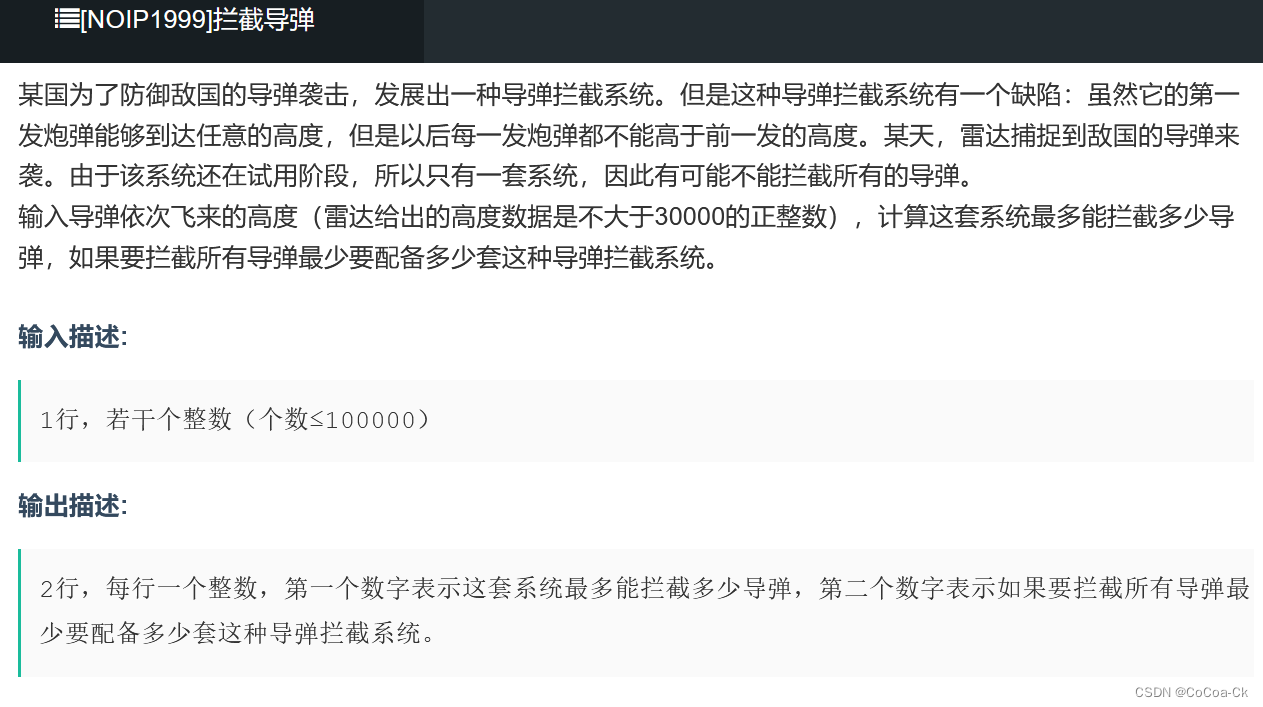
第一问就是求导弹的最长不上升子序列。
对于第二问当高度递增时,要打全部需要相应的个数,换句话说就是至少要导弹的最长上升子序列。
其实,这个数量刚刚可以,我们不妨用反证法,假如还需要一个,不妨假设它栏A与B(A<B)高度间的一个C,假如他比B高,那么我栏B的导弹栏C即可,假如比A高并比B低,矛盾,假如比A低则不需要。因此,数量刚刚可以。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int b,cnt,a[100010],dp1[100010],dp2[100010];
int main(){
while(cin>>b){
a[++cnt]=b;
}
for(int i=1;i<=cnt;i++){
dp1[i]=1;
for(int j=1;j<i;j++){
if(a[j]>=a[i]){
dp1[i]=max(dp1[i],1+dp1[j]);
}
}
}
int ans=1;
for(int i=1;i<=cnt;i++){
ans=max(ans,dp1[i]);
}
cout<<ans<<endl;
for(int i=1;i<=cnt;i++){
dp2[i]=1;
for(int j=1;j<i;j++){
if(a[j]<a[i]){
dp2[i]=max(dp2[i],1+dp2[j]);
}
}
}
ans=1;
for(int i=1;i<=cnt;i++){
ans=max(ans,dp2[i]);
}
cout<<ans;
}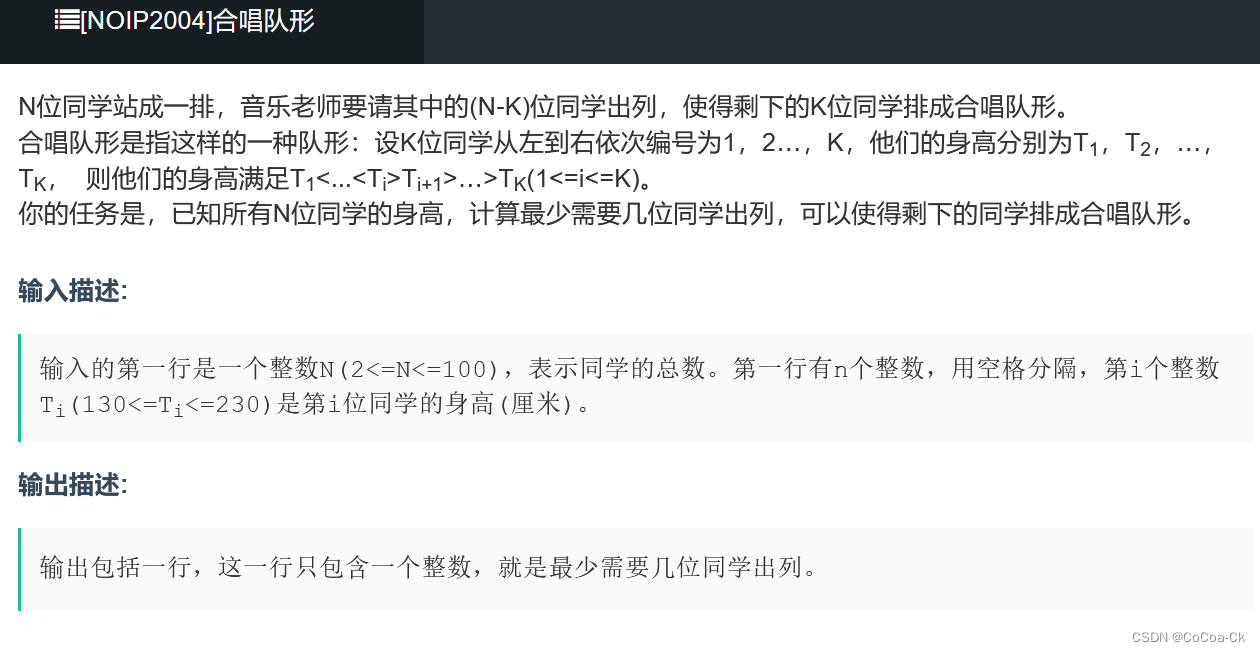
我们不妨设f[i][0]表示上升的最大长度(i必选),f[i][1]表示先上升在下降的最大长度(i必选)
于是我们得到转移方程f[i][0]=max(1+f[k][0]),f[i][1]=max(f[k][0]+1,f[k][1]+1)
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int b,cnt,a[100010],dp1[100010],dp2[100010];
int main(){
while(cin>>b){
a[++cnt]=b;
}
for(int i=1;i<=cnt;i++){
dp1[i]=1;
for(int j=1;j<i;j++){
if(a[j]>=a[i]){
dp1[i]=max(dp1[i],1+dp1[j]);
}
}
}
int ans=1;
for(int i=1;i<=cnt;i++){
ans=max(ans,dp1[i]);
}
cout<<ans<<endl;
for(int i=1;i<=cnt;i++){
dp2[i]=1;
for(int j=1;j<i;j++){
if(a[j]<a[i]){
dp2[i]=max(dp2[i],1+dp2[j]);
}
}
}
ans=1;
for(int i=1;i<=cnt;i++){
ans=max(ans,dp2[i]);
}
cout<<ans;
}接题:

我们换一次需要用一次次数得到下-上的值,容易与想到与背包问题类似。
于是我们类比定义:f[i][j]为前i个骨牌得到j的最小次数。
易得转移方程:f[i][j]=min(f[i-1][j-(上-下)],f[i-1][j+(上-下)]+1)
有俩个细节:1.对于初值我们赋值为正无穷。
2.对于负数问题,我们平移处理。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define ck 5001
int n,dp[2][10010];
struct node{
int shang,xia;
}a[1010];
int main(){
cin>>n;
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].shang,&a[i].xia);
memset(dp,0x3f,sizeof(dp));
dp[0][0+ck]=0;
for(int i=1;i<=n;i++){
for(int j=-5*i+ck;j<=5*i+ck;j++){
int hh=a[i].shang-a[i].xia;
dp[i%2][j]=min(dp[(i-1)%2][j-hh],dp[(i-1)%2][j+hh]+1);
}
}
int mm=ck;
if(dp[n%2][ck]<=n) cout<<dp[n%2][ck];
else{
int i=ck-1,j=ck+1;
for(;i>=0;i--){
if(dp[n%2][i]<=n) break;
}
for(;j<=10009;j++){
if(dp[n%2][j]<=n) break;
}
if(i+j==2*ck) cout<<min(dp[n%2][i],dp[n%2][j]);
else if(i+j>2*ck) cout<<dp[n%2][i];
else cout<<dp[n%2][j];
}
}