参考资料:用python动手学统计学
1、导入库
# 导入库
# 用于数值计算的库
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
# 用于绘图的库
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# 用于估计统计模型的库
import statsmodels.formula.api as smf
import statsmodels.api as sm2、数据准备
data=pd.DataFrame({
'beer':np.array([45.3, 59.3, 40.4, 38. , 37. , 40.9, 60.2, 63.3, 51.1, 44.9, 47. ,
53.2, 43.5, 53.2, 37.4, 59.9, 41.5, 75.1, 55.6, 57.2, 46.5, 35.8,
51.9, 38.2, 66. , 55.3, 55.3, 43.3, 70.5, 38.8]),
'temp':np.array([20.5, 25. , 10. , 26.9, 15.8, 4.2, 13.5, 26. , 23.3, 8.5, 26.2,
19.1, 24.3, 23.3, 8.4, 23.5, 13.9, 35.5, 27.2, 20.5, 10.2, 20.5,
21.6, 7.9, 42.2, 23.9, 36.9, 8.9, 36.4, 6.4])
})
data.head()3、绘图,初识数据基本情况
sns.jointplot(x='temp',y='beer',data=data)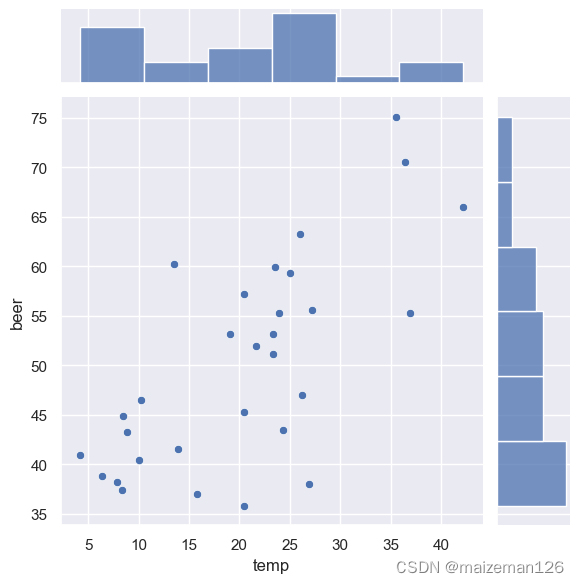
由散点图可以看出啤酒(beer)的销量与温度(temp)有正相关的关系。
4、建立正态线性模型
# 利用最小二乘法(ordinary least squares)拟合线性模型
lm=smf.ols(formula="beer ~ temp",data=data).fit()
# 输出拟合结果
lm.summary()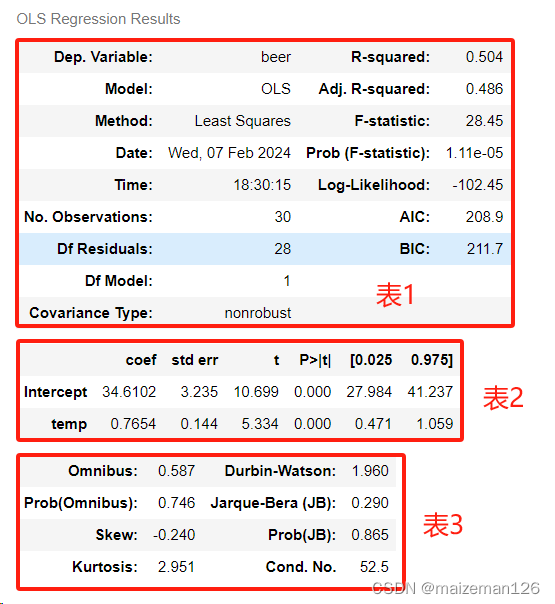
表1中有关指标的含义如下:
Dep.Variable:响应变量的名称,Dep为Depended的缩写。
Model/Method:这里显示为OLS,即普通最小二乘法。
Date/Time:对模型进行估计的日期和时间。
No.Observations:样本容量。
Df Residuals:残差自由度,样本容量减去参与估计的参数个数。
Df Model:模型自由度,参数个数-1。
Covariance Type:协方差类型,默认为nonrobust
R-squared:决定系数。
Adj.R-squared:矫正决定系数。
F-statistic:为方差分析的F统计量。
Prob(F-statistc):F统计量对应的概率值。
Log-Likehood:最大对数似然。
AIC:赤池信息量准测。
BIC:贝叶斯信息量准测。
表2为回归系数的t检验分析结果,可见intercept(截距)和temp(temp列的回归系数)均达到极显著水平,且temp回归系数大于0。说明气温会影响啤酒销售额,且气温越高啤酒销售额也越高。
可以用lm.params属性单独将截距和回归系数导出。
# 获取线性模型的参数
lm.params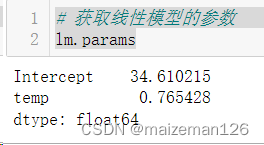







![[计算机网络]---Https协议](https://img-blog.csdnimg.cn/direct/85bf14fbb03f4966aefc4b1e362001cc.png)