🌈 博客个人主页:Chris在Coding
🎥 本文所属专栏:[深度学习]
❤️ 热门学习专栏:[Linux学习]
⏰ 我们仍在旅途

目录
1.卷积的定义
2.卷积的"卷"在哪里
3.什么又是卷积神经网络
4.卷积神经网络的第一层的作用及其与卷积的关系
5.卷积的三层含义
1.卷积的定义
卷积(Convolution)是数学和计算机科学中一种重要的操作,常用于信号处理、图像处理、神经网络等领域。在信号处理和图像处理中,卷积用于将两个信号或图像进行融合,生成一个新的输出信号或图像。在神经网络中,卷积层是一种常见的层类型,用于从输入数据中提取特征。
- 在离散情况下,卷积的定义为:
- 在连续情况下,卷积的定义为:
2.卷积的"卷"在哪里
卷积的名字来源于它的运算过程。在卷积操作中,我们将两个函数进行加权求和,并在不同的位置进行移位。这个过程可以类比为将一个函数“卷”到另一个函数上,并对其进行加权叠加。这种“卷”的过程使得卷积得名。
当然就这样说过于抽象抽象,我们不妨直接直接举个例子来感受:

咱就说那吃饭来说,分别描述了一个人的进食和消化过程。这个过程可以用两个函数来表示:
- f(t)函数描述了他待消化食物剩余情况
- g(t)函数描述了他的消化情况
- 我们假设一个人的消化过程是固定的函数,即g(t),食物剩余的百分比随时间的流逝都保持相同的变化
- 而相对应的待消化食物剩余量的函数f(t)则显得随机,不固定,这时由于我们会有随机的进食行为
这个时候,我们在已知在8点的时候我们吃了面条,10点时我们吃了面包,而12点时我们又进食了米饭
这个时候如果我们想要去求14点时肠胃中的剩余食物,即f(14)时,我们可以得到下面这个公式
此时胃里在下午14点剩下的东西则为米饭剩余量+面包剩余量+面条剩余量。也就是图片右边的三个公式之和
既然这样,我们可不可以推广一下这个计算方法?
如果现在要求的是任意t时刻胃里还剩多少东西
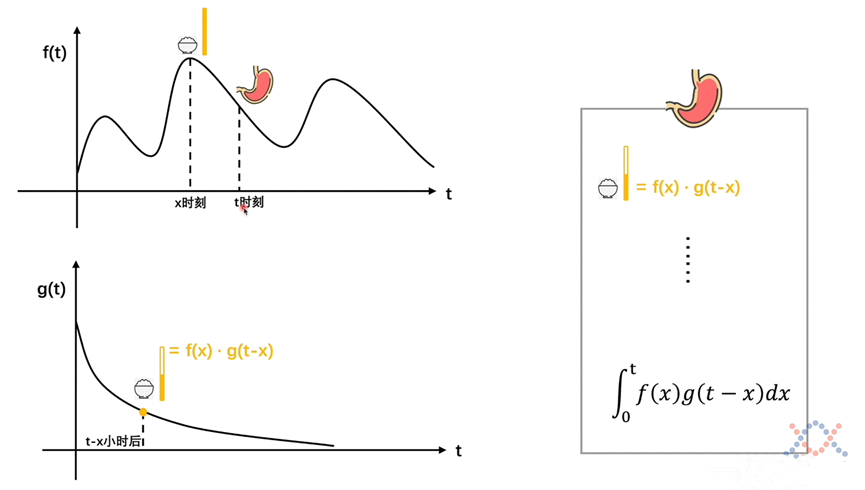
那其实就是要把把在t时刻之前,对应的每一个时间吃的食物的剩余量分别算出来,在进行相加。
这是不是就和我们前面的离散型卷积公式一模一样
也就是说,通过卷积操作,我们可以得到在某一时刻他胃里还剩下多少食物,这个过程就好像是将消化情况“卷”到进食情况上,然后根据位置和时间进行加权叠加,最终得到一个关于时间的函数,表示在每个时刻他的胃里还剩下多少食物。
在图像上体会x和t-x在图像上的对应关系
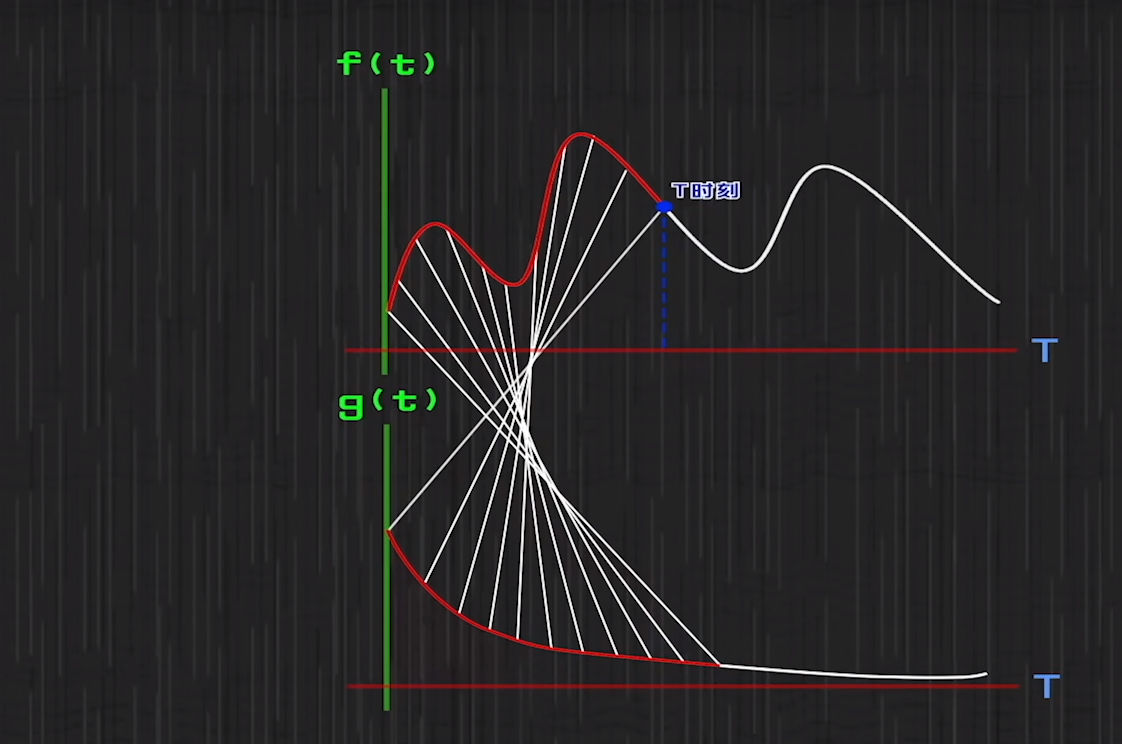 这时候我们我们把两个函数每个时刻对应相乘的点连接起来,会发现看起来十分别扭难受
这时候我们我们把两个函数每个时刻对应相乘的点连接起来,会发现看起来十分别扭难受
如果这个时候我们把记函数翻转一下,会怎么样呢

是不是豁然开朗了,所以说啊卷积说得通俗一点,就是把记函数翻转一下,因为翻转了所以叫卷积
在这个问题的基础上我们甚至可以总结一下卷积的含义:
一个系统满足:
- 输入不稳定,对应f(t)
- 输出稳定,对应g(t)
那么我们就可以用卷积求系统的存量
3.什么又是卷积神经网络
卷积神经网络(Convolutional Neural Network,CNN)是一种深度学习模型,专门用于处理具有网格结构数据的任务,例如图像识别、语音识别和自然语言处理等。
就卷积神经网络识别图片而言,它之所以叫卷基神经网络就是因为在把图片交给神经网络之前,先要对图像进行一个卷积操作。
我们前面才总结了卷积的定义,也就是要找到那两个函数,一个输入不稳定和一个输出稳定
那就看看什么是卷积操作
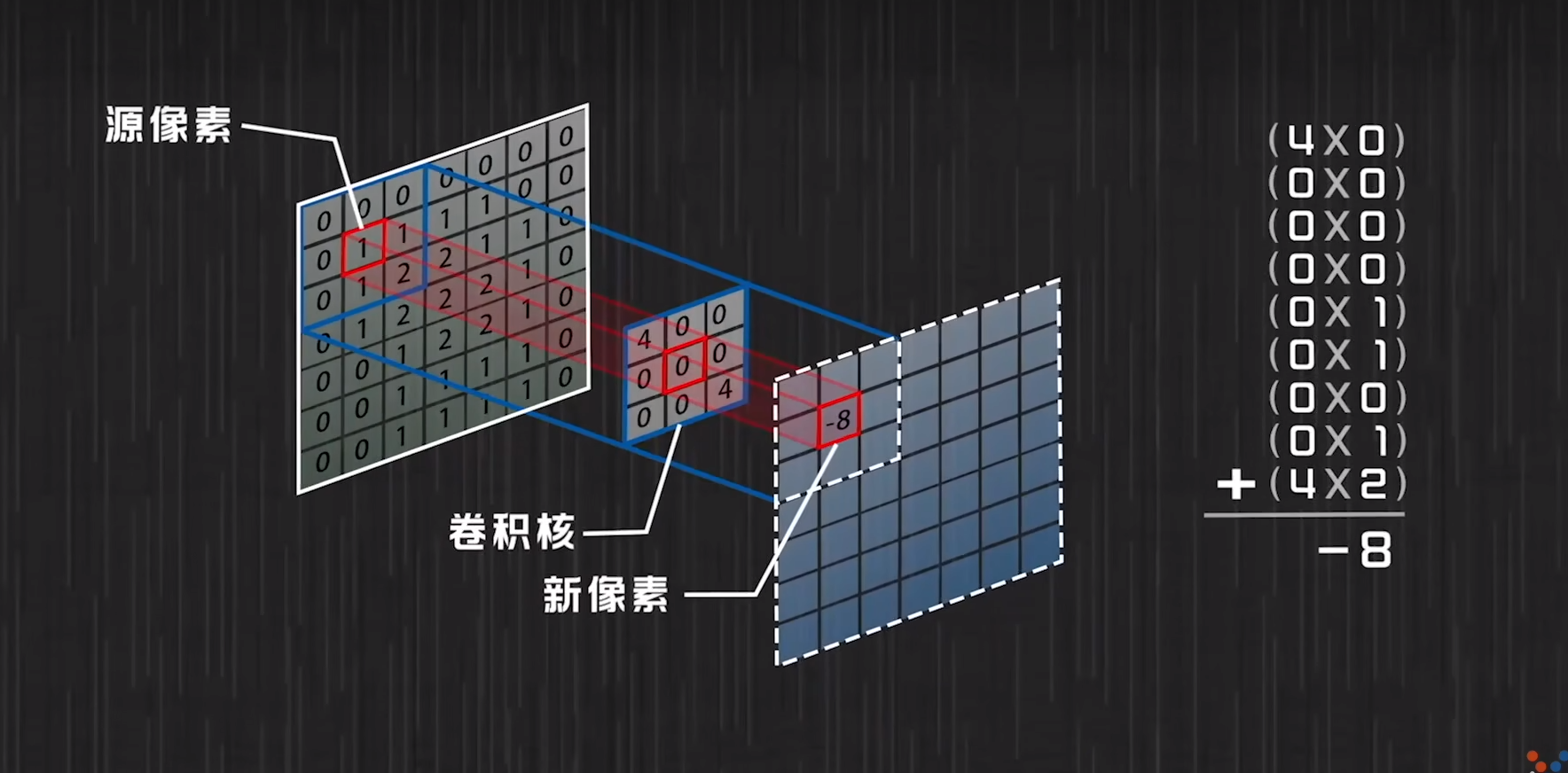

具体来说,卷积操作的步骤如下:
-
卷积核与图像相乘: 将一个小的卷积核(通常是一个小的矩阵)应用于输入图像的局部区域,对应位置的像素值相乘。这相当于将卷积核覆盖在图像的局部区域上,并将卷积核中的值与图像中对应位置的像素值相乘。
-
相乘结果求和: 对相乘得到的结果进行求和,得到新的像素值。这个新的像素值表示了卷积核与图像局部区域之间的相似度或相关性。
-
扫描整个图像: 将卷积核在整个输入图像上移动,重复进行相乘和求和操作。这样就可以得到输出图像中的所有像素值。
-
处理边缘像素: 对于输出图像中的边缘像素,由于卷积核无法完全覆盖,因此可能无法进行完整的卷积操作。一种常见的处理方法是在进行卷积操作之前,对输入图像的边缘进行填充(通常使用零值填充),以确保输出图像与输入图像具有相同的大小。
这时候来看卷积操作,会发现我们之前所学习的f函数和g函数无法进行很好地理解和对应。
这个时候我们得换个视角重新深入理解卷积操作
回到一维问题,这里我们重新来理解一下卷积是什么.假如在t时刻有一个飓风,在x时刻有一只蝴蝶煽动翅膀,在飓风之前有很多蝴蝶对他产生影响,这个影响会随着时间的变化,他的影响力随着时间变化,这个变化就是g函数。
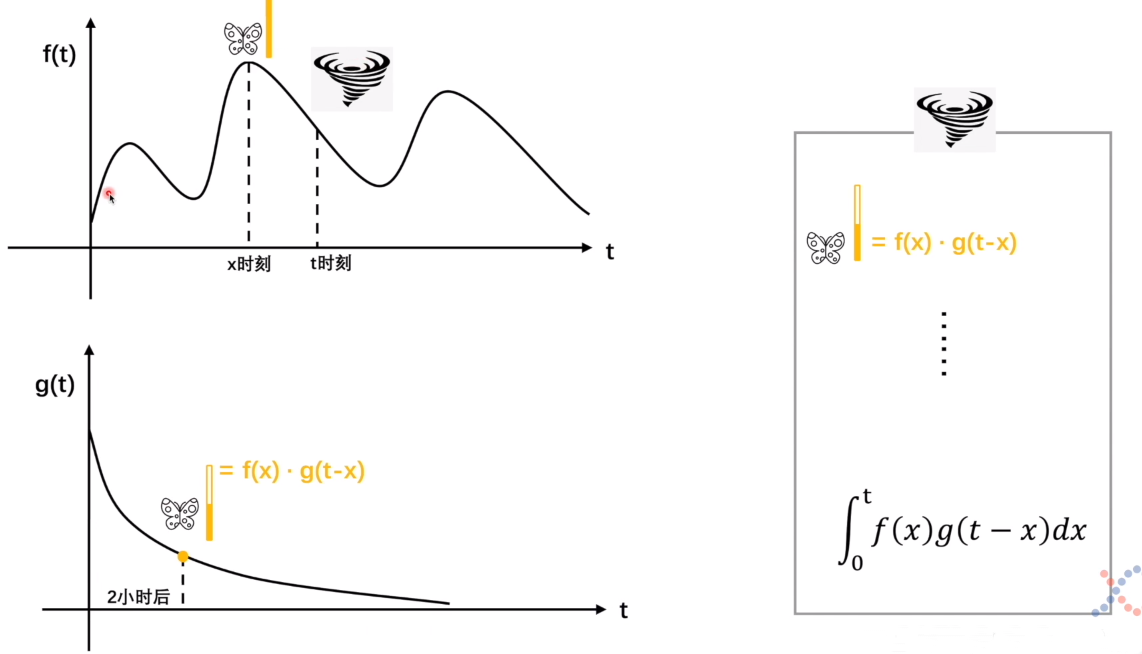
而这个卷积呢,其实就是在处理这个飓风发生的时候,它之前蝴蝶扇动翅膀对自己产生了多少的影响
那如果我们抛开具体的例子,我们是不是就可以这样来去理解卷积
在某一个时刻发生了一件事,而这件事的产生呢它是会受到之前发生很多事的影响的,就比如说在x时刻它发生了一件事,这件事会对t时刻产生影响
具体怎么影响呢?
它还要看从x时刻到t 时刻经历的时间,它会随着时间进行变化而规定
随时间如何变化呢?
就是g(t)函数,g(t)函数就规定了之前发生的一些事情,它随着时间影响力是如何变化的.当然不论是之前吃饭呢还是这个蝴蝶扇动翅膀.从直觉上看它的影响力都是随着时间减小的,但这不是必然的如果我们换一个其他例子.这就有可能随着时间在发生不同的变化甚至还可能是增长
甚至我们还可以把视野放的更广一点
假如说这个影响力的变化不是随着时间产生变化的,而是随着距离,就比如说在t位置发生了一件事
而对这个位置产生影响的是其他的很多位置,就比如说其中一个是x位置,那这样子,这个g(t)函数
它的横坐标也可能变成不是时间而是距离了
我们还是回到图像卷积操作,图像的卷积操作是什么
在图像上进行卷积操作,那会不会它就是在去看很多像素点,对某一个像素点是如何产生影响的呢?
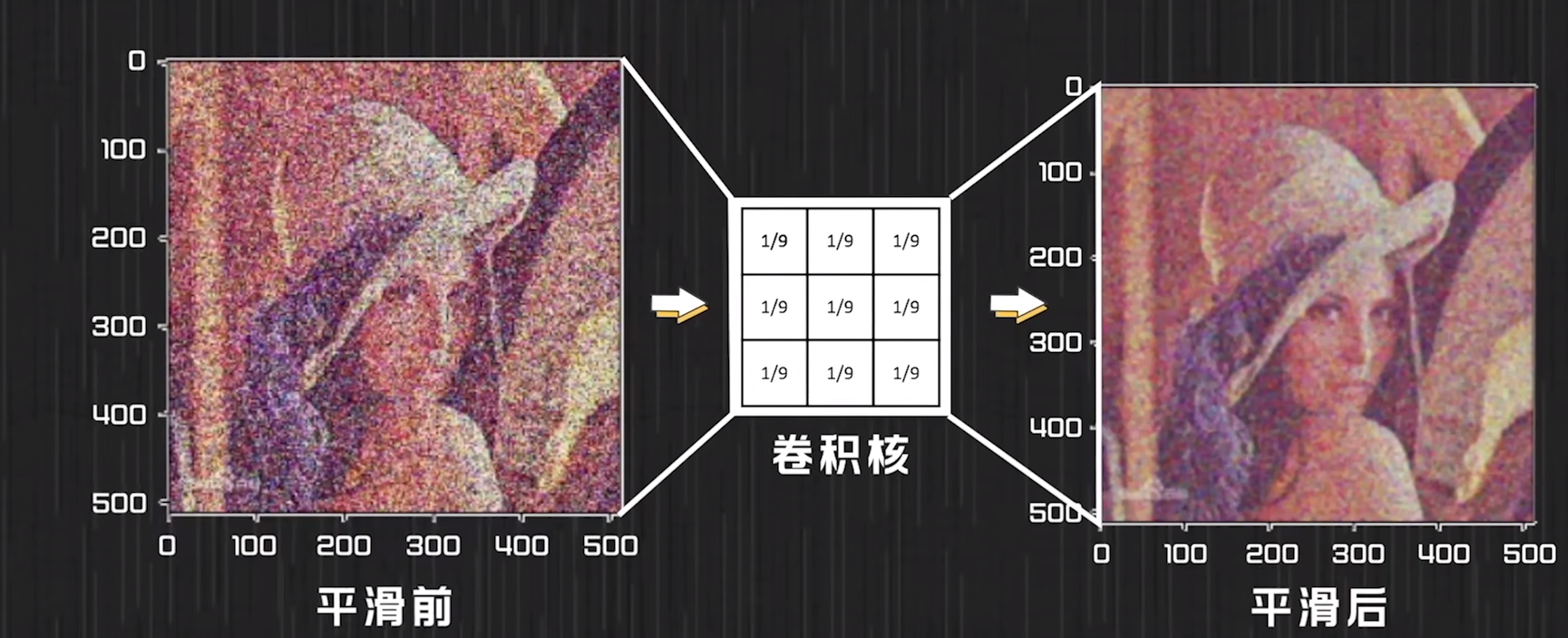
blur操作,即降噪平滑操作.,就是认为目标像素点的值是周围值的平均数,即周围各点对它的影响是一样的,此处卷积核以3X3为例。
什么是平滑操作?
平滑其实就是让周围的像素点和自己相差不要太大,从这个卷积核我们可以看到啊,它是在求平均值,什么是求平均?就是看到周围的像素点和你这个像素点相比啊,这个像素点的数值是不是太高了?如果太高了就拉低点,如果太低了那就拉高一点,如果是这样的话那卷积核就容易理解了它其实就是规定了周围的像素点是如何对当前像素点产生影响的.
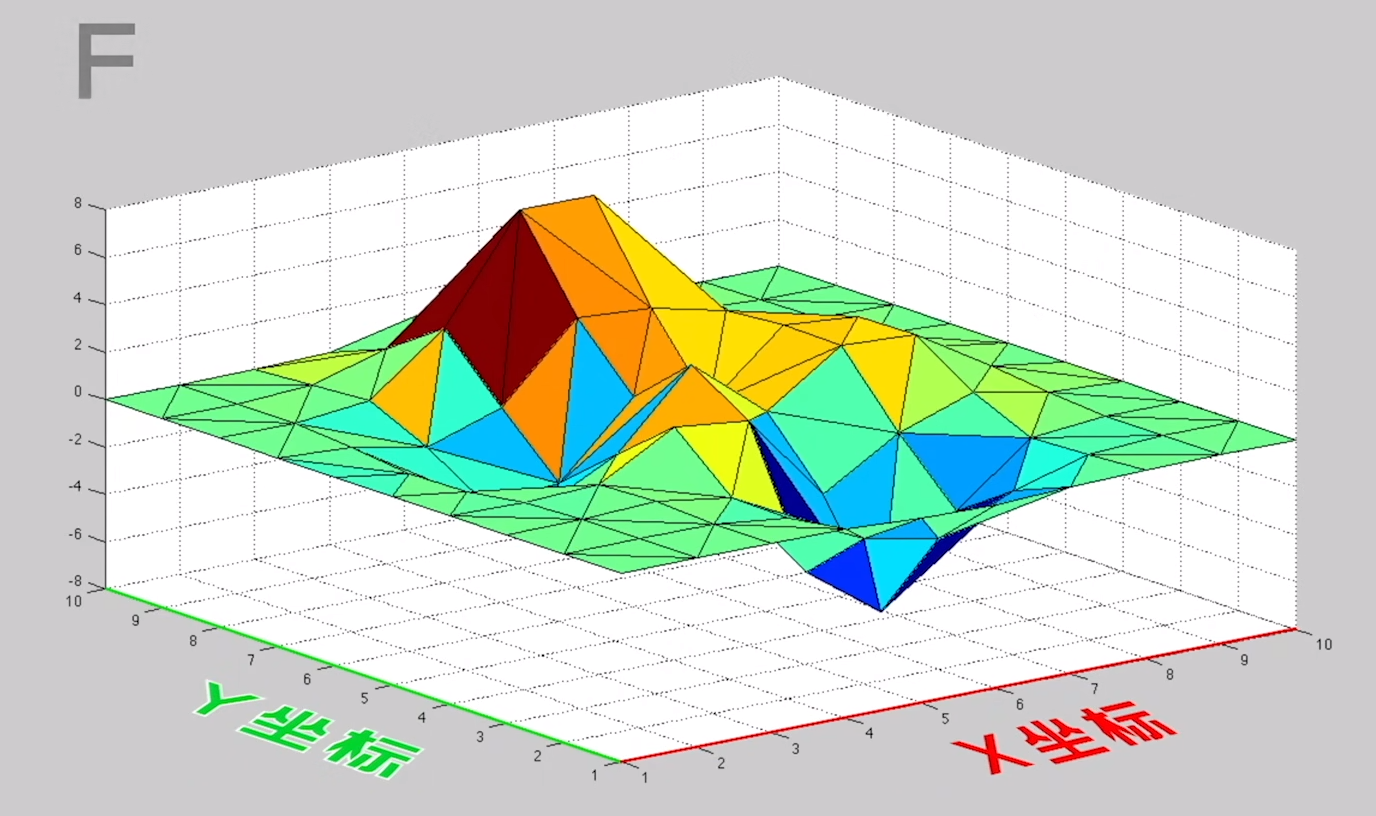

那怎么来从数学上理解二维的卷积操作呢?
现在我们需要考虑(x-1,y-1)的像素点对选定的像素点(x,y)的影响,那我们应该找到他对应的像素值f(x-1,y-1),再乘上其对应的影响比例,即g函数中的值
如图,我们现在假设(x-1,y-1)是x时刻,而(x,y)是t时刻。吃饭的例子是需要用t-x,而此处类比过来则是x-(x-1)以及y-(y-1),那么则对应g(1,1)
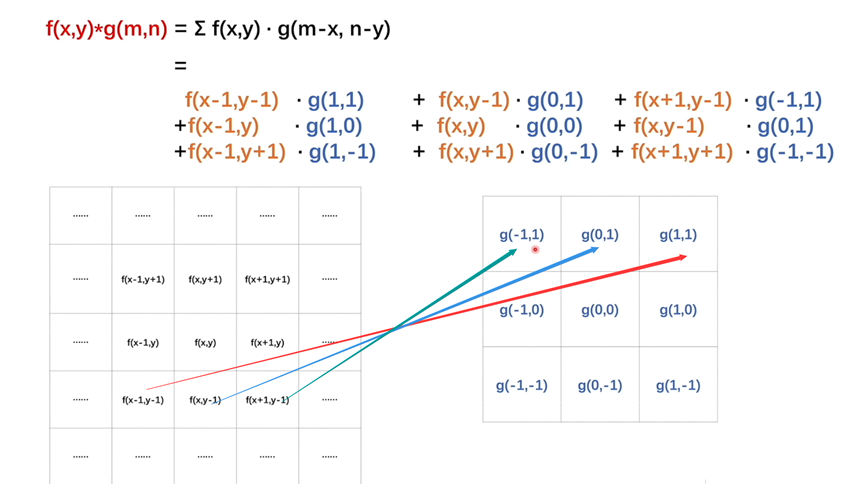
同理,如果把所有的点对应的g函数的情况都计算出来就会如上图所示
其实可以根据箭头的对应关系看出,还是f函数和g函数的一一对应关系还是比较难看的但是此时,我们只需要对g函数的图像旋转180°,就会很清晰了

所以说呢,旋转前表现的是那个g函数,它不等于卷积核.它要旋转180度之后才是卷积核
卷积核它是可以扣在图像上直接相乘再相加,它其实是已经把旋转这个步骤啊给省略了
但是它本质上仍然是一个卷积运算
4.卷积神经网络的第一层的作用及其与卷积的关系
卷积操作,是卷积神经网络第一层的关键,这又有点像是人的视网膜,看到图像之后啊,先进行一个预处理,然后再交给大脑
卷机神经网络,一般是用来做图像识别的,就比如这种情况
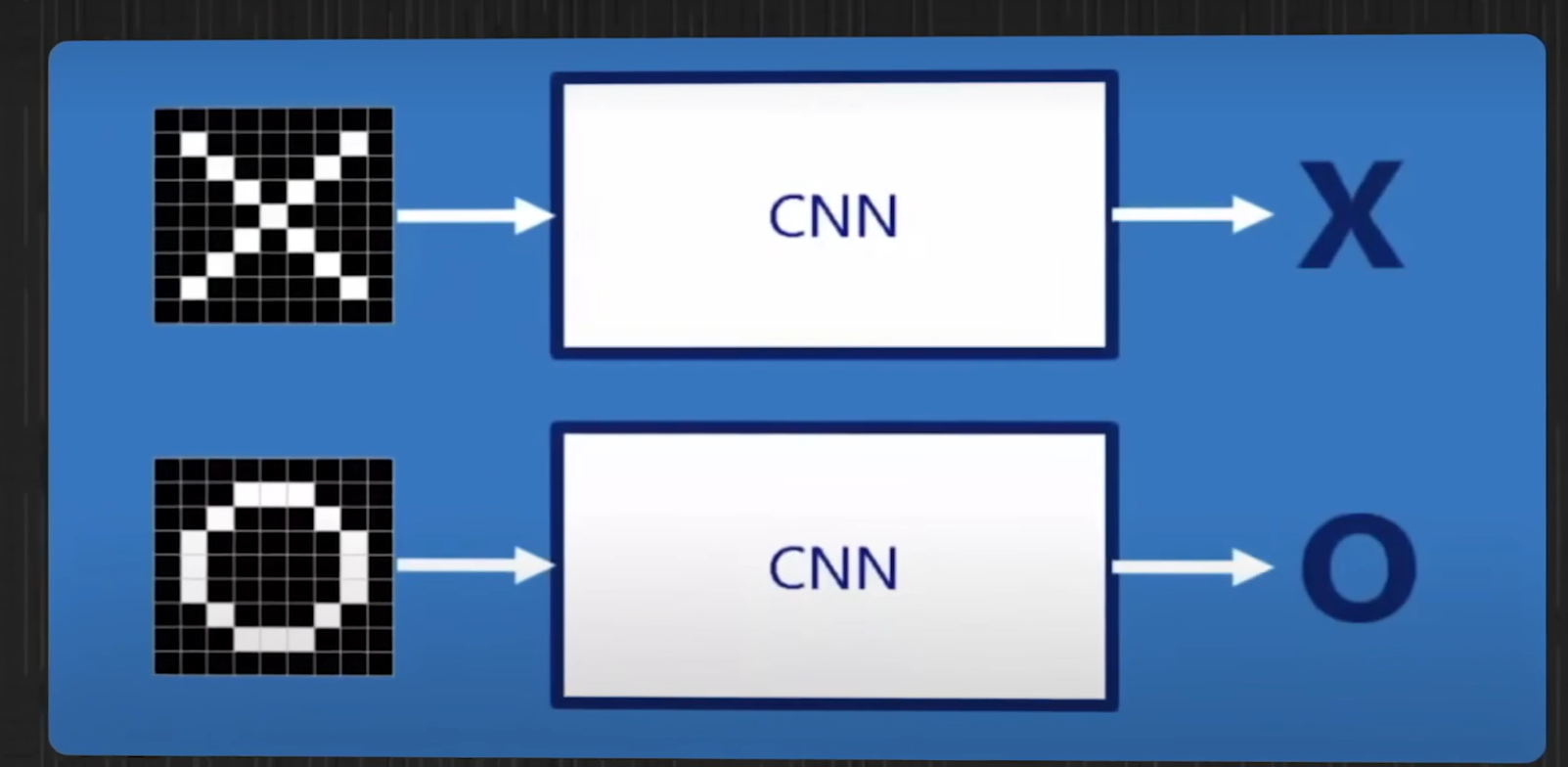
输入图片里面的有差有圆,通过卷积神经网络就能识别出来,它们是x和o,但重点呢,不是识别这种规规整整的情况,而是像下面这样不规整的差和圆

这种情况我们人是能一眼就看出来的,但是交给计算机就不行了,因为计算机看到的都是这样的情况
像素点都是数字,当然了这里是把问题简化了一下认为一个像素就有两种情况1和-1

如果把像素点挨个进行比较的话,这就是两种东西是不一样的
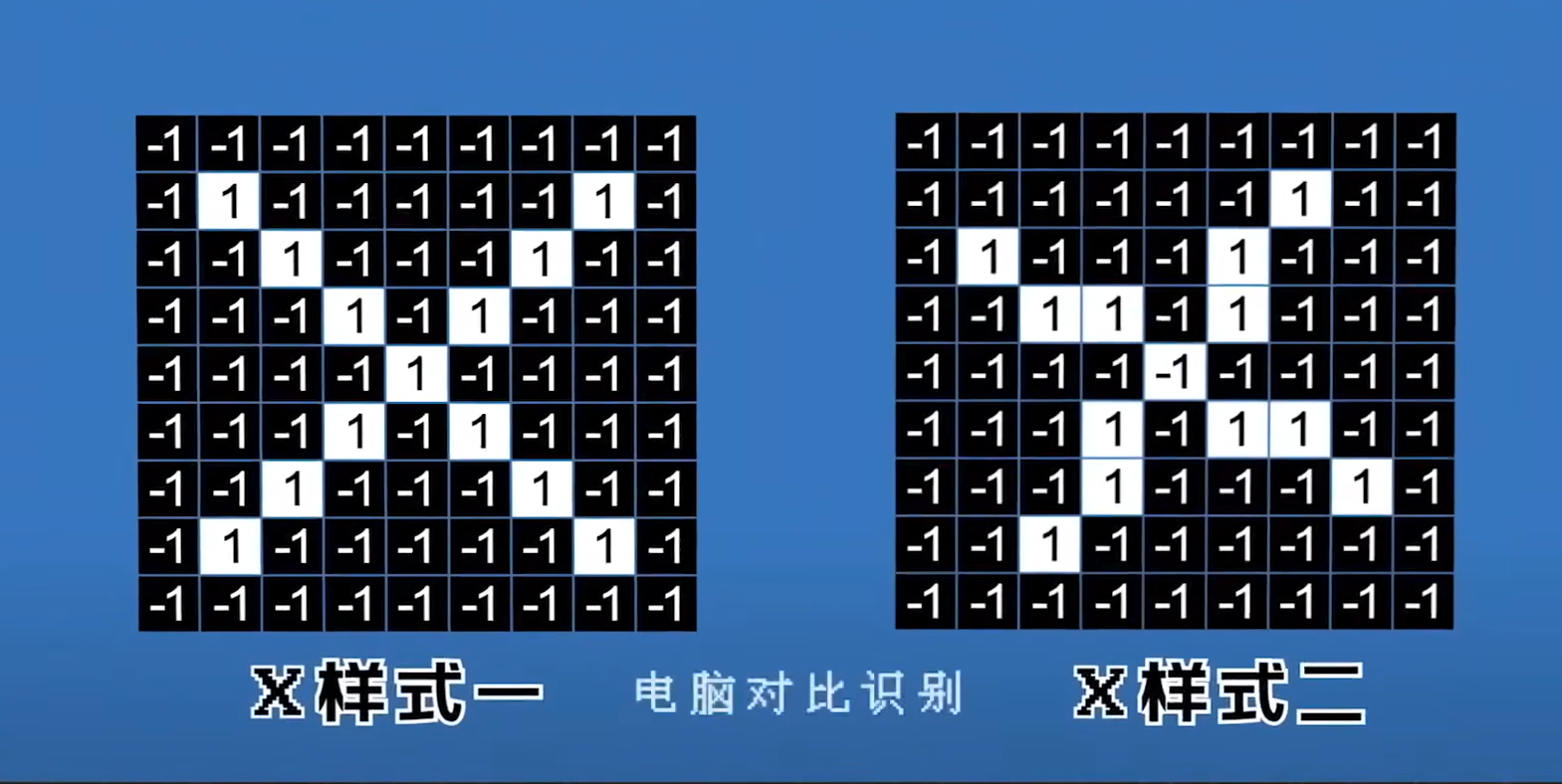
其实我们仔细看的话,可以发现,两边的图像虽然不同,但是如果只看局部的话,还是有相同地方的

所以卷积神经网络识别图像的第一步,就是把图像的局部特征给调出来,把这些局部特征交给神经网络,由神经网络去判断
卷积还怎么还能去提取图像的局部特征呢?
我们之前所说的卷积核只是平滑卷积核,目的是让图像经过卷积操作后变得更加平滑朦胧。
但事实上,卷积操作还有很多的卷积核。
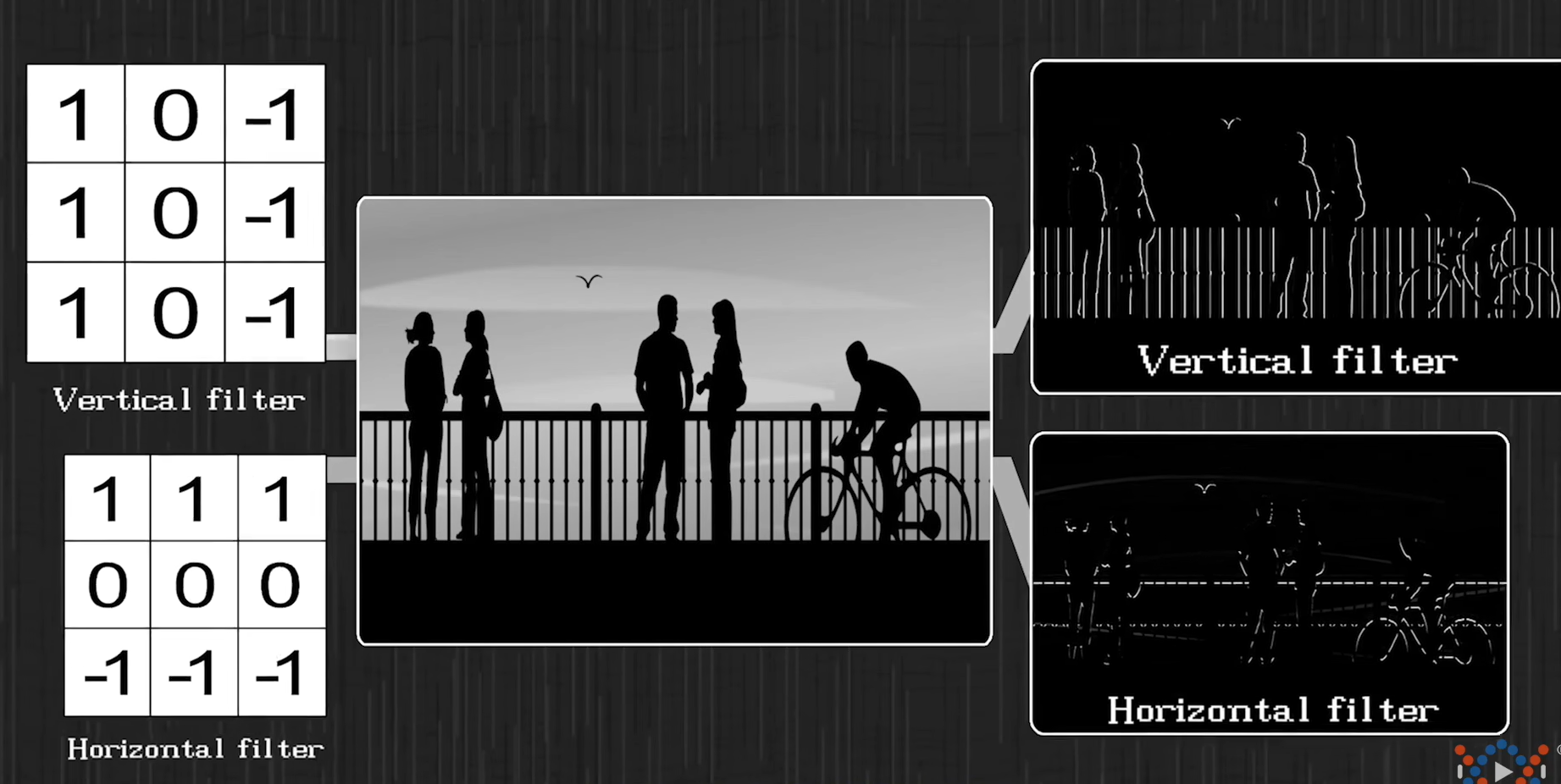
所以,卷积操作其实还有个功能,如果挑选的卷积和合适,最后就可以对图片进行过滤,把某些特征保存下来 而其他的特征就被过滤掉了。此时,卷积核被叫做过滤器,上图所展示的两个卷积核分别叫做垂直边界过滤器和水平边界过滤器。
当进行图像处理中的卷积操作时,可以将其理解为像素点之间的相互影响、试探和选择。卷积核就像是一个模板,它在图像上移动时,与每个像素点进行相乘再相加的操作,试图捕捉图像中的特征信息。在平滑卷积操作中,卷积核试图找到图像中的平滑区域,并通过调整像素点的值来使图像变得更加平滑。
在其他类型的卷积操作中,如边缘检测或特征提取,卷积核可能更注重捕捉图像中的不同特征,例如边缘、纹理或形状等。总的来说,卷积操作通过对周围像素点的主动试探和选择,帮助我们从图像中提取出有用的特征信息。(当我们不想考虑某个位置的时候,就可以把它设置成零而,需要重点考虑某个位置的时候,就可以把这个位置的权重设置的比较高,通过卷积核把周围有用的特征给保留了下来。)

回到前面识别x的那个问题,利用这三个卷积核就可以把三个特征都给找出来,分别是左上到右下,全是1. 还有x的位置都是1,以及从左下到右上都是1。

就比如说这种情况吧,就是完美匹配,计算出来的结果是1

而这种情况呢,就可以看出来了,它虽然也能匹配上,但不能算是完美匹配,最后计算的结果就是0.55

将整个图像,都进行一次这样的卷积操作之后,最后就包含了,与这个特征匹配的全部信息
然后再把三个特征的卷积核,都分别再操作一遍,接下来神经网络就开始干活了,神经网络通过对这些特征信息的判断就可以进行图像识别了
5.卷积的三层含义
- 第一层就是吃饭的例子里面一个系统,它有不稳定的输入,有稳定的输出,则可以通过卷积计算系统的存量
- 第二层就是图像处理,一个卷积核其实就是规定周围像素点对当前像素点会产生怎样的影响。
- 第三层就是一个过滤器的卷积核,规定了一个像素点会如何试探周围的像素点,以此筛选图像的特征。
不论哪一层,卷积在数学上其实是没有差别的,它们的意义都是相同的,但是利用到不同的地方,这意义就发生了改变。
最后一句话总结:卷积就是瞬时行为持续性后果的总和













![[力扣 Hot100]Day29 删除链表的倒数第 N 个结点](https://img-blog.csdnimg.cn/direct/d38a793dc83c45febc9742225aff0d26.png)