LeetCode491.非递减子序列
题目描述:
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
示例 1:
输入:nums = [4,6,7,7] 输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
示例 2:
输入:nums = [4,4,3,2,1] 输出:[[4,4]]
解题思路:
·这题也是求子集,以及去重,可能会有同学会以90.子集II的解题思路进行解题,但是,这两题的思路其实并不一样
·在90.子集II中我们通过排序,以及used数组进行去重,但是这题并不能对数组进行排序,所以不能使用之前的去重逻辑
·所以,我们就需要使用set进行去重
代码如下:
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums,int startIndex){
if(path.size() > 1){
result.push_back(path);
}
unordered_set<int> uset;
for(int i = startIndex;i < nums.size();i++){
if((!path.empty() && nums[i] < path.back()) || uset.find(nums[i]) != uset.end()){
continue;
}
uset.insert(nums[i]);
path.push_back(nums[i]);
backtracking(nums,i+1);
path.pop_back();
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
backtracking(nums,0);
return result;
}
};·时间复杂度:O(n*2^n)
·空间复杂度:O(n)
总结:这题对于之前已经养成了思维定式,或者一直套模板的同学而言,起到了很好的警醒作用。可以拓宽大家的思路
LeetCode46.全排列
题目描述:
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1] 输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1] 输出:[[1]]
解题思路:
·这道题与之前的不同,是一个排列问题,首先排列是有序的,也就是说[1,2]和[2,1]是两个集合,这和之前的子集以及组合问题有所不同
·但是也有与之前的相似之处,需要使用used数组作为标记,标记已经选择的元素,如图:
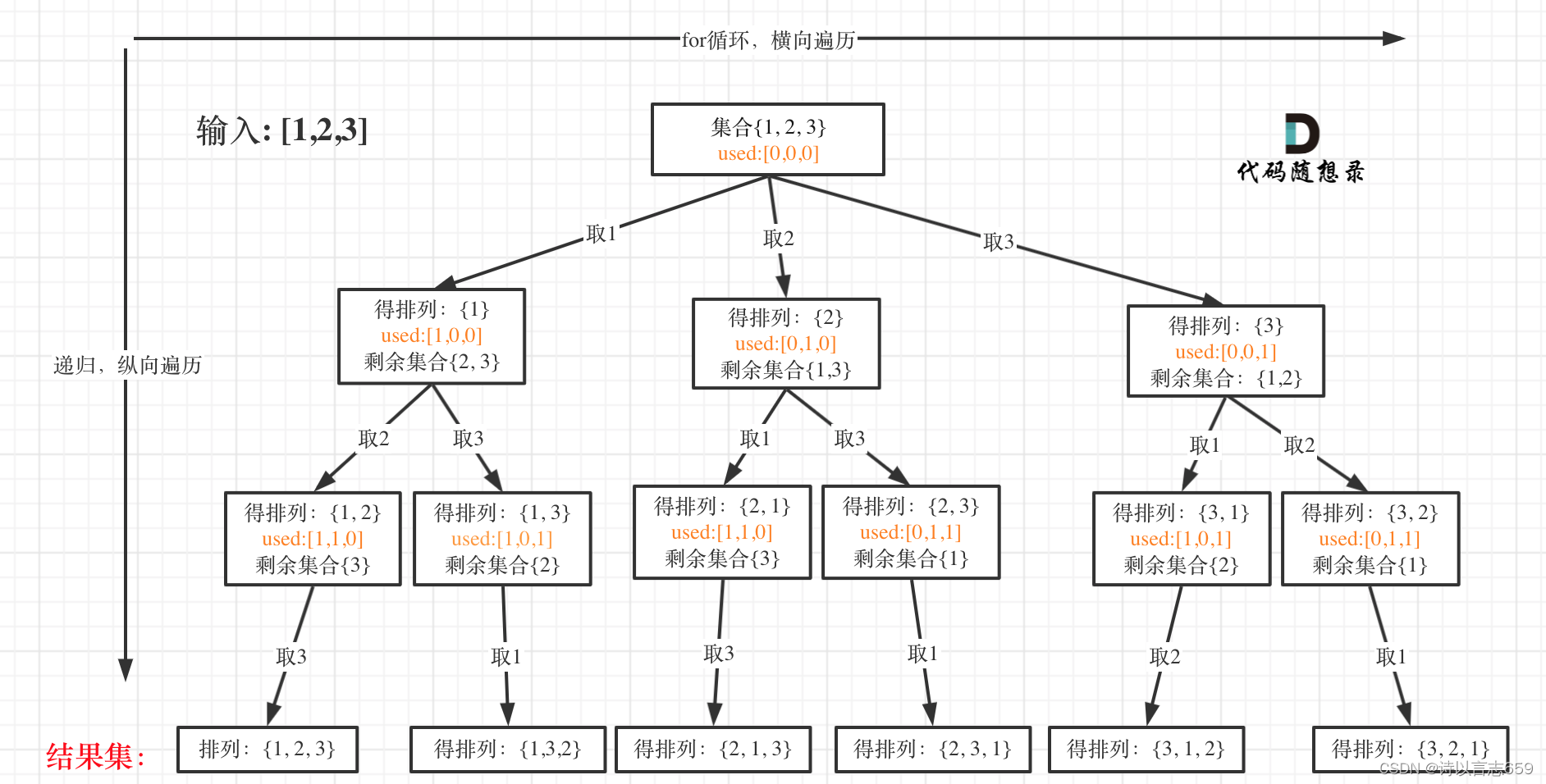
·并且,排列问题因为元素需要被多次使用,所以并不需要使用startIndex
代码如下:
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums,vector<bool>& used){
if(path.size() == nums.size()){
result.push_back(path);
return ;
}
for(int i =0;i < nums.size();i++){
if(used[i] == true) continue;
used[i] = true;
path.push_back(nums[i]);
backtracking(nums,used);
path.pop_back();
used[i] = false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<bool> used(nums.size(),false);
backtracking(nums,used);
return result;
}
};·时间复杂度:O(n!)
·空间复杂度:O(n)
总结:可以直观的看出,排列问题与组合问题的不同点
·每层都从0开始搜索,而不是startIndex
·需要used数组记录path里都放了哪些元素
LeetCode47.全排列II
题目描述:
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2] 输出: [[1,1,2], [1,2,1], [2,1,1]]
示例 2:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
解题思路:
·与上一题的区别在于,给定一个可包含重复数字的序列,要返回所有不重复的全排列,所以只需要对上一题的代码中,增加一个去重代码即可解题
·去重又去排列问题是一样的套路,特别强调,去重一定要对元素进行排序,这样我们才方便通过相邻的节点来判断是否重复了
代码如下:
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums,vector<bool>& used){
if(path.size() == nums.size()){
result.push_back(path);
return ;
}
for(int i = 0;i < nums.size();i++){
if(i > 0 && used[i-1] == false && nums[i] == nums[i-1]) continue;
if(used[i] == false){
used[i] = true;
path.push_back(nums[i]);
backtracking(nums,used);
path.pop_back();
used[i] = false;
}
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<bool> used(nums.size(),false);
sort(nums.begin(),nums.end());
backtracking(nums,used);
return result;
}
};·时间复杂度:O(n!*n)
·空间复杂度:O(n)
总结:这道题也是回溯问题中的几类问题进行汇总,所以在难度上以及逻辑理解上并不难理解
![[Flink02] Flink架构和原理](https://img-blog.csdnimg.cn/img_convert/a5c0c7ac41e553eb0021ff93cc2e99b2.png)