Problem: 51. N 皇后

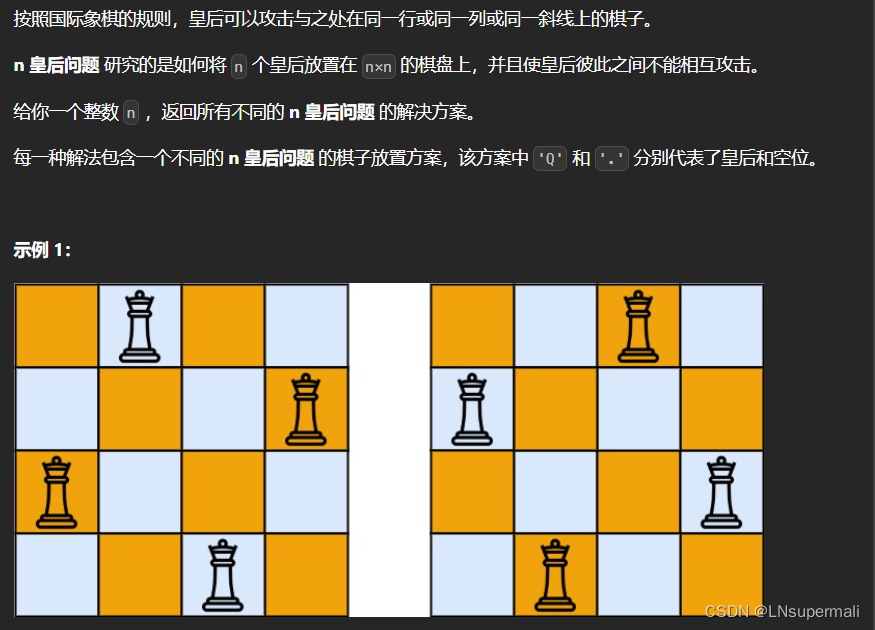
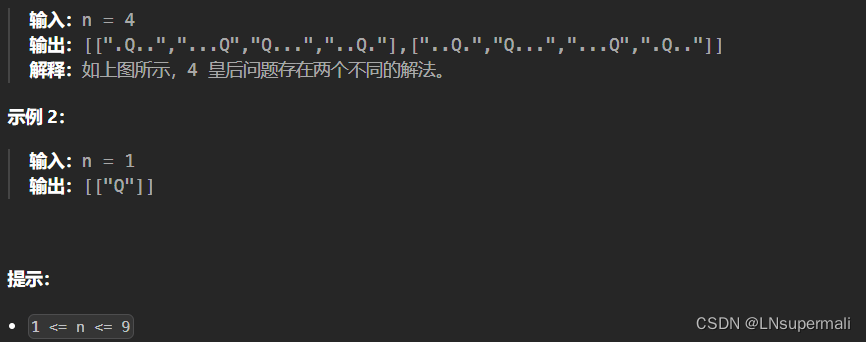
题目描述

思路

1.决策路径：board中小于row的那些行都已经成功放置了皇后；
2.选择列表：第row行的所有列都是放置皇后的选择（则根据N皇后相互攻击的股则编写判断当前决策是否合法的函数isValid）
3.结束条件：row超过board的最后一行

解决方法

1.用一个二维数组vector<vector> res;用于存储最终的所有合法结果；
2.编写回溯函数backtrack;具体实现：

2.1.触发结束条件时将当前选择列表添加到结果集合；
2.2.排除不合法选择（编写并调用isValid函数）
2.3.做选择（board[row][col] = ‘Q’）
2.4.进行下一行的决策(backtrack(board, row + 1)😉
2.5.撤销决策（board[row][col] = ‘.’;）

3.编写isValid函数：由于每次决策只用考虑到当前行和之前已经决策完的行所以在检查合法性时只用检查当前列、当前位置的右上方、当前位置的左上方

复杂度

时间复杂度:

$O(N！)$;其中$N$为棋盘的大小

空间复杂度:

$O(N^2)$

Code

class Solution {
public:
    //Result set
    vector<vector<string>> res;
    /**
     * N queen problem (Backtracking)
     *
     * @param n Given number
     * @return vector<vector<string>>
     */
    vector<vector<string>> solveNQueens(int n) {
        vector<string> board(n, string(n, '.'));
        backtrack(board, 0);
        return res;
    }

    /**
     * Backtracking logic implementation
     *
     * @param board Board
     * @param row The row of board
     */
    void backtrack(vector<string>& board, int row) {
        //End condition
        if (row == board.size()) {
            res.push_back(board);
            return;
        }

        int n = board[row].size();
        for (int col = 0; col < n; col++) {
            // Exclude illegitimate selection
            if (!isValid(board, row, col)) {
                continue;
            }
            // Make a choice
            board[row][col] = 'Q';
            // Make the next selection
            backtrack(board, row + 1);
            // Undo the selection
            board[row][col] = '.';
        }
    }

    /**
     * Judge legality
     * 
     * @param board Board
     * @param row The row of board
     * @param col The column of board
     * @return bool
     */
    bool isValid(vector<string>& board, int row, int col) {
        int n = board.size();
        // Check whether the columns have conflicting queens
        for (int i = 0; i < n; i++) {
            if (board[i][col] == 'Q') {
                return false;
            }
        }
        // Check the upper right for conflicting queens
        for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
            if (board[i][j] == 'Q') {
                return false;
            }
        }
        // Check the upper left for conflicting queens
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if (board[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }
};