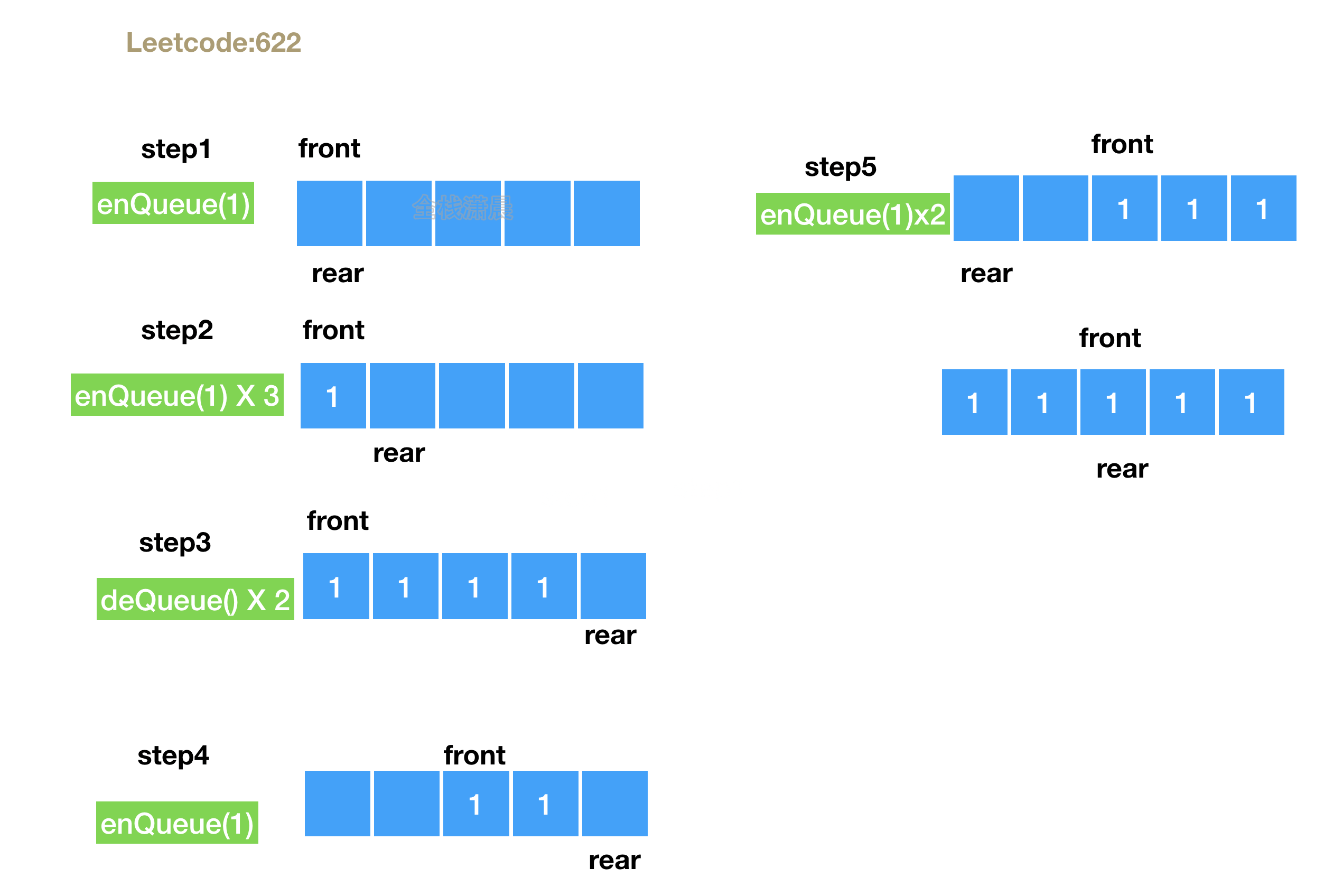
最近在复习数论，欢迎来到数论的起点gcd

最大公因数，也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个。

欧几里得算法（辗转相除法）

已知两个数a和b，求出两数的最大公约数

首先证明:

不妨设，则有(意为向下取整），令，则有。例如：11 % 2 = 11 - 5 * 2。

下面证明上式的充要性：

(1)若是的公约数，则，(能整除和)，由，则，所以也是的公约数。

(2)若是的公约数，则，，则，则也是的公约数。

综上得证和得公约数相同，故最大公约数也相同。

综上对于求解最大公约数，我们可以递归求解，直到a%b=0，此时b就是最大公约数。

int gcd(int a, int b) {
  return b ? gcd(b, a % b) : a;
}

时间复杂度O(logn)

既然是递归求解会出现栈溢出问题吗？
以下内容出自《算法竞赛入门经典》：
可以证明的是gcd函数递归层数不超过 4.785lgN+1.6723,其中 N=max{a,b}。