二叉树入门题目详解
首先知道二叉树是什么:
代码随想录 (programmercarl.com)
了解后知道其实二叉树就是特殊的链表,只是每个根节点节点都与两个子节点相连而其实图也是特殊的链表,是很多节点互相连接;这样说只是便于理解和定义,严格来说他们都是不同的数据结构了,在使用中还是要牢记各种数据结构的性质的。
二叉树的存储方式
链式的:
java
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
对于二叉树一定会第一时间想到递归,他们俩是相辅相成,互相存在的
就比如说简单的二叉树遍历就用到了递归
前序遍历:中左右
中序遍历:左中右
后序遍历:左右中
二叉树的递归遍历
// 前序遍历·递归·LC144_二叉树的前序遍历
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<Integer>();
preorder(root, result);
return result;
}
public void preorder(TreeNode root, List<Integer> result) {
if (root == null) {
return;
}
result.add(root.val);
preorder(root.left, result);
preorder(root.right, result);
}
}
// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
inorder(root, res);
return res;
}
void inorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
inorder(root.left, list);
list.add(root.val); // 注意这一句
inorder(root.right, list);
}
}
// 后序遍历·递归·LC145_二叉树的后序遍历
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
postorder(root, res);
return res;
}
void postorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
postorder(root.left, list);
postorder(root.right, list);
list.add(root.val); // 注意这一句
}
}
二叉树的层序遍历
其实可以说前边的递归遍历是深度遍历,那么层序就是字面意思,一层一层遍历,如何能一层一层遍历呢,我们想到了队列,以及父节点和子节点的关系,即先有父节点,后有子节点,子节点连着父节点,所以
当使用队列时,可以先把父节点放进去,有父节点就可以找出对应的子节点,把父节点的子节点也放进去,再把父节点输出出去,队列中剩下的就是子节点,再找到对应的子子节点,这时就可以把子节点输出出去,聪明点的已经发现了,我们现在输出的顺序就像是层序遍历,是的,层序就是这么一个过程。
这中间需要有一个用来描述此时这层节点个数的变量来中转,因为每层的节点个数都不同,
分为递归和借助队列两种方式
借助队列:更容易理解上边的过程:
class Solution {
public List<List<Integer>> resList = new ArrayList<List<Integer>>();
public List<List<Integer>> levelOrder(TreeNode root) {
checkFun02(root);
return resList;
}
//BFS--迭代方式--借助队列
public void checkFun02(TreeNode node) {
if (node == null) return;
Queue<TreeNode> que = new LinkedList<TreeNode>();
que.offer(node);
while (!que.isEmpty()) {
List<Integer> itemList = new ArrayList<Integer>();
int len = que.size();
while (len > 0) {
TreeNode tmpNode = que.poll();
itemList.add(tmpNode.val);
if (tmpNode.left != null) que.offer(tmpNode.left);
if (tmpNode.right != null) que.offer(tmpNode.right);
len--;
}
resList.add(itemList);
}
}
翻转二叉树:
其实就是使用递归先把二叉树的每个左右节点都交换一遍,再遍历一遍,得到的新的就是翻转的
java
class Solution {
/**
* 前后序遍历都可以
* 中序不行,因为先左孩子交换孩子,再根交换孩子(做完后,右孩子已经变成了原来的左孩子),再右孩子交换孩子(此时其实是对原来的左孩子做交换)
*/
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
//以后序遍历为例
invertTree(root.left); //左
invertTree(root.right); //右
swapChildren(root); //中
//虽然先遍历左右子树,但第三步到根节点时会改变其左右子树,所以仍然正确,先写中,左右,其实效果是一样的;
return root;
}
private void swapChildren(TreeNode root) {
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
}
}
对称二叉树
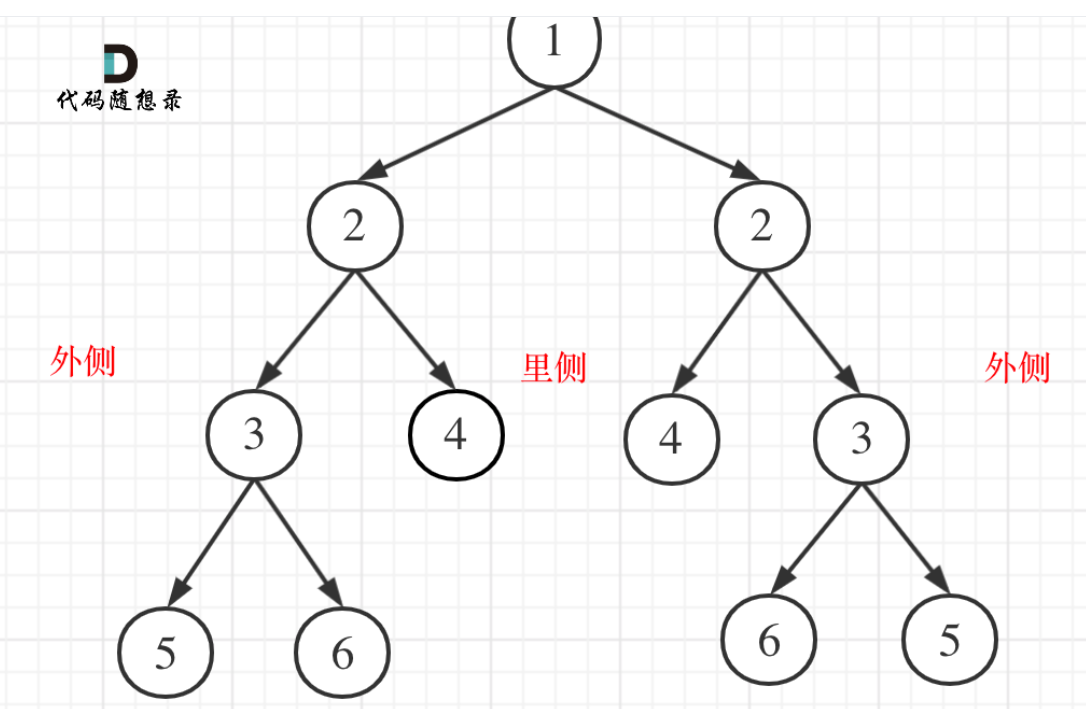
如图
我们可以想象一下后序遍历时,
左侧:5 6 3 4 2 右侧: 4 6 5 3 2 中:1
再结合图片看待,对于左子树其实是按照左右中遍历,
右子树其实可以看做左子树按照右左中的顺序遍历;
所以对于对称二叉树,可以使用后序遍历左子树,并将右子树再按照右左中的顺序遍历,若两者结果一样,那么可以判断是对称二叉树;(找规律,细微之处见斟酌)(想法很不错,现实很骨感,只有后序是不能唯一确认二叉树的);
而对于代码怎么写,是比上边的推理要麻烦一些的,因为,即使两个子树不同,只有先序遍历一种写法,是没办法唯一确认一颗二叉树的!!!
所以我们需要另想办法:再观察,其实递归遍历左子树和右子树,是将每次递归中的左右子树的左右子树对称点的值是否相同,若相同其结果就一样,所以代码条件就变成了,递归遍历二叉树并且每次递归都是带上左右子树,每次都遍历到对称的两边,左节点的子节点应始终和右节点的子节点对称,即:若左为空,右也为空,不为空时,左值应=右值;(过瘾)
java:
(每次先看了c++的代码,再看java写这种链表和二叉树的题目代码是真的复杂。。。)
class Solution {
public boolean isSymmetric(TreeNode root) {
return compare(root.left, root.right);
}
private boolean compare(TreeNode left, TreeNode right) {
if (left == null && right != null) {
return false;
}
if (left != null && right == null) {
return false;
}
if (left == null && right == null) {
return true;
}
if (left.val != right.val) {
return false;
}
// 比较外侧
boolean compareOutside = compare(left.left, right.right);
// 比较内侧
boolean compareInside = compare(left.right, right.left);
return compareOutside && compareInside;
}
}
参考c++的:
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right) {
// 首先排除空节点的情况
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
// 排除了空节点,再排除数值不相同的情况
else if (left->val != right->val) return false;
// 此时就是:左右节点都不为空,且数值相同的情况
// 此时才做递归,做下一层的判断
bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)
return isSame;
}
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
};
二叉树的最大深度

怎么求呢?直接使用递归求出根节点对应的最大高度就是该二叉树的最大深度啦
java
class solution {
/**
* 递归法
*/
public int maxDepth(TreeNode root) {
//空节点高度为0,置为return 0,则叶子结点高度一定都为1,越往上的父节点每次都加1;
if (root == null) {
return 0;
}
int leftDepth = maxDepth(root.left); //左
int rightDepth = maxDepth(root.right); //右
return Math.max(leftDepth, rightDepth) + 1; //中:高度为左右中的最大值+1;
}
}
二叉树的最小深度
方法和求最大深度有点像,又不太一样;
当只把最大改最小时会犯以下的错误。需要对节点的字节点都进行判断,当两子节点都为空时才是叶子节点;
易错点:

class Solution {
/**
* 递归法
*/
public int minDepth(TreeNode root) {
//空节点高度为0,置为return 0,则叶子结点高度一定都为1,越往上的父节点每次都加1;
if (root == null) {//意思是左右节点都为空
return 0;
}
int leftDepth = minDepth(root.left); //左
int rightDepth = minDepth(root.right); //右
if (root.left==null){// 只有左节点为空,返回的最小值只能为右节点+1
return rightDepth+1;
}
if(root.right ==null){//只有右节点为空,返回的最小值只能为左节点+1
return leftDepth+1;
}
return Math.min(leftDepth, rightDepth) + 1; //中:高度为左右中的最小值+1;
//
}
}
完全二叉树的节点个数

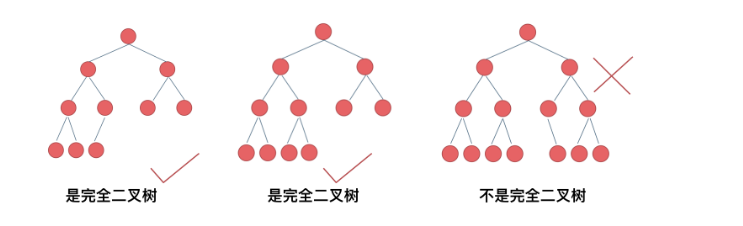
仔细思考,这道题其实和求二叉树的最大深度很类似,只不过那道题是取左右深度的最大值,这个就可以写成求左右深度+1(就是这个子树的节点个数了)
class solution {
/**
* 递归法
*/
public int Number(TreeNode root) {
//空节点高度为0,置为return 0,则叶子结点高度一定都为1,越往上的父节点每次都加1;
if (root == null) {
return 0;
}
int leftNumber = Number(root.left); //左
int rightNumber = Number(root.right); //右
return leftNumber+rightNumber + 1; //中:高度为左右中的最大值+1;
}
}