1.邮递员送信(dijkstra 不只是从起到到目标点,还要走回去)
2.炸铁路(并查集)
3.统计方形(数据加强版)(排列组合)
4.滑雪(记忆化)
5.小车问题(数学问题)
6.ACM(记忆化,搜索)
7.奶牛的耳语(二分)
8.计算器的改良(模拟)
9.L-shapes(遍历)
10.Alternating Heights(拓扑排序+二分)
邮递员送信https://www.luogu.com.cn/problem/P1629
题目描述
有一个邮递员要送东西,邮局在节点 11。他总共要送 �−1n−1 样东西,其目的地分别是节点 22 到节点 �n。由于这个城市的交通比较繁忙,因此所有的道路都是单行的,共有 �m 条道路。这个邮递员每次只能带一样东西,并且运送每件物品过后必须返回邮局。求送完这 �−1n−1 样东西并且最终回到邮局最少需要的时间。
输入格式
第一行包括两个整数,�n 和 �m,表示城市的节点数量和道路数量。
第二行到第 (�+1)(m+1) 行,每行三个整数,�,�,�u,v,w,表示从 �u 到 �v 有一条通过时间为 �w 的道路。
输出格式
输出仅一行,包含一个整数,为最少需要的时间。
输入输出样例
输入 #1复制
5 10
2 3 5
1 5 5
3 5 6
1 2 8
1 3 8
5 3 4
4 1 8
4 5 3
3 5 6
5 4 2输出 #1复制
83
说明/提示
对于 30%30% 的数据,1≤�≤2001≤n≤200。
对于 100%100% 的数据,1≤�≤1031≤n≤103,1≤�≤1051≤m≤105,1≤�,�≤�1≤u,v≤n,1≤�≤1041≤w≤104,输入保证任意两点都能互相到达。
思路:与平常最短路不同的是,这个需要走回去,那就把邻接表反过来,在走一遍dijkstra
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
const int N=1005;
int n,m;
struct node{
int to;
int w;
node(int b,int c){
to=b;
w=c;
}
};
vector<node>e1[N];
vector<node>e2[N];
int dis1[N],dis2[N];
struct s_node{
int id;
int n_dis;
s_node(int a,int b){
id=a;
n_dis=b;
}
bool operator < (const s_node &a )const{
return n_dis>a.n_dis;
}
};
void dijkstra1(){
priority_queue<s_node>q;
bool done[N];
for (int i=1;i<=n;++i){
done[i]=false;
dis1[i]=INF;
}
dis1[1]=0;
q.push(s_node(1,dis1[1]));
while (!q.empty()){
s_node u=q.top(); q.pop();
if (done[u.id]) continue;
done[u.id]=true;
for (int i=0;i<e1[u.id].size();++i){
node y=e1[u.id][i];
if (done[y.to]) continue;
if (dis1[y.to]> u.n_dis+y.w){
dis1[y.to]=u.n_dis+y.w;
q.push(s_node(y.to,dis1[y.to]));
}
}
}
}
void dijkstra2(){
priority_queue<s_node>q2;
bool done[N];
for (int i=1;i<=n;++i){
done[i]=false;
dis2[i]=INF;
}
dis2[1]=0;
q2.push(s_node(1,dis2[1]));
while (!q2.empty()){
s_node u=q2.top(); q2.pop();
if (done[u.id]) continue;
done[u.id]=true;
for (int i=0;i<e2[u.id].size();++i){
node y=e2[u.id][i];
if (done[y.to]) continue;
if (dis2[y.to]> u.n_dis+y.w){
dis2[y.to]=u.n_dis+y.w;
q2.push(s_node(y.to,dis2[y.to]));
}
}
}
}
signed main(){
cin>>n>>m;
for (int i=0;i<m;++i){
int a,b,c;
cin>>a>>b>>c;
e1[a].push_back(node(b,c));
e2[b].push_back(node(a,c));
}
dijkstra1();
int res=0;
for (int i=1;i<=n;++i){
res+=dis1[i];
}
dijkstra2();
for (int i=1;i<=n;++i){
res+=dis2[i];
}
cout<<res;
}
炸铁路https://www.luogu.com.cn/problem/P1656
题目描述
A 国派出将军 uim,对 B 国进行战略性措施,以解救涂炭的生灵。
B 国有 �n 个城市,这些城市以铁路相连。任意两个城市都可以通过铁路直接或者间接到达。
uim 发现有些铁路被毁坏之后,某两个城市无法互相通过铁路到达。这样的铁路就被称为 key road。
uim 为了尽快使该国的物流系统瘫痪,希望炸毁铁路,以达到存在某两个城市无法互相通过铁路到达的效果。
然而,只有一发炮弹(A 国国会不给钱了)。所以,他能轰炸哪一条铁路呢?
输入格式
第一行 �,� (1≤�≤150n,m (1≤n≤150,1≤�≤5000)1≤m≤5000),分别表示有 �n 个城市,总共 �m 条铁路。
以下 �m 行,每行两个整数 �,�a,b,表示城市 �a 和城市 �b 之间有铁路直接连接。
输出格式
输出有若干行。
每行包含两个数字 �,�a,b,其中 �<�a<b,表示 〈�,�〉〈a,b〉 是 key road。
请注意:输出时,所有的数对 〈�,�〉〈a,b〉 必须按照 �a 从小到大排序输出;如果�a 相同,则根据 �b 从小到大排序。
输入输出样例
输入 #1复制
6 6
1 2
2 3
2 4
3 5
4 5
5 6输出 #1复制
1 2
5 6
思路:用并查集,先每次循环去掉一个遍,然后验证一边是否成立
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
const int N=200;
int n,m;
struct node{
int from;
int to;
}a[5005];
bool cmp(const node& a, const node& b){
if (a.from==b.from) return a.to<b.to;
else return a.from<b.from;
}
int f[N],cnt=0;
int find(int x){
if (f[x]==x){
return x;
}else if (f[x]!=x){
f[x]=find(f[x]);
return f[x];
}
}
node b[5005];
void unionn(int i,int j){
f[find(i)]=find(j);
}
void check(){
for (int i=1;i<=m;++i){
for (int i=1;i<=n;++i) f[i]=i;
for (int j=1;j<=m;++j){
if (i==j)continue;
unionn(a[j].from,a[j].to);
}
for (int k=1;k<n;++k){
if (find(k)!=find(k+1)){
cnt++;
b[cnt].from=a[i].from;
b[cnt].to=a[i].to;
break;
}
}
}
for (int i=1;i<=cnt;++i){
if (b[i].from>b[i].to){
int tmp=b[i].from;
b[i].from=b[i].to;
b[i].to=tmp;
}
}
sort(b+1,b+1+cnt,cmp);
for (int i=1;i<=cnt;++i){
cout<<b[i].from<<" "<<b[i].to<<endl;
}
}
signed main(){
cin>>n>>m;
for (int i=1;i<=m;++i){
cin>>a[i].from>>a[i].to;
}
sort(a+1,a+1+m,cmp);
check();
}统计方形(数据加强版)https://www.luogu.com.cn/problem/P2241
题目背景
1997年普及组第一题
题目描述
有一个 �×�n×m 方格的棋盘,求其方格包含多少正方形、长方形(不包含正方形)。
输入格式
一行,两个正整数 �,�n,m(�≤5000,�≤5000n≤5000,m≤5000)。
输出格式
一行,两个正整数,分别表示方格包含多少正方形、长方形(不包含正方形)。
输入输出样例
输入 #1复制
2 3
输出 #1复制
8 10
思路:用数学的想法,在n×m的棋盘中,一个可以有个矩形,然后正方形的最大边长是到min{m,n},所以正方形的个数是
(n+1-i)(m+1-i)(这里假定n<m),所以矩形的数量减去正方形就是长方形的数量
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
int n,m;
signed main(){
cin>>n>>m;
int cnt=0;
int x=((n+1)*n/2)*((m+1)*m/2);
for (int i=1;i<=min(m,n);++i){
cnt+=(n-i+1)*(m-i+1);
}
cout<<cnt<<" "<<x-cnt;
}
滑雪https://www.luogu.com.cn/problem/P1434
题目描述
Michael 喜欢滑雪。这并不奇怪,因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子:
1 2 3 4 5 16 17 18 19 6 15 24 25 20 7 14 23 22 21 8 13 12 11 10 9一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度会减小。在上面的例子中,一条可行的滑坡为 24−17−16−124−17−16−1(从 2424 开始,在 11 结束)。当然 2525-2424-2323-……-33-22-11 更长。事实上,这是最长的一条。
输入格式
输入的第一行为表示区域的二维数组的行数 �R 和列数 �C。下面是 �R 行,每行有 �C 个数,代表高度(两个数字之间用 11 个空格间隔)。
输出格式
输出区域中最长滑坡的长度。
输入输出样例
输入 #1复制
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9输出 #1复制
25
说明/提示
对于 100%100% 的数据,1≤�,�≤1001≤R,C≤100。
思路:记忆化+dfs,每个点来一遍dfs,就可以找到最大长度了,记忆化可以减少时间消耗
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
const int N =105;
int a[N][N],s[N][N];
int m,n;
int dir[4][2]={{0,1},{1,0},{-1,0},{0,-1}};
void dfs(int x,int y){
if (s[x][y]) return;
s[x][y]=1;
for (int i=0;i<4;++i){
int xx=x+dir[i][0],yy=y+dir[i][1];
if (xx < 1 || xx >m || yy<1 || yy >n) continue;
if (a[x][y]>a[xx][yy]){
dfs(xx,yy);
s[x][y]=max(s[x][y],s[xx][yy]+1);
}
}
}
signed main(){
cin>>m>>n;
for (int i=1;i<=m;++i){
for (int j=1;j<=n;++j){
cin>>a[i][j];
}
}
int ans=0;
for (int i=1;i<=m;++i){
for (int j=1;j<=n;++j){
dfs(i,j);
ans=max(ans,s[i][j]);
}
}
cout<<ans;
}
小车问题https://www.luogu.com.cn/problem/P1258
题目描述
甲、乙两人同时从 A 地出发要尽快同时赶到 B 地。出发时 A 地有一辆小车,可是这辆小车除了驾驶员外只能带一人。已知甲、乙两人的步行速度一样,且小于车的速度。问:怎样利用小车才能使两人尽快同时到达。
输入格式
仅一行,三个实数,分别表示 AB 两地的距离 �s,人的步行速度 �a,车的速度 �b。
输出格式
两人同时到达 B 地需要的最短时间,保留 66 位小数。
输入输出样例
输入 #1复制
120 5 25
输出 #1复制
9.600000
说明/提示
数据规模与约定
对于 100%100% 的数据,保证 0≤�,�,�≤1090≤s,a,b≤109。
思路:解方程
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
double s,a,b;
signed main(){
cin>>s>>a>>b;
double t=((a+3*b)/(b*(3*a+b)))*s;
printf("%.6lf",t);
}
ACMhttps://www.luogu.com.cn/problem/P7793
题目背景
Zagreb 大学的团队的成员 Stjepan、Ivan 和 Gustav 正在摩洛哥参加 ACM 国际大学生程序设计竞赛的世界决赛。他们的技术指导 Goran 想出了一个无敌的策略,用于解决决赛中的题目。
题目描述
在一开始,每个团队成员迅速估计 �n 道题目中每题的难度。这些难度用 11 到 55 的数字描述,数字越大,难度也就越大。
在这之后,他们之间将分配任务。为了简单起见,任务阵列将被分成三部分,以便每个团队成员得到一个非空的连续任务序列来思考。这种分配是为了使估计的难度之和最小,而只计算被分配到该任务的团队成员的估计难度值。你的任务是计算这个最小的可能总和。
输入格式
输入共四行。
第一行输入一个整数 �n,表示问题的数量。
第二到第四行,第 �+1i+1 行 �n 个整数 ��,1,��,2,…,��,�di,1,di,2,…,di,n,表示第 �i 号成员对于这 �n 道题目估计的难度。输出格式
输出仅一行,一个整数,表示最小可能的估计难度总和。
输入输出样例
输入 #1复制
3
1 3 3
1 1 1
1 2 3输出 #1复制
4
输入 #2复制
7
3 3 4 1 3 4 4
4 2 5 1 5 5 4
5 5 1 3 4 4 4输出 #2复制
19
说明/提示
【样例 1 解释】
给第 11 号成员分配第 11 题,给第 22 号成员分配第 33 道题,给第 33 号成员分配第 22 道题。这样分配的难度总和为 1+1+2=41+1+2=4。可以证明没有难度总和更小的分配方案。
【数据范围】
对于所有数据,3⩽�⩽1.5×1053⩽n⩽1.5×105,1⩽��,�⩽51⩽di,j⩽5。
思路:动态规划,遍历所有的情况,因为一共的三个人,所以一共6种情况(需要在意顺序)确定状态转移方程:可以从上一个编号的人或自己做上一题进行转移
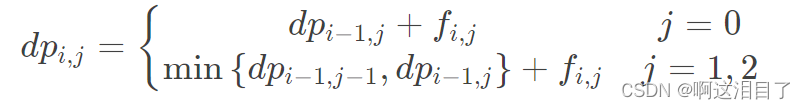
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
const int N=2e5+5;
int n,dp[4][N],f[4][N],minn=INF;
void dfs(int a,int b,int c){
memset(dp,0x3f,sizeof(dp));
dp[a][1]=f[a][1];
for (int i=2;i<=n;++i){
dp[a][i]=dp[a][i-1]+f[a][i];
dp[b][i]=min(dp[a][i-1],dp[b][i-1])+f[b][i];
dp[c][i]=min(dp[b][i-1],dp[c][i-1])+f[c][i];
}
minn=min(minn,dp[c][n]);
}
signed main(){
cin>>n;
for (int i=1;i<=3;++i){
for (int j=1;j<=n;++j){
cin>>f[i][j];
}
}
dfs(1,2,3);
dfs(1,3,2);
dfs(2,1,3);
dfs(2,3,1);
dfs(3,2,1);
dfs(3,1,2);
cout<<minn;
}奶牛的耳语https://www.luogu.com.cn/problem/P1296
题目描述
在你的养牛场,所有的奶牛都养在一排呈直线的牛栏中。一共有 �n 头奶牛,其中第 �i 头牛在直线上所处的位置可以用一个整数坐标 ��(0≤��≤108)pi(0≤pi≤108) 来表示。在无聊的日子里,奶牛们常常在自己的牛栏里与其它奶牛交流一些八卦新闻。每头奶牛发出的声音响度是一样的,而由于声波的能量衰减,某头奶牛发出的声音只能被与它距离不超过 �(0≤�≤104)d(0≤d≤104) 的奶牛所听到,这样这对奶牛就称为可以相互交流的。现在给出所有奶牛的位置和声音所能传播的最远距离 �d ,请你编个程序来计算你的养牛场里究竟有多少对可以相互交流的奶牛。
输入格式
第一行包含两个整数 �,�n,d。
第二行包含 �n 个整数,每个整数都是一个坐标 ��pi,描述一头奶牛在直线上的位置。
输出格式
一个数,表示养牛场中可以相互交流奶牛的对数。
输入输出样例
输入 #1复制
5 10
10 12 16 37 40输出 #1复制
4
说明/提示
数据规模
对于 40%40% 的数据,1≤�≤1031≤n≤103。
对于 100%100% 的数据,1≤�≤1061≤n≤106。
思路:运用二分的思想,先对数组排序,然后用二分找到第一个听不见的位置,然后,加到计数器里面
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
const int N=1e6+5;
int n,d,a[N];
signed main(){
cin>>n>>d;
for (int i=1;i<=n;++i) cin>>a[i];
sort(a+1,a+1+n);
int ans=0;
for (int i=1;i<=n;++i){
int p=upper_bound(a+i+1,a+1+n,a[i]+d)-a;
ans+=p-i-1;
}
cout<<ans;
}计算器的改良https://www.luogu.com.cn/problem/P1022
题目背景
NCL 是一家专门从事计算器改良与升级的实验室,最近该实验室收到了某公司所委托的一个任务:需要在该公司某型号的计算器上加上解一元一次方程的功能。实验室将这个任务交给了一个刚进入的新手 ZL 先生。
题目描述
为了很好的完成这个任务,ZL 先生首先研究了一些一元一次方程的实例:
4+3�=84+3x=8。
6�−5+1=2−2�6a−5+1=2−2a。
−5+12�=0−5+12y=0。
ZL 先生被主管告之,在计算器上键入的一个一元一次方程中,只包含整数、小写字母及
+、-、=这三个数学符号(当然,符号“-”既可作减号,也可作负号)。方程中并没有括号,也没有除号,方程中的字母表示未知数。你可假设对键入的方程的正确性的判断是由另一个程序员在做,或者说可认为键入的一元一次方程均为合法的,且有唯一实数解。
输入格式
一个一元一次方程。
输出格式
解方程的结果(精确至小数点后三位)。
输入输出样例
输入 #1复制
6a-5+1=2-2a
输出 #1复制
a=0.750
思路:模拟
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
const int N=100;
int l;
double x,flag,mid,a[N];
char c,p;
signed main(){
l=1,flag=1;
while (c!='='){
c=getchar();
if (c=='+'){
flag=1;
l++;
}else if (c=='-'){
flag=-1;
l++;
}
if (c>='0' && c<='9'){
if (a[l]==0){
a[l]+=(c-'0')*flag;
}else{
a[l]=a[l]*10+(c-'0')*flag;
}
}
if (c>='a' && c<='z'){
p=c;
if (a[l]==0) x+=flag;
else x+=a[l];
a[l]=0;
l--;
}
}
mid=l,l++,flag=1;
while (c!='\n'){
c=getchar();
if (c=='+'){
flag=1;
l++;
}else if (c=='-'){
flag=-1;
l++;
}
if (c>='0' && c<='9'){
if (a[l]==0){
a[l]+=(c-'0')*flag;
}else{
a[l]=a[l]*10+(c-'0')*flag;
}
}
if (c>='a' && c<='z'){
p=c;
if (a[l]==0) x-=flag;
else x-=a[l];
a[l]=0;
l--;
}
}
int sum=0;
for (int i=1;i<=l;++i){
if (i<=mid){
sum-=a[i];
}else {
sum+=a[i];
}
}
if (!(sum/x)){
printf("%c=0.000",p);
}else {
printf("%c=%.3lf",p,sum/x);
}
}L-shapeshttps://www.luogu.com.cn/problem/CF1722F
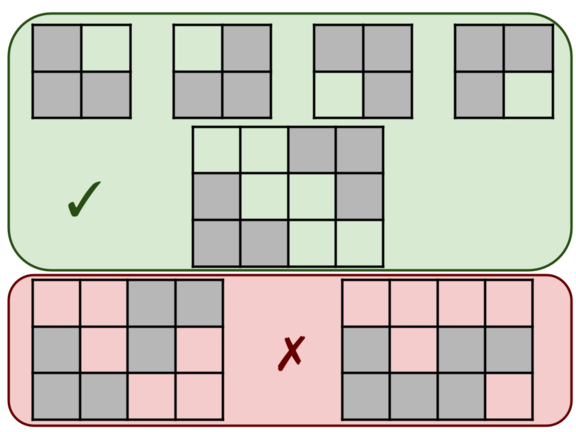
题目描述
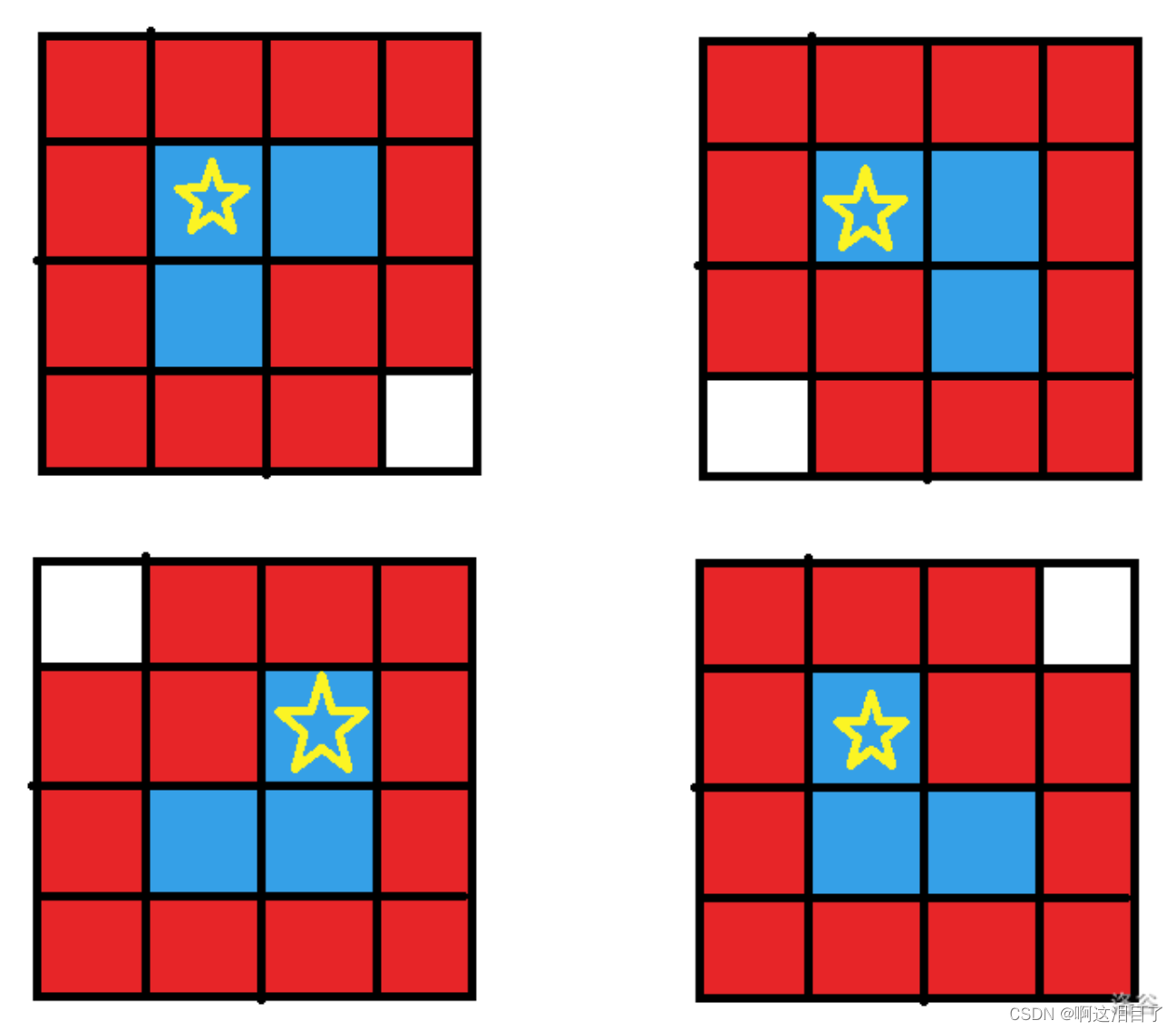
An L-shape is a figure on gridded paper that looks like the first four pictures below. An L-shape contains exactly three shaded cells (denoted by *), which can be rotated in any way.
You are given a rectangular grid. Determine if it contains L-shapes only, where L-shapes can't touch an edge or corner. More formally:
- Each shaded cell in the grid is part of exactly one L-shape, and
- no two L-shapes are adjacent by edge or corner.
For example, the last two grids in the picture above do not satisfy the condition because the two L-shapes touch by corner and edge, respectively.
输入格式
The input consists of multiple test cases. The first line contains an integer �t ( 1≤�≤1001≤t≤100 ) — the number of test cases. The description of the test cases follows.
The first line of each test case contains two integers �n and �m ( 1≤�,�≤501≤n,m≤50 ) — the number of rows and columns in the grid, respectively.
Then �n lines follow, each containing �m characters. Each of these characters is either '.' or '*' — an empty cell or a shaded cell, respectively.
输出格式
For each test case, output "YES" if the grid is made up of L-shape that don't share edges or corners, and "NO" otherwise.
You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).
题意翻译
L形在网格纸上形如下面的前四张图片。L形正好包含三个阴影单元(用*表示),可以以任何方式旋转。
现给你一个矩形网格。确定它是否仅包含L形,其中L形不能接触边或角,也就是说网格中的每个阴影单元正好是一个L形的一部分,并且没有两个L形通过边或角相邻。
例如,上图中的最后两个网格不满足条件,因为两个L形分别通过角和边缘接触。
如果网格满足条件,则输出“YES”,否则输出“NO”。
输入输出样例
输入 #1复制
10 6 10 ........** .**......* ..*..*.... .....**... ...*.....* ..**....** 6 10 ....*...** .**......* ..*..*.... .....**... ...*.....* ..**....** 3 3 ... *** ... 4 4 .*.. **.. ..** ..*. 5 4 .*.. **.. .... ..** ..*. 3 2 .* ** *. 2 3 *.. .** 3 2 .. ** *. 3 3 .** *.* **. 3 3 ..* .** ..*输出 #1复制
YES NO NO NO YES NO NO YES NO NO
思路:把*都成1,其他都是0,找到特殊的四种情况,然后判断,把可以成立的变成0,最后遍历一边数组,如果还有1那就不行
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
const int N=55;
int t,n,m,a[N][N];
void check(int i,int j){
if (a[i+1][j] && a[i+1][j+1] && !a[i-1][j-1] && !a[i-1][j] && !a[i-1][j+1] && !a[i][j-1] && !a[i][j+1] && !a[i][j+2]
&& !a[i+1][j-1] && !a[i+1][j+2] && !a[i+2][j-1] && !a[i+2][j] && !a[i+2][j+1] && !a[i+2][j+2])
{
a[i][j]=a[i+1][j] = a[i+1][j+1] = 0;
return;
}
if (a[i][j+1] && a[i+1][j+1] && !a[i-1][j-1] && !a[i-1][j] && !a[i-1][j+1] && !a[i-1][j+2] && !a[i][j-1] && !a[i][j+2]
&& !a[i+1][j-1] && !a[i+1][j] && !a[i+1][j+2] && !a[i+2][j] && !a[i+2][j+1] && !a[i+2][j+2])
{
a[i][j+1]=a[i+1][j+1] = a[i][j] = 0;
return;
}
if (a[i+1][j] && a[i+1][j-1] && !a[i-1][j-1] && !a[i-1][j] && !a[i-1][j+1] && !a[i][j-2] && !a[i][j-1] && !a[i][j+1]
&& !a[i+1][j-2] && !a[i+1][j+1] && !a[i+2][j-1] && !a[i+2][j] && !a[i+2][j+1] && !a[i+2][j-2])
{
a[i+1][j]=a[i+1][j-1] = a[i][j] = 0;
return;
}
if (a[i][j+1] && a[i+1][j] && !a[i-1][j-1] && !a[i-1][j] && !a[i-1][j+1] && !a[i-1][j+2] && !a[i][j-1] && !a[i][j+2]
&& !a[i+1][j-1] && !a[i+1][j+1] && !a[i+1][j+2]&& !a[i+2][j-1] && !a[i+2][j] && !a[i+2][j+1] )
{
a[i][j]=a[i+1][j] = a[i][j+1] = 0;
return;
}
}
signed main(){
cin>>t;
while (t--){
cin>>n>>m;
memset(a,0,sizeof(a));
for (int i=1;i<=n;++i){
for (int j=1;j<=m;++j){
char c; cin>>c;
if (c=='*') a[i][j]=1;
}
}
for (int i =1 ;i<=n ;++i ){
for (int j =1 ; j<=m ;++ j){
if (a[i][j] == 1) check(i,j);
}
}
bool flag=true;
for (int i =1 ;i<=n ;++i ){
for (int j =1 ; j<=m ;++ j){
if (a[i][j] == 1){
flag=false;
break;
}
}
if (!flag) break;
}
if (!flag) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
}Alternating Heightshttps://www.luogu.com.cn/problem/P10050
题目描述
Troy 计划给 CCO 的学生拍一张合影,他向你寻求帮助。
有 �K 个学生,编号从 11 到 �K。Troy 忘记了学生的身高,但他记得没有两个学生的身高相同。
Troy 有一个序列 �1,�2,…,��A1,A2,…,AN,表示合影中从左到右的学生顺序。一个学生可能在 �A 中出现多次。你不确定这张合影会怎么拍,但你不愿意认为 Troy 犯了错误。
Troy 会给你 �Q 个形式为 �,�x,y 的询问,每个询问为「给定学生序列 ��,��+1,…,��Ax,Ax+1,…,Ay,他们的身高能否形成一个交替序列?」更具体地说,我们用 ℎ�hi 表示第 �i 个学生的身高。如果存在一种身高分配ℎ1,ℎ2,…,ℎ�h1,h2,…,hK,使得 ℎ��>ℎ��+1<ℎ��+2>ℎ��+3<…ℎ��hAx>hAx+1<hAx+2>hAx+3<…hAy,回答
YES;否则回答NO。注意,每个查询都是独立的:也就是说,询问 �i 的身高分配与询问 �j 的身高分配无关 (�≠�)(i=j)。
输入格式
第一行包含三个用空格分隔的整数 �,�N,K 和 �Q。
第二行包含 �N 个整数,表示 �1,�2,…,��(1≤��≤�)A1,A2,…,AN(1≤Ai≤K)。
接下来的 �Q 行,每行包含两个用空格分隔的整数 �x 和 �(1≤�<�≤�)y(1≤x<y≤N),表示一组查询。
输出格式
输出 �Q 行。第 �i 行,输出
YES或者NO,表示 Troy 的第 �i 个查询的答案。输入输出样例
输入 #1复制
6 3 3
1 1 2 3 1 2
1 2
2 5
2 6输出 #1复制
NO
YES
NO说明/提示
样例说明
对于第一个询问,不可能有 ℎ1>ℎ1h1>h1,所以答案是
NO。对于第二个询问,ℎ1>ℎ2<ℎ3>ℎ1h1>h2<h3>h1 的一种方案是 ℎ1=160 cm,ℎ2=140 cm,ℎ3=180 cmh1=160 cm,h2=140 cm,h3=180 cm。另一种方案是 ℎ1=1.55 m,ℎ2=1.473 m,ℎ3=1.81 mh1=1.55 m,h2=1.473 m,h3=1.81 m。
对于第三个询问,不可能同时有 ℎ1>ℎ2h1>h2 和 ℎ1<ℎ2h1<h2。
数据范围
对于所有的数据,有 2≤�≤30002≤N≤3000,2≤�≤�2≤K≤N,1≤�≤1061≤Q≤106。
子任务编号
分值
�N
�K
�Q
11
1616
2≤�≤30002≤N≤3000
�=2K=2
1≤�≤1061≤Q≤106
22
2424
2≤�≤5002≤N≤500
2≤�≤min(�,5)2≤K≤min(N,5)
1≤�≤1061≤Q≤106
33
2828
2≤�≤30002≤N≤3000
2≤�≤�2≤K≤N
1≤�≤20001≤Q≤2000
44
3232
2≤�≤30002≤N≤3000
2≤�≤�2≤K≤N
1≤�≤1061≤Q≤106
思路:看成图,如果存在环,那就无法成立,用拓扑排序判断是否成环,暴力搜会超时,用二分的思想,固定左端点,然后找到以此为左端点的最大区间长度
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
const int N=3005;
int n,k,Q,a[N],in[N],num[N],g[N][N],max_len[N];
queue<int>q;
bool check(int l,int r){ //拓扑排序
int sum=0;
memset(in,0,sizeof(in)); //记录入度
memset(num,0,sizeof(num)); //记录相邻的节点数
while (!q.empty()) q.pop();
for (int i=l+1;i<=r;i+=2){ //指向高的
if (i-1>0){
g[a[i]][++num[a[i]]]=a[i-1];
in[a[i-1]]++;
}
if (i+1<=r){
g[a[i]][++num[a[i]]]=a[i+1];
in[a[i+1]]++;
}
}
for (int i=1;i<=k;++i){ //入度为0就入队
if (!in[i]) q.push(i);
}
while (!q.empty()){
int p=q.front(); q.pop();
sum++;
for (int i=1;i<=num[p];++i){
in[g[p][i]]--; //出队后,相邻点的入度减1
if (!in[g[p][i]]) q.push(g[p][i]);
}
}
return sum==k;
}
int erfen(int m){
int l=m,r=n,maxn=0;
while (l<=r){
int mid=l+r>>1;
if (check(m,mid)){ //以m为左端点的最长区间
maxn=max(maxn,mid);
l=mid+1;
}
else r=mid-1;
}
return maxn;
}
signed main(){
cin>>n>>k>>Q;
for (int i=1;i<=n;++i) cin>>a[i];
for (int i=1;i<=n;++i) max_len[i]=erfen(i);
for (int i=1;i<=Q;++i){
int x,y;
cin>>x>>y;
if (max_len[x]<y) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
}