【数据结构】无向图创建邻接矩阵、深度优先遍历和广度优先遍历（C语言版）

news2024/11/25 0:26:06
无向图创建邻接矩阵、深度优先遍历和广度优先遍历
  • 一、概念解析：
    • （1）无向图：
    • （2）邻接矩阵：
  • 二、创建邻接矩阵：
  • 三、深度遍历、广度遍历
    • （1）深度遍历概念：
    • （2）广度遍历概念：
  • 四、实例展示

一、概念解析：

（1）无向图：

假设图G由两个集合V和E组成，记为G={V , E}。其中V是顶点的有限集合，E是连接V中两个不同顶点的边的有限集合。如果E中的顶点对是有序的，即E中的每条边都是有方向的，则称G是有向图。如果顶点对是无序的，则称G是无向图

在这里插入图片描述

在这里插入图片描述

（2）邻接矩阵：

邻接矩阵主要由：二维数组 实现

如图
在这里插入图片描述

转换成邻接矩阵为：

在这里插入图片描述

二、创建邻接矩阵：

基本每一步都有注释，详细观看，建议画图理解

代码如下：

#define MAXSIZE 100 
//	邻接矩阵 
typedef struct Matrix{
	
	int V_Data;		//	顶点数据域 
	int E_Data;		//	边数数据域
	
	int Node[MAXSIZE];	//	存放顶点数据，也就是顶点表 
	int Weight[MAXSIZE][MAXSIZE]; 	//	存放权重，为矩阵中两点有边的标记符号 
	
}MaTrix,*MATRIX;

//	邻接矩阵数据结构体 
typedef struct Edge{
	
	int v1;		//	用来存放第一个顶点 
	int v2;		//	用来存放第二个顶点
	int weight;	//	用来存放两点之间的标记符，即为权 
}*EDGE;

//******************** 邻接矩阵*******************//
//	邻接矩阵、顶点和边初始化 
void Init_Matrix(MATRIX S,int Vertex)
{	
	S->E_Data = 0;			//	初始化为0条边 
	S->V_Data = Vertex;		//	初始化顶点数 
	
	int i,j;
	for(i=0;i<Vertex;i++)
	{
		for(j=0;j<Vertex;j++)
		{
			S->Weight[i][j] = 0;
		}
	} 
}

//	开始插入边的权重，即为两个顶点之间边的标记符
void InSerData(MATRIX S,EDGE E)
{
	//	将输入的顶点v1、v2之间的边，用权作为标记，在矩阵中表示
	//	这里是无向图，所以边没有方向，需要做标记两次（为v1-v2和v2-v1） 
	S->Weight[E->v1][E->v2] = E->weight;	 
	S->Weight[E->v2][E->v1] = E->weight; 
} 

//	开始插入数据 
void InSerEdge_Data(MATRIX S,int edge,int V)
{
	int i,j;
	
	if(edge>0)	//	边数大于0的时候才插入数据 
	{
		printf("请输入顶点和权重(空格分隔!)\n");
		for(i=0;i<edge;i++)
		{		
			EDGE E;				//分配内存，接受顶点v1,v2和权重（标记符）	
			E = (EDGE)malloc(sizeof(struct Edge));	
			
			scanf("%d %d %d",&(E->v1),&(E->v2),&(E->weight));
			
			if(E->v1 ==E->v2)
			{
				printf("无向图邻接矩阵对角线为0,输入错误,结束运行\n");
				exit(-1); 
			}
			
			InSerData(S,E);
		}	
		printf("请输入要定义的顶点，填入顶点表中: \n");
		for(j=0;j<V;j++)
		{
			scanf("%d",&(S->Node[j]));
		}		
	
	}else{	
		printf("输入的边数错误"); 
	} 		
}

三、深度遍历、广度遍历

（1）深度遍历概念：

在这里插入图片描述

在这里插入图片描述

定义的结构体、数组可看上面代码

深度遍历代码解析：

//*****************	深度优先遍历算法—邻接矩阵 *****************//
void DFS_Begin(MATRIX P,int k,int V)
{
	int i;
	flag[k] = 1;	//标记当前顶点，表示已经遍历过

	printf("%d ",P->Node[k]);	//	输出当前顶点 
	
	for(i=0;i<V;i++)
	{
		if(!flag[i] && P->Weight[k][i] != 0)//	如果当前顶点的邻近点存在，且没有遍历过 
		{									//	则继续递归遍历 
		
			DFS_Begin(P,i,V);		//	递归遍历当前顶点的邻近点 
		}	
	} 
}

void Init_DFSMatrix(MATRIX P,int V)
{
	int i;
	//	初始化标记符数组，全为0 
	for(i=0;i<V;i++)
	{
		flag[i] = 0;
	}
	
	for(i=0;i<V;i++)	//	每个顶点都要检查是否遍历到 
	{
		if(!flag[i])	//	排除遇到已经遍历的顶点
			DFS_Begin(P,i,V);		//	开始深度遍历	
	} 
	putchar('\n');	
}

（2）广度遍历概念：

在这里插入图片描述

这里使用到了链队列（也可以使用数组队列，看个人想法），可以看我之前的博文有讲：

//******************** 队列 *****************//
typedef struct Queue{
	
	int data[MAXSIZE];	//	队列大小 
	int head;	//	队头 
	int wei;	//	队尾 
	
}Queue; 

//*****************	队列 *************************************//
//	队列初始化 
void InitQueue(Queue *q)
{
	q->head= 0;		//	初始化队头、队尾 
	q->wei = 0;
} 

//	判断队列是否为空
int EmptyQueue(Queue *q)
{
	if(q->head == q->wei)
		return 1;
	else{
		return 0;
	}		
} 

//	入队
void PushQueue(Queue *q,int t)
{
	if((q->wei+1)%MAXSIZE == q->head)	//	说明队列已经满了
		return;
	else{	
		q->data[q->wei] = t;	
		q->wei = (q->wei +1)%MAXSIZE;	//	队尾后移 
	}
		 
} 

//	出队
void PopQueue(Queue *q,int *x)
{
	if(q->wei == q->head)	//	出队完毕 
		return;	
	else{	 	
		*x = q->data[q->head];
		q->head = (q->head + 1)%MAXSIZE; //	队头后移	
	}	
	
} 
 
//***************** 广度优先搜索算法—邻接矩阵 ****************//
void Init_Bfs(MATRIX S,int V)
{
	int i,j;
	int k;
	 
	Queue Q;
	
	for(i=0;i<V;i++)
	{
		Vist[i] = 0;	//	初始化标记符 
	}
	
	InitQueue(&Q);	//	队列初始化 
	
	for (i = 0; i < V; i++)
	{
		if (!Vist[i])	//	判断以这个顶点为基准，有连接的其他顶点 
		{
			Vist[i] = 1;	//	标记遍历的这个顶点 
			printf("%d ", S->Node[i]);
		
			PushQueue(&Q, i);	//	入队 

			while (!EmptyQueue(&Q))	//	队列中还有数据，说明这个顶点连接的其他顶点还没有遍历完 
			{
				PopQueue(&Q,&i);	//	出队 
				
				for (j = 0; j < V; j++)
				{
					//	以这个顶点为基准，遍历其他连接的顶点 
					if (!Vist[j] && S->Weight[i][j] != 0)
					{
						Vist[j] = 1;	//	与之连接的顶点作上标记，便于后序顶点跳过相同的遍历 
						printf("%d ", S->Node[j]);//	输出与之相邻连接的顶点 
						PushQueue(&Q, j);	//	让与之连接的顶点其位置入队 
					}
				}
			}
		}
	}
}

四、实例展示

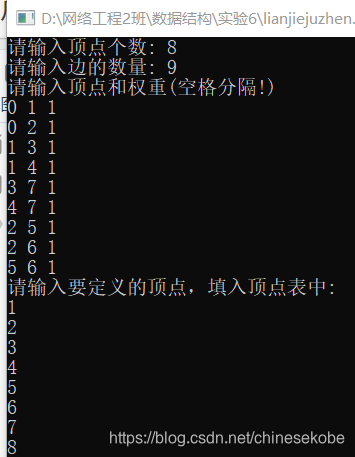
注意：这里存入数据时，坐标点以原点（0,0）为起点开始！

以这个图为样例展示：

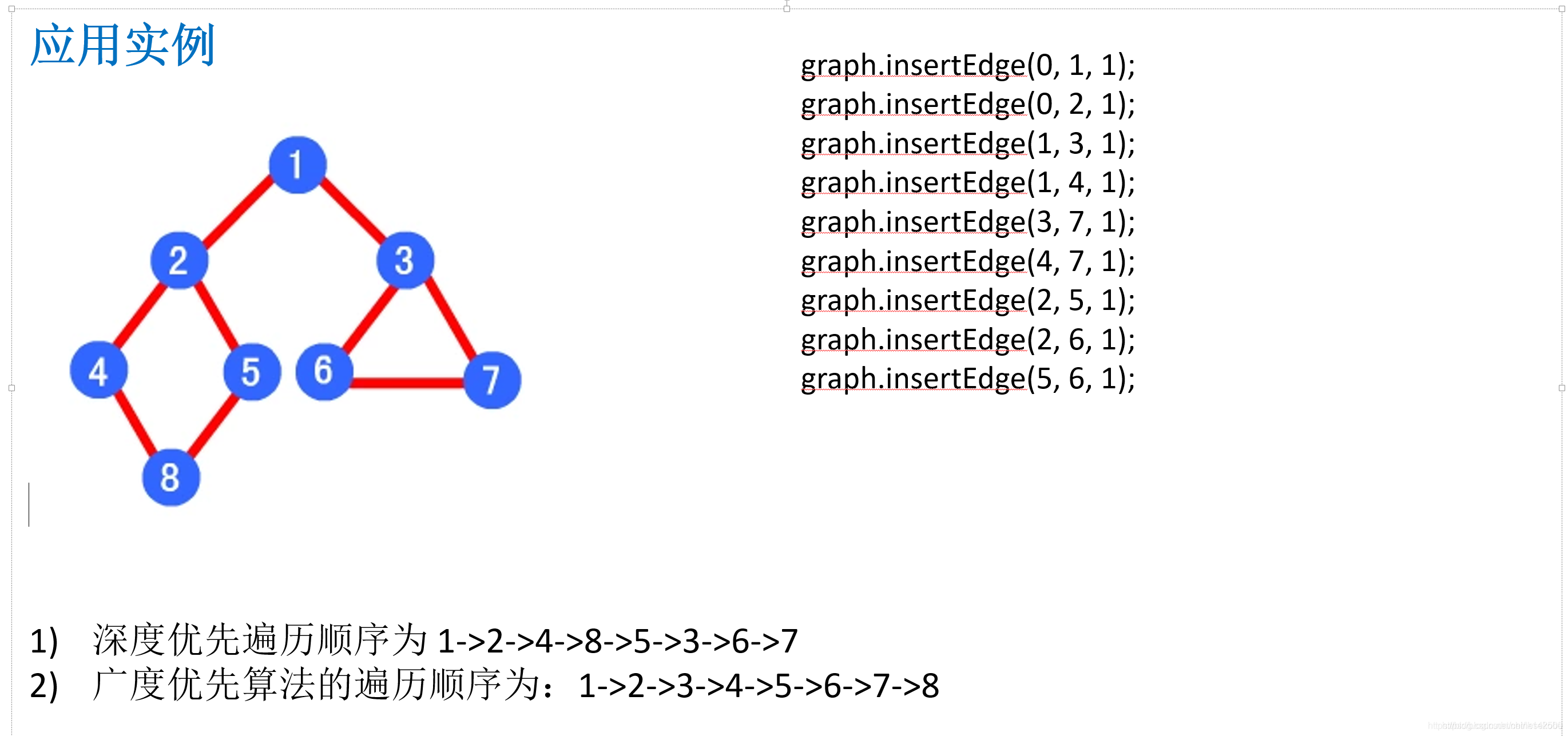
在这里插入图片描述

全部代码：

#include<stdio.h>
#include<stdlib.h>

#define MAXSIZE 100 

//	深度遍历标记符
int flag[MAXSIZE]; 		//	邻接矩阵 

//	广度优先遍历标记符 
int Vist[MAXSIZE]; 		//	邻接矩阵

//******************** 队列 *****************//
typedef struct Queue{
	
	int data[MAXSIZE];	//	队列大小 
	int head;	//	队头 
	int wei;	//	队尾 
	
}Queue; 

//	邻接矩阵 
typedef struct Matrix{
	
	int V_Data;		//	顶点数据域 
	int E_Data;		//	边数数据域
	
	int Node[MAXSIZE];	//	存放顶点数据，也就是顶点表 
	int Weight[MAXSIZE][MAXSIZE]; 	//	存放权重，为矩阵中两点有边的标记符号 
	
}MaTrix,*MATRIX;

//	邻接矩阵数据结构体 
typedef struct Edge{
	
	int v1;		//	用来存放第一个顶点 
	int v2;		//	用来存放第二个顶点
	int weight;	//	用来存放两点之间的标记符，即为权 
}*EDGE;

//******************** 邻接矩阵*******************//
//	邻接矩阵、顶点和边初始化 
void Init_Matrix(MATRIX S,int Vertex)
{	
	S->E_Data = 0;			//	初始化为0条边 
	S->V_Data = Vertex;		//	初始化顶点数 
	
	int i,j;
	for(i=0;i<Vertex;i++)
	{
		for(j=0;j<Vertex;j++)
		{
			S->Weight[i][j] = 0;
		}
	} 
}

//	开始插入边的权重，即为两个顶点之间边的标记符
void InSerData(MATRIX S,EDGE E)
{
	//	将输入的顶点v1、v2之间的边，用权作为标记，在矩阵中表示
	//	这里是无向图，所以边没有方向，需要做标记两次（为v1-v2和v2-v1） 
	S->Weight[E->v1][E->v2] = E->weight;
	 
	S->Weight[E->v2][E->v1] = E->weight; 
} 

//*****************	深度优先遍历算法—邻接矩阵 *****************//
void DFS_Begin(MATRIX P,int k,int V)
{
	int i;
	flag[k] = 1;	//标记当前顶点，表示已经遍历过

	printf("%d ",P->Node[k]);	//	输出当前顶点 
	
	for(i=0;i<V;i++)
	{
		if(!flag[i] && P->Weight[k][i] != 0)//	如果当前顶点的邻近点存在，且没有遍历过 
		{									//	则继续递归遍历 
		
			DFS_Begin(P,i,V);		//	递归遍历当前顶点的邻近点 
		}	
	} 
}

void Init_DFSMatrix(MATRIX P,int V)
{
	int i;
	//	初始化标记符数组，全为0 
	for(i=0;i<V;i++)
	{
		flag[i] = 0;
	}
	
	for(i=0;i<V;i++)	//	每个顶点都要检查是否遍历到 
	{
		if(!flag[i])	//	排除遇到已经遍历的顶点
			DFS_Begin(P,i,V);		//	开始深度遍历	
	} 
	putchar('\n');
	
	
}

//*****************	队列 *************************************//
//	队列初始化 
void InitQueue(Queue *q)
{
	q->head= 0;		//	初始化队头、队尾 
	q->wei = 0;
} 

//	判断队列是否为空
int EmptyQueue(Queue *q)
{
	if(q->head == q->wei)
		return 1;
	else{
		return 0;
	}		
} 

//	入队
void PushQueue(Queue *q,int t)
{
	if((q->wei+1)%MAXSIZE == q->head)	//	说明队列已经满了
		return;
	else{	
		q->data[q->wei] = t;	
		q->wei = (q->wei +1)%MAXSIZE;	//	队尾后移 
	}
		 
} 

//	出队
void PopQueue(Queue *q,int *x)
{
	if(q->wei == q->head)	//	出队完毕 
		return;	
	else{
		 	
		*x = q->data[q->head];
		q->head = (q->head + 1)%MAXSIZE; //	队头后移
	
	}	
	
	
} 
 
//***************** 广度优先搜索算法—邻接矩阵 ****************//
void Init_Bfs(MATRIX S,int V)
{
	int i,j;
	int k;
	 
	Queue Q;
	
	for(i=0;i<V;i++)
	{
		Vist[i] = 0;	//	初始化标记符 
	}
	
	InitQueue(&Q);	//	队列初始化 
	
	for (i = 0; i < V; i++)
	{
		if (!Vist[i])	//	判断以这个顶点为基准，有连接的其他顶点 
		{
			Vist[i] = 1;	//	标记遍历的这个顶点 
			printf("%d ", S->Node[i]);
		
			PushQueue(&Q, i);	//	入队 

			while (!EmptyQueue(&Q))	//	队列中还有数据，说明这个顶点连接的其他顶点还没有遍历完 
			{
				PopQueue(&Q,&i);	//	出队 
				
				for (j = 0; j < V; j++)
				{
					//	以这个顶点为基准，遍历其他连接的顶点 
					if (!Vist[j] && S->Weight[i][j] != 0)
					{
						Vist[j] = 1;	//	与之连接的顶点作上标记，便于后序顶点跳过相同的遍历 
						printf("%d ", S->Node[j]);//	输出与之相邻连接的顶点 
						PushQueue(&Q, j);	//	让与之连接的顶点其位置入队 
					}
				}
			}
		}
	}
} 

//	初始化顶点个数 
int Init_Vertex()
{
	int Vertex;
				 
	printf("请输入顶点个数: ");
	scanf("%d",&Vertex);
	return Vertex;
}

//	初始化边的数量 
int Init_Edge()
{
	int edge;
	printf("请输入边的数量: ");
	scanf("%d",&edge);
	return edge;
		
} 

//	开始插入数据 
void InSerEdge_Data(MATRIX S,int edge,int V)
{
	int i,j;
	
	if(edge>0)	//	边数大于0的时候才插入数据 
	{
		printf("请输入顶点和权重(空格分隔!)\n");
		for(i=0;i<edge;i++)
		{		
			EDGE E;				//分配内存，接受顶点v1,v2和权重（标记符）	
			E = (EDGE)malloc(sizeof(struct Edge));	
			
			scanf("%d %d %d",&(E->v1),&(E->v2),&(E->weight));
			
			if(E->v1 ==E->v2)
			{
				printf("无向图邻接矩阵对角线为0,输入错误,结束运行\n");
				exit(-1); 
			}
			
			InSerData(S,E);
		}	
		printf("请输入要定义的顶点，填入顶点表中: \n");
		for(j=0;j<V;j++)
		{
			scanf("%d",&(S->Node[j]));
		}
		
	
	}else{
		
		printf("输入的边数错误"); 
	} 
		
} 

//	打印无向图邻接矩阵 
void Show_Matrix(MATRIX p,int Vertex)
{
	int i,j;
	for(i=0;i<Vertex;i++)
	{
		for(j=0;j<Vertex;j++)
		{
			printf("%4d",p->Weight[i][j]);	//	打印邻接矩阵 
		}	
			putchar('\n');	//	换行 
	}
}

int main()
{
	
	int val;
	int Vertex;
	int edge;
	
	MATRIX p;		//	邻接矩阵头节点指针

	//	创建无向图邻接矩阵 					
	Vertex = Init_Vertex();
	edge = Init_Edge();
				
	p = (MATRIX)malloc(sizeof(MaTrix));		//分配内存空间 
				
	p->V_Data = Vertex;		//	记录顶点个数 
	p->E_Data = edge;		//	记录边的个数 
				
	Init_Matrix(p,Vertex);	//	初始化邻接矩阵 
				
	InSerEdge_Data(p,edge,Vertex);	//	插入数据 
				
	//	打印无向图的邻接矩阵 
	printf("无向图邻接矩阵如下:");	
	printf("\n----------------------------------\n\n");
	Show_Matrix(p,Vertex);
	printf("\n----------------------------------\n");
	
	//	深度优先遍历—邻接矩阵	
	printf("深度遍历—邻接矩阵结果为:\n");
	Init_DFSMatrix(p,Vertex);
	
	//	广度优先遍历—邻接矩阵
	printf("广度优先遍历—邻接矩阵结果为: \n");
	Init_Bfs(p,Vertex);
				
	return 0;	
}

结果图：
在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1451749.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

模型 IPO(输入、处理、输出)学习模型

模型 IPO(输入、处理、输出)学习模型

系列文章 分享 模型&#xff0c;了解更多&#x1f449; 模型_总纲目录。重在提升认知。信息转化与传递。 1 模型 IPO(输入、处理、输出)学习模型的应用 1.1 项目管理知识体系 PMBOK 中的IPO应用 在项目管理领域&#xff0c;PMBOK&#xff08;Project Management Body of Know…
阅读更多...
ChatGPT绘图指南：DALL.E3玩法大全(一)

ChatGPT绘图指南：DALL.E3玩法大全(一)

一、 DALLE.3 模型介绍 1、什么是 DALLE.3 模型&#xff1f; DALLE-3模型&#xff0c;是一种由OpenAI研发的技术&#xff0c;它是一种先进的生成模型&#xff0c;可以将文字描述转化为清晰的图片。这种模型的名称"DALLE"实际上是"Deep Auto-regressive Latent …
阅读更多...
云计算基础-存储虚拟化（深信服aSAN分布式存储）

云计算基础-存储虚拟化（深信服aSAN分布式存储）

什么是存储虚拟化 分布式存储是利用虚拟化技术 “池化”集群存储卷内通用X86服务器中的本地硬盘&#xff0c;实现服务器存储资源的统一整合、管理及调度&#xff0c;最终向上层提供NFS、ISCSI存储接口&#xff0c;供虚拟机根据自身的存储需求自由分配使用资源池中的存储空间。…
阅读更多...
AcWing 1235. 付账问题（贪心）

AcWing 1235. 付账问题（贪心）

[题目概述] 几个人一起出去吃饭是常有的事。 但在结帐的时候&#xff0c;常常会出现一些争执。 现在有 n 个人出去吃饭&#xff0c;他们总共消费了 S 元。 其中第 i 个人带了 a i a_i ai​ 元。 幸运的是&#xff0c;所有人带的钱的总数是足够付账的&#xff0c;但现在问题来…
阅读更多...
计算机网络——13P2P应用

计算机网络——13P2P应用

P2P应用 纯P2P架构 没有&#xff08;或极少&#xff09;一直运行额服务器任意端系统都可以直接通信利用peer的服务能力Peer节点间歇上网&#xff0c;每次IP地址都有可能变化 例子&#xff1a; 文件分发流媒体VoIP 文件分发&#xff1a;C/S vs P2P 问题&#xff1a;从一台…
阅读更多...
《Go 简易速速上手小册》第2章：控制结构与函数（2024 最新版）

《Go 简易速速上手小册》第2章：控制结构与函数（2024 最新版）

文章目录 2.1 条件语句&#xff1a;决策的艺术2.1.1 基础知识讲解2.1.2 重点案例&#xff1a;用户角色权限判断实现用户角色权限判断扩展功能实现代码功能扩展&#xff1a;添加或删除用户 2.1.3 拓展案例 1&#xff1a;成绩等级判断实现成绩等级判断功能实现代码扩展功能&#…
阅读更多...
Spring中的事务实现、失效场景即AOP的相关概念理解

Spring中的事务实现、失效场景即AOP的相关概念理解

spring实现事务&#xff08;声明式事务&#xff09;的本质就是aop完成的,它会对方法的前后进行拦截,在执行方法之前开启事务,在执行完目标方法之后根据执行情况提交或回滚事务。aop就是面向切面编程&#xff0c;在spring中将那些与业务无关&#xff0c;但却对多个对象产生影响的…
阅读更多...
Opencv简单图像操作

Opencv简单图像操作

Opencv 一、读取图片 1.imshow Mat imread(const string& filename, intflags1 );flags: enum { /* 8bit, color or not */CV_LOAD_IMAGE_UNCHANGED -1, /* 8bit, gray */CV_LOAD_IMAGE_GRAYSCALE 0, /* ?, color */CV_LOAD_IMAGE_COLOR 1, /* any depth, ? */…
阅读更多...
深度学习之线性模型

深度学习之线性模型

深度学习之线性模型 y w * x模型思路 y w * x b模型思路 y w * x模型 思路 这里求权重w , 求最适合的权重&#xff0c;就是求损失值最小的时候 这里用穷举法:在一个范围内&#xff0c;列出w的所有值&#xff0c;并且计算出每组数据的平均损失值,以w 为横坐标, 损失值为纵坐…
阅读更多...
定时器按秒计时

定时器按秒计时

一、函数学习 二、代码、 main.c #include "stm32f10x.h" // Device header #include "Delay.h" #include "OLED.h" #include "Timer.h"uint16_t Num;int main(void) {OLED_Init();Timer_Init(); OLED_ShowString(1,1,"Num:…
阅读更多...
树莓派5 EEPROM引导加载程序恢复镜像

树莓派5 EEPROM引导加载程序恢复镜像

树莓派5不能正常启动&#xff0c;可以通过电源led灯的闪码来判断错误发生的大致情形。 LED警告闪码 如果树莓派由于某种原因无法启动&#xff0c;或者不得不关闭&#xff0c;在许多情况下&#xff0c;LED会闪烁特定的次数来指示发生了什么。LED会闪烁几次长闪烁&#xff0c;然…
阅读更多...
Linux POSIX信号量 线程池

Linux POSIX信号量 线程池

Linux POSIX信号量 线程池 一. 什么是POSIX信号量&#xff1f;二. POSIX信号量实现原理三. POSIX信号量接口函数四. 基于环形队列的生产消费模型五. 线程池 一. 什么是POSIX信号量&#xff1f; POSIX信号量是一种用于同步和互斥操作的机制&#xff0c;属于POSIX&#xff08;Po…
阅读更多...
C++入门篇——命名空间

C++入门篇——命名空间

在C/C中&#xff0c;变量、函数和后面要学到的类都是大量存在的&#xff0c;这些变量、函数和类的名称将都存 在于全局作用域中&#xff0c;可能会导致很多冲突。使用命名空间的目的是对标识符的名称进行本地化&#xff0c; 以避免命名冲突或名字污染&#xff0c;namespace关键…
阅读更多...
Calendar的使用(Java)

Calendar的使用(Java)

直接从需求来理解&#xff1a;将2024年2月16日增加一个月 如果不使用Calendar的话&#xff0c;我们需要定义字符串记住这个日期&#xff0c;然后把字符串解析成Date日期对象&#xff0c;通过Date日期对象获取其毫秒值&#xff0c;然后增加一个月的毫秒值&#xff0c;再格式化时…
阅读更多...
社区养老|社区养老服务系统|基于springboot社区养老服务系统设计与实现(源码+数据库+文档)

社区养老|社区养老服务系统|基于springboot社区养老服务系统设计与实现(源码+数据库+文档)

社区养老服务系统目录 目录 基于springboot社区养老服务系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、管理员部分功能 &#xff08;1&#xff09; 用户管理 &#xff08;2&#xff09;服务种类管理 &#xff08;3&#xff09;社区服务管理 &#xff08…
阅读更多...
嵌入式培训机构四个月实训课程笔记（完整版）-Linux ARM驱动编程第五天-ARM Linux编程之字符设备驱动（物联技术666）

嵌入式培训机构四个月实训课程笔记（完整版）-Linux ARM驱动编程第五天-ARM Linux编程之字符设备驱动（物联技术666）

链接&#xff1a;https://pan.baidu.com/s/1V0E9IHSoLbpiWJsncmFgdA?pwd1688 提取码&#xff1a;1688 教学内容&#xff1a; 1、内核模块的简单框架&#xff1a; __init __exit执行完后就释放空间 简单框架&#xff1a;包含三个部分 1&#xff09;模块初始化和模块退出函数…
阅读更多...
题目：3.神奇的数组（蓝桥OJ 3000）

题目：3.神奇的数组（蓝桥OJ 3000）

问题描述&#xff1a; 解题思路&#xff1a; 官方&#xff1a; 我的总结&#xff1a; 利用双指针遍历每个区间并判断是否符合条件&#xff1a;若一个区间符合条件则该区间在其左端点不变的情况下的每一个子区间都符合条件&#xff0c;相反若一个区间内左端点固定情况下有一个以…
阅读更多...
排序算法---桶排序

排序算法---桶排序

原创不易&#xff0c;转载请注明出处。欢迎点赞收藏~ 桶排序&#xff08;Bucket Sort&#xff09;是一种排序算法&#xff0c;它将待排序的数据分到几个有序的桶中&#xff0c;每个桶再分别进行排序&#xff0c;最后将各个桶中的数据按照顺序依次取出&#xff0c;即可得到有序序…
阅读更多...
MySQL免安装版安装教程

MySQL免安装版安装教程

官网下载安装包 MySQL :: Download MySQL Community Server (Archived Versions) 选择mysql版本下载 安装配置MySQL 将下载完的Mysql安装包解压到指定目录 打开windos系统的cmd&#xff0c;以管理员身份运行 进入mysql文件夹中的bin目录 安装MySQL的服务mysqld --install 初…
阅读更多...
【教程】C++语言基础学习笔记（五）——Vector向量

【教程】C++语言基础学习笔记（五）——Vector向量

写在前面&#xff1a; 如果文章对你有帮助&#xff0c;记得点赞关注加收藏一波&#xff0c;利于以后需要的时候复习&#xff0c;多谢支持&#xff01; 【C语言基础学习】系列文章 第一章 《项目与程序结构》 第二章 《数据类型》 第三章 《运算符》 第四章 《流程控制》 第五章…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023