这里写目录标题
- 高斯消元
- 高斯消元求线性方程组
- 用途
- 高斯消元的数学思想
- 例题+代码
- 二级目录
- 一级目录
- 二级目录
- 二级目录
- 二级目录
- 一级目录
- 二级目录
- 二级目录
- 二级目录
- 一级目录
- 二级目录
- 二级目录
- 二级目录
- 一级目录
- 二级目录
- 二级目录
- 二级目录
高斯消元
高斯消元求线性方程组
用途

这个算法可以以n的三次方的时间复杂度来求一个线性方程组的解(即x1,x2,x3,…,xn)
但是同时要注意,方程组的解有三种情况,上图
例子:
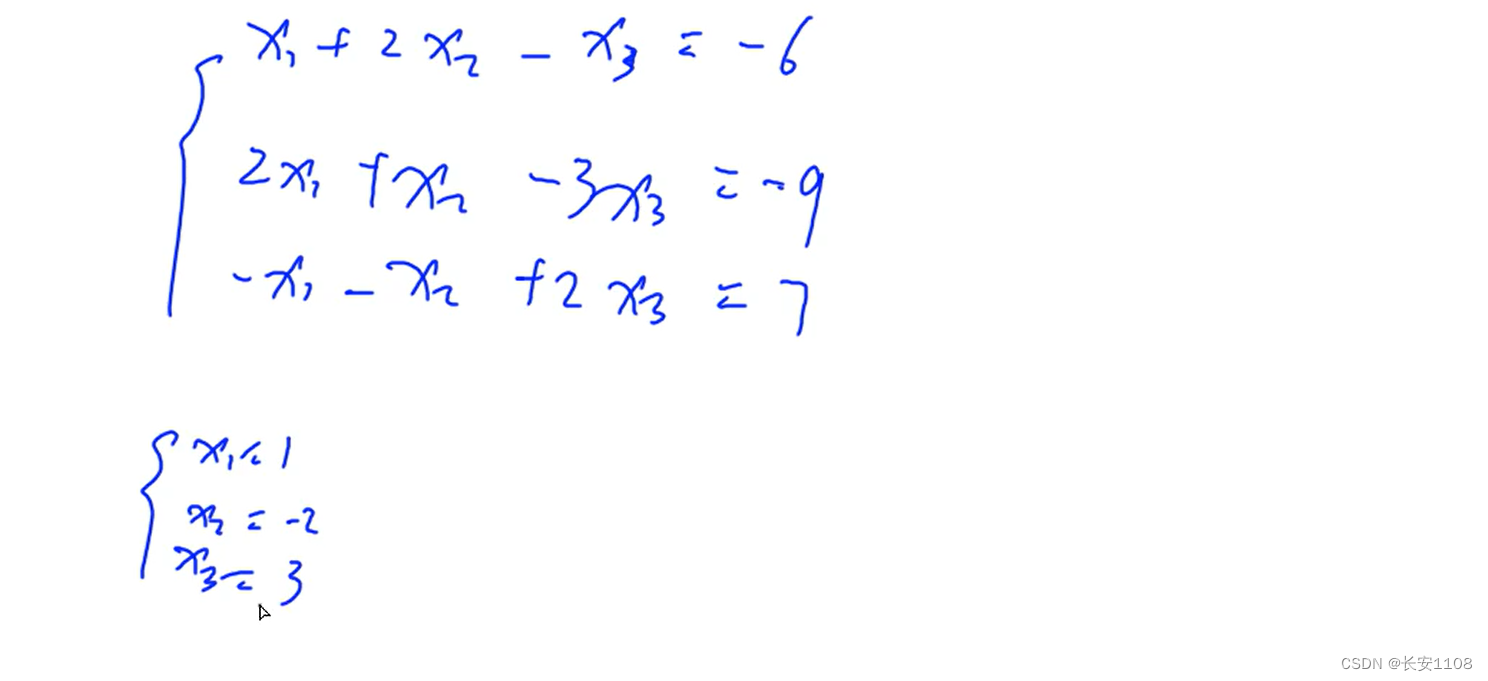
输入n*(n+1)个数,其中每一行包含n个系数以及一个等式右边的答案,一共有n行
最后输出x1到xn
高斯消元的数学思想
将系数抽出来,组成一个矩阵,之后对矩阵做初等行列变化,化为最简阶梯型矩阵,最后化为上三角,如下图所示

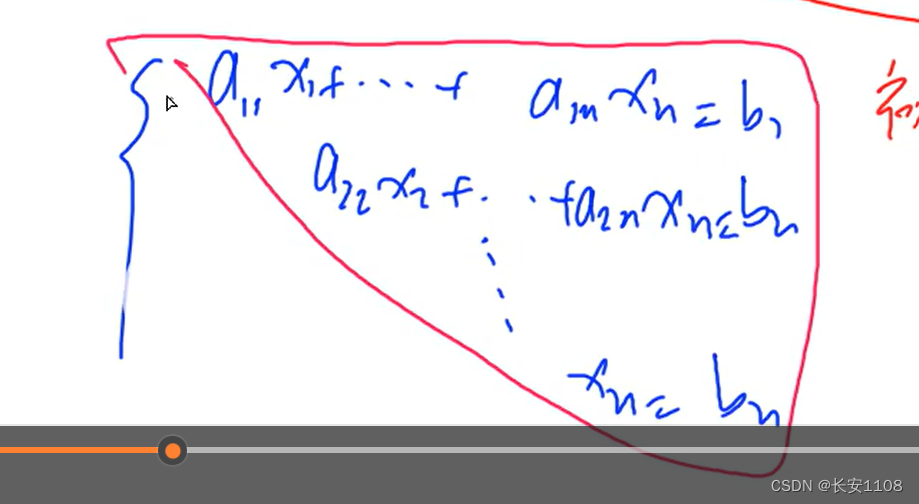
关于解的情况,有三种:
在推上三角的过程中
如果最后能化成完美三角形,那就是有唯一解
如果最后出现0=非零,那么就是有矛盾,就是无解
如果最后出现了恒等方程,也就是能消去一个方程,或者说n个未知数,但是只有小于n个解,那么就是无穷解

具体的步骤以及最后的结果:

具体高斯消元的数学思想可以看视频《数学知识(三)》的20-36分钟
例题+代码
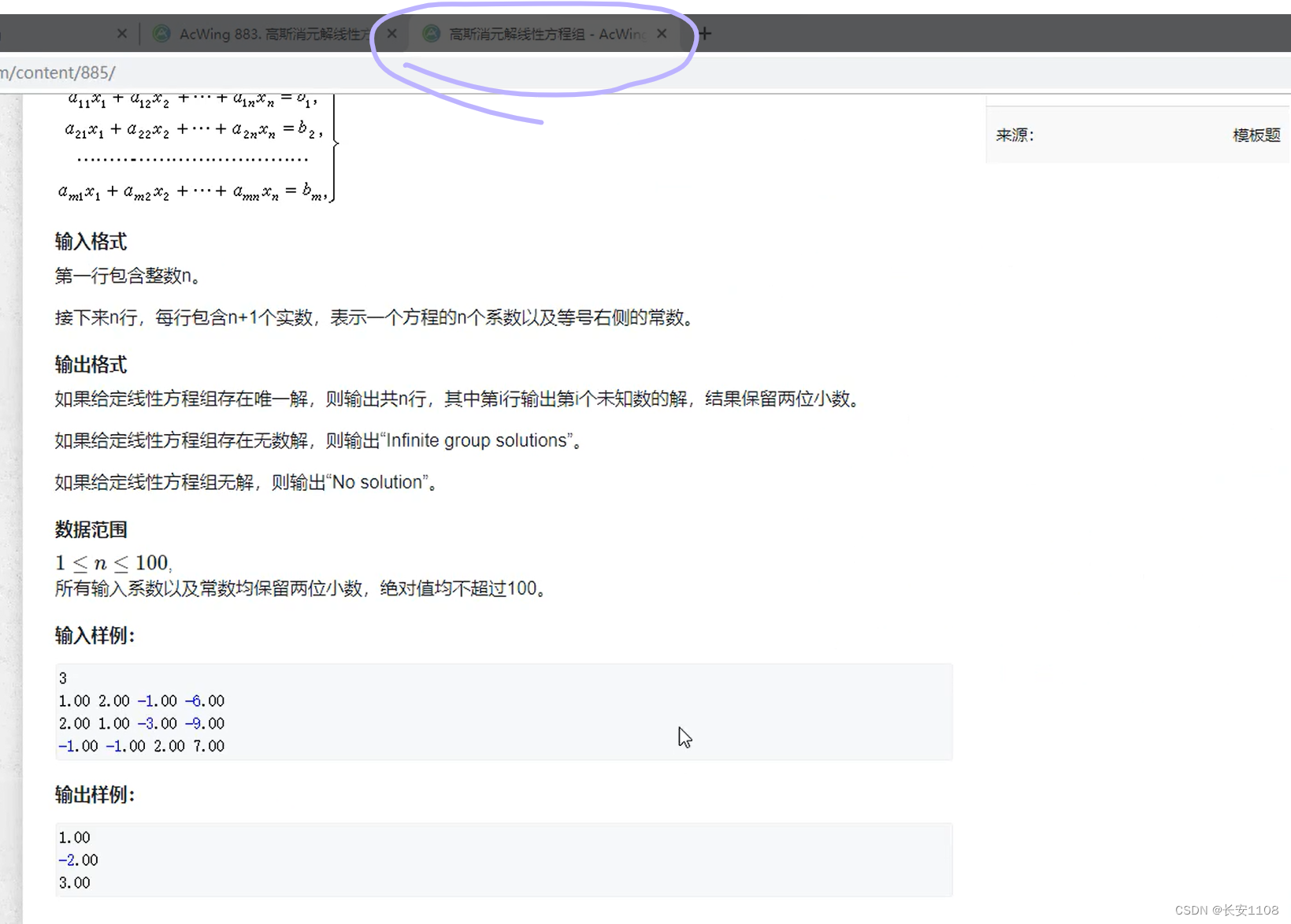
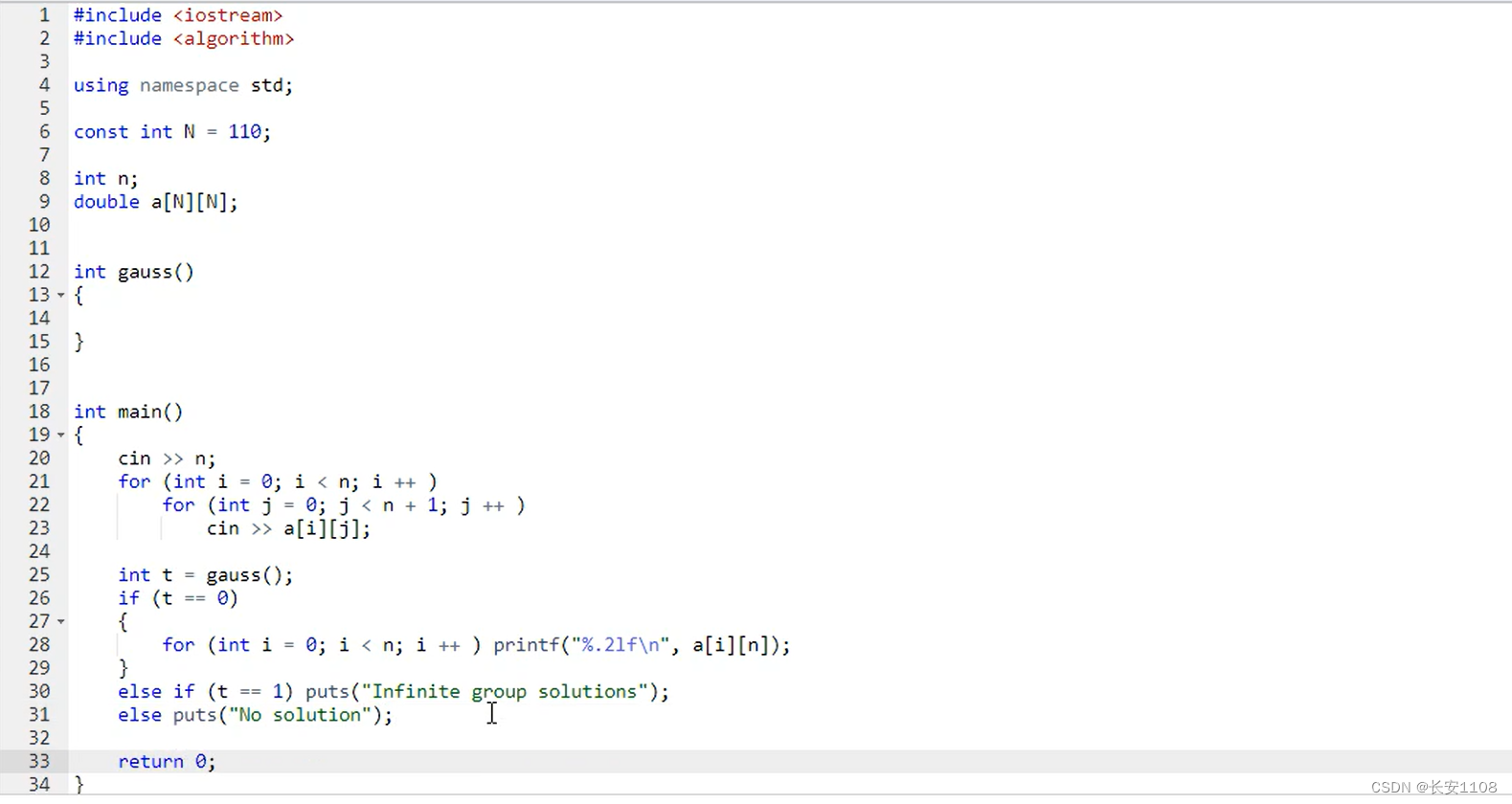
最后的数据都存放在了a[i][n]种,即最后一列的所有行,也就是等式右边的那些值,tips:保留两位小数,%.2lf,在%lf之前加一个.2

数据分析:
定义一个n,表示有几行,也就是有几个解
之后a数组用来存储输入数据,即所有的系数和等式右边的数
eps=1e-6,因为浮点数数据有误差,他的0不是真正的0,而是0.000000…1,所以需要用小于一个特别小的数来表示是0
在gauss函数里:
c代表当前列,r代表当前行
之后,for循环中初始化c和r都是0,然后遍历c,(初始化r为0,是用来动态设置当前的“顶行位置”,只有当前这个大的for循环快要结束时,r才会++)
在每一步遍历中,都是在c行下进行的
进行第一步:
先定义一个t,初始化为r,用来存当前列的绝对值最大值数的行号
之后一个for循环,用来找到当前列的绝对值最大的行:i从r开始遍历下面的所有行,如果fabs(a[i][c])>fabs(a[t][c]),那么i就是目前来说最大的行号,将t更新为i。tip:fabs(x),返回x的绝对值,并且是浮点类型,包含头文件cmath
之后拿到 t 之后,特判一下,如果fabs(a[t][c] < eps) 那么就是0,continue一下,因为是0的话就不用其他操作了
进行第二步:(将该行换到最上面)
定义i从c循环到小于等于n,交换a[t][i],a[r][i]
进行第三步:(将该行第一个数变成1)
注意这一步要倒着进行循环,因为每一次操作都要用到a[r][c],所以要在最后一次循环之前保证a[r][c]是不变的,同时注意此时不再是t行,而是r行,因为第二步时已经换到第一行了
定义i从n到大于等于c,i–,a[r][i] /= a[r][c]
进行第四步:(将下面所有的行的数变成0)
for循环定义i从r+1开始,循环到小于n,因为当前是在r,所以从r+1开始
判断如果a[i][c] >eps,即a[i][c]不是0,再进行后续操作
后续操作:(开始变为0,与第三步思想相同,等式左右同时进行数学变换,使得第c列下面的数都是0)
for循环定义 j 从n到大于等于c,j–
(此时i代表行号,j代表i行目前的列号)
a[i][j] -= a[r][j]*a[i][c]
当前行遍历列的所有的数,都更新为自己减去第一行当前列的数 乘以 当前行第一个数
最后r++;for循环结束
然后判断如果r<n,也就是最后方程数小于解的个数,那么有两种解的情况,
for循环,i 从 r 到 小于n,表示要判断那些没有用到的方程,(i表示行)
之后每次循环判断是否有a[i][n] > eps,即a[i][n]不是0,如果有,就是无解,返回2
for循环结束,返回1,表示有无穷个解
最后如果没有r<n,整个gauss函数返回0即表示有唯一解
但是返回0之前,要对答案进行化简求解,就是上图中的最后一个for循环







![BUUCTF misc 专题(47)[SWPU2019]神奇的二维码](https://img-blog.csdnimg.cn/f5b4278a7ed54b81b250d6807299e460.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAdHRfbnBj,size_20,color_FFFFFF,t_70,g_se,x_16)