目录
洛谷P1328 [NOIP2014 提高组] 生活大爆炸版石头剪刀布
题目背景
题目描述
输入格式
输出格式
输入输出样例
说明/提示
题目分析
代码示例
洛谷2080增进感情
题目背景
题目描述
输入格式
输出格式
输入输出样例
说明/提示
数据范围与约定
题目分析
代码示例
洛谷P1328 [NOIP2014 提高组] 生活大爆炸版石头剪刀布
题目背景
NOIP2014 提高组 D1T1
题目描述
石头剪刀布是常见的猜拳游戏:石头胜剪刀,剪刀胜布,布胜石头。如果两个人出拳一样,则不分胜负。在《生活大爆炸》第二季第 8 集中出现了一种石头剪刀布的升级版游戏。
升级版游戏在传统的石头剪刀布游戏的基础上,增加了两个新手势:
斯波克:《星际迷航》主角之一。
蜥蜴人:《星际迷航》中的反面角色。
这五种手势的胜负关系如表一所示,表中列出的是甲对乙的游戏结果。
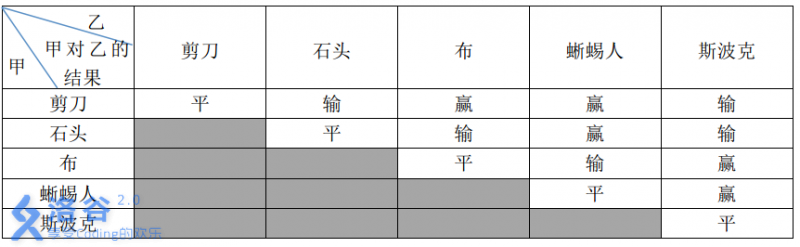
现在,小 A 和小 B 尝试玩这种升级版的猜拳游戏。已知他们的出拳都是有周期性规律的,但周期长度不一定相等。例如:如果小 A 以 石头-布-石头-剪刀-蜥蜴人-斯波克 长度为 66 的周期出拳,那么他的出拳序列就是 石头-布-石头-剪刀-蜥蜴人-斯波克-石头-布-石头-剪刀-蜥蜴人-斯波克-...,而如果小 B 以 剪刀-石头-布-斯波克-蜥蜴人 长度为 55 的周期出拳,那么他出拳的序列就是 剪刀-石头-布-斯波克-蜥蜴人-剪刀-石头-布-斯波克-蜥蜴人-...。
已知小 A 和小 B 一共进行 N 次猜拳。每一次赢的人得 11 分,输的得 00 分;平局两人都得 0 分。现请你统计 N 次猜拳结束之后两人的得分。
输入格式
第一行包含三个整数:N,NA,NB,分别表示共进行 N 次猜拳、小 A 出拳的周期长度,小 B 出拳的周期长度。数与数之间以一个空格分隔。
第二行包含 NA 个整数,表示小 A 出拳的规律,第三行包含 NB 个整数,表示小 B 出拳的规律。其中,0表示 剪刀,1表示 石头,2表示 布,3 表示 蜥蜴人,4表示 斯波克。数与数之间以一个空格分隔。
输出格式
输出一行,包含两个整数,以一个空格分隔,分别表示小 A、小 B 的得分。
输入输出样例
输入 #1复制
10 5 6 0 1 2 3 4 0 3 4 2 1 0
输出 #1复制
6 2
输入 #2复制
9 5 5 0 1 2 3 4 1 0 3 2 4
输出 #2复制
4 4
说明/提示
对于 100%100% 的数据,0<N≤200,0<NA≤200,0<NB≤200 。
题目分析
1,这题模拟的话用switch写的话挺麻烦的,(或许其他方法没想到),所以这里从大佬那学会了新思路
2,首先得到一个得分表(对于表中灰色的部分自己补充完整)
int a[210],b[210],sco[5][5]={{0,0,1,1,0},{1,0,0,1,0},{0,1,0,0,1},{0,0,1,0,1},{1,1,0,0,0}};//得分表
3。接下来开始循环统计 (表中每一个单元格代表甲对乙的结果先统计谁的得分就把谁当做甲)甲的出拳序列是存在不同的行,而乙是不同的列
4,注意周期的变化,因为有周期性,为了避免复杂,所以这里用%来解决周期性
代码示例
#include<bits/stdc++.h>
using namespace std;
int a[210],b[210],sco[5][5]={{0,0,1,1,0},{1,0,0,1,0},{0,1,0,0,1},{0,0,1,0,1},{1,1,0,0,0}};//得分表特别注意
int main(){
int k,m,n;
int suma=0,sumb=0;
cin>>k>>m>>n;
for(int i=0;i<m;i++)
cin>>a[i];
for(int i=0;i<n;i++)
cin>>b[i];
for(int i=0;i<k;i++)
{
suma+=sco[a[i%m]][b[i%n]];//周期性,%保证他在这个范围里变化
sumb+=sco[b[i%n]][a[i%m]];//这里与上面的行列坐标不一样是因为要统计b所以把b看成甲。自然甲就存放在行坐标了
}
cout<<suma<<' '<<sumb<<endl;
}
洛谷2080增进感情
题目背景
小明和小红的感情,是慢慢发展起来的。
题目描述
他们对对方分别有一个好感值。定义两人的亲密程度为两人的好感值之和。
如果他们的亲密程度达到 v,则他们将走到一起。他们以后的生活将取决于两人的好感值之差的绝对值,这个值越小,他们的生活将越幸福。
现在,他们对对方的好感值都为 00,小明有 n 件事可以干,每件事可以增加他对小红的好感 ai 点,并且增加小红对他的好感 bi 点。(可能为负数)
小明可以任选一些事做,请你帮小明求出怎样才能让他们的生活更加幸福(求出两人在一起的前提下,好感值之差的最小绝对值即可)。
输入格式
第一行,两个正整数 n,v。
之后 n 行,每行两个空格隔开的整数 ai,bi。
输出格式
一行,一个非负整数,表示两人在一起的前提下,好感值之差的最小绝对值。如果无论如何两人也无法在一起,输出 -1。
输入输出样例
输入 #1复制
4 15 5 6 -1 8 7 2 1 0
输出 #1复制
3
说明/提示
数据范围与约定
- 对于 20%20% 数据,保证 n≤10。
- 对于 100%100% 数据,保证 1≤n≤30,1≤∣ai∣,∣bi∣≤100。
题目分析
1.这题目考的是搜索,但总有种01背包的感觉,得考虑取或不取
2,根据题目发现dfs算法可以用在这进行搜索,考虑dfs函数的构建,首先,有个返回条件就是minn=0时,就不必再往后重复算了,因为这肯定是绝对值中最小了,然后就是进行minn的改变,那啥时才能对minn改变呢就是当他俩相加符合规定的亲密度(保证在一起)时对minn进行改变(还有个前提条件就是保证现在所有事情都考虑过取和不取的情况了,此时考虑事情数应该大于能做的事情数,相等是代表你现在正在考虑第n件事)
代码示例
#include<bits/stdc++.h>
using namespace std;
int minn=1e9,n,v,a[110],b[110];
void dfs(int x,int y,int p)
{
if(minn==0)//剪枝
{
return ;
}
if(p>n)//全考虑完后决定最小值
{ if(x+y>=v)//保证在一起所以加起来的亲密度得大于规定的
minn=min(minn,abs(x-y));//找最小值
return;
}
dfs(x+a[p],y+b[p],p+1);//考虑做的情况
dfs(x,y,p+1);//不做的情况
return ;
}
int main()
{
cin>>n>>v;
for(int i=1; i<=n; i++)cin>>a[i]>>b[i];
dfs(0,0,1);//好感从0开始
if(minn<1e9)cout<<minn<<' ';
else cout<<-1;
}
以上如果有不足之处,还望大佬指出错误