文章目录
- 3. 数组
- 3.1 数组的概述
- 3.2 一维数组的使用
- 3.2.1 一维数组初始化
- 3.2.2 一维数组内存解析
- 3.3 多维数组的使用
- 3.3.1 多维数组初始化
- 3.3.2 多维数组的注意事项:
- 3.3.3 int[] x,y[]
- 3.3.4 多维数组的内存解析
- 3.4 数组中涉及到的常见算法
- 3.4.1 线性查找
- 3.4.2 二分法查找算法
- 3.4.3 排序算法
- 3.4.3.1 十大内部排序算法
- 3.4.2 算法特点概述
- 3.4.4 快速排序
- 快排思想
- 快排的时间复杂度
- 1.最好时间复杂度:
- 2.最坏时间复杂度
- 3.平均时间复杂度
- 快排的Java实现:
- 5. Arrays工具类得使用
3. 数组
3.1 数组的概述
数组(Array),多个相同类型数据按一定顺序排列的集合,通过下标对数组元素进行管理
-
数组本身是引用数据类型,而数组中的元素可以是基本数据类型或引用数据类型
-
创建数组对象会在堆中开辟一整块连续的空间,并将这块内存空间的首地址返还给数组名。
-
数组分类:
按照维度分类:一维数组,二维数组,…
按照数据类型分类:基本数据类型元素的数组、引用数据类型元素的数组…
3.2 一维数组的使用
3.2.1 一维数组初始化
数组声明方式:
数据类型 数组名[];或数据类型[] 数组名;
- Java语言中声明数组时不能指定其长度(数组中元素的数), 例如: int a[5]; //非法,C++中允许(C++中声明的同时就在堆区开辟空间了,但Java声明只是在栈区开辟空间)
数组初始化方式:
动态初始化:数组初始化和数组元素赋值分开进行
int[] arr = new int[3]; arr[0] = 3; arr[1] = 9; arr[2] = 8;静态初始化:数组初始化和数组元素赋值同时进行
中括号不能写,等号右边可以直接写大括号的内容
int arr1[] = new int[]{ 3, 9, 8}; int[] arr2 = {3,9,8};静态初始化中括号内不能写数值
//数组变量声明不需要说明数组长度(因为只是在栈区开辟空间)如
int array[];
//但创建数组变量就需要指明数组长度以便在堆区开辟内存空间
int array1[] = new int[10];//指明10个int类型空间
int array2[] = {1,2,3,4};//也指明要开辟4个int内存空间
数组元素的引用方式:
数组元素下标可以是整型常量或整型表达式。如a[3] , b[i] , c[6*i];
每个数组都有一个属性length指明它的长度,用法
int array[]={1,2,3}; System.out.println(array.length);//输出长度
数组一旦创建,数组中元素就会被初始化,按数据元素类型不同有不同的初始化方式
- 对于基本数据类型而言,默认初始化值各有不同(看下表)
- 对于引用数据类型而言,默认初始化值为null(注意与0不同!)
下面时数组元素的默认初始化值:
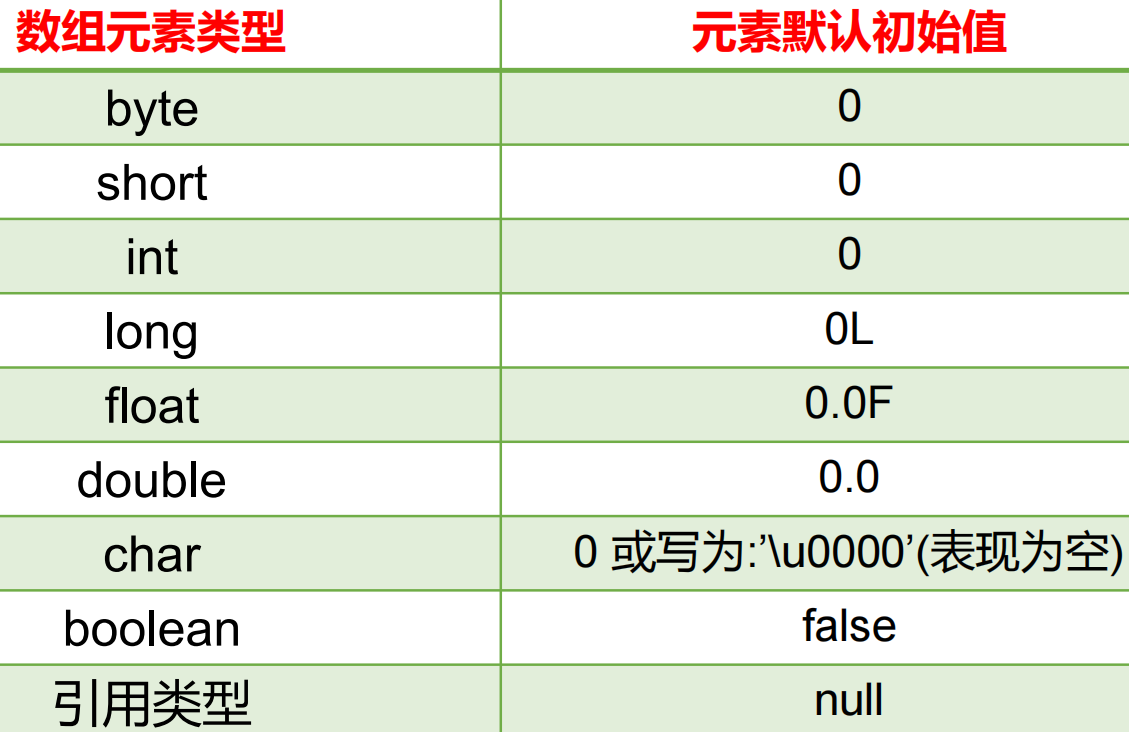
值得一提的是char的初始值对应的ASCll码值是0,也就是null,但在输出的时候会输出个空格,而空格的ASCll码值是32。引用数据类型如String,该数组输出就是null。

3.2.2 一维数组内存解析
常用内存种类和作用

数组静态声明,动态声明,基本数据类型数组,引用数据类型数组,new开辟空间的内存解析。

arr在栈区,存的是数组在堆区开辟的空间的首地址。而new出的数组空间存在堆区,并将首地址值赋给arr,在这里堆区的4个int的初始值是0;
String类型的数组元素初值是null。值得注意的是,并不是将“刘德华”直接赋值,“刘德华”放在字符常量池
3.3 多维数组的使用
多维数组就是数据元素为低维数组,二维数组的数组元素是一维数组,可以理解为一棵树的结构。
二维数组,可以看成是一维数组array1又作为另一个一维数组array2的元素而存在。其实,从数组底层的运行机制来看,其实没有多维数组,都是通过地址来实现高维数组。
3.3.1 多维数组初始化
这里以二维数组为例

3.3.2 多维数组的注意事项:
-
动态初始化的两种方式区别就在于第二层数组是否有分配空间,并且对于两种动态初始化后数组元素有不同的初值。
第一种动态初始化第一层数组元素对应的是第二层数组的首地址
第二种动态初始化第一层元素值为null,不可解引用,具体如下:
//静态初始化 int[][] arr=new int[][] {{1,2,3},{4,5}}; //动态初始化第一种 int[][] arr2=new int[2][2]; System.out.println(arr2[0][0]);//输出0 System.out.println(arr2[0]);//[I@626b2d4a输出的是数组元素的首地址 //动态初始化第二种 //不同于C++,C++不允许这样的写法,C++必须写明实际所需的空间的大小! int[][] arr1=new int[2][]; System.out.println(arr1[0]);//输出null System.out.println(arr1[0][0]);//错误,null无法解引用 //在堆区实际没给第二层数组分配空间,第一层数组初始值为null //java.lang.NullPointerException:Cannot load from int array because "arr1[0]" is null空指针 -
二维数组其他写法
//括号位置摆放自由 int[][] arr4=new int[][] {{1,2,3},{4,5}};//正确 int arr5[][]=new int[][] {{1,2,3},{4,5}};//正确 int[] arr6[]=new int[][] {{1,2,3},{4,5}};//正确 //类型自动推断,将赋值的内容按照前面个数组声明的类型转换,转不了就报错,如下: int[] arr8= {1,2,3};//正确 int[] arr7[]={{1,2,3},{4,5}};//正确 int[] arr8[]={{1.2,2,3},{4,5}};//错误,Type mismatch: cannot convert from double to int //赋值类型要要匹配,不匹配滿足類型提升也行 double[] arr9 = new double[] {1,2};//正确满足类型提升 int[] arr10[]={{1.2,2,3},{4,5}};//错误,Type mismatch: cannot convert from double to int //如果写new,那么数组声明类型和new的类型一定要一致! double[] arr11 = new int[2];// 错误,声明是double类型数组,但堆区开辟空间开的是int类型,显然不合理。可以是开辟double的空间,将int赋值进去,这时合理的,如下 double[] arr12 = {1,2};//正确 doubele[] arr13 = new double[]{1,2};//正确 //int[] arr8; //arr8= {1,2,3}; //分开写错误 -
二维数组动态初始化第二种
int[][] arr = new int[3][];,由于数组元素是数组,所以对注意数组元素的赋值方式。此外二维数组第一种动态初始化是内层数组长度一样,二维数组第二种动态初始化是内层数组不一样。 -
对于一维数组,length就是表示长度。但对于二维数组如:**
int[][] arr = new int[][]{{3,8,2},{2,7},{9,0,1,6}};**length就和堆区开辟的空间关系有关系了,arr.length表示arr直接对应的数组的长度(该数组元素为数组),也就是三。如果想查看第二层数组的长度可以arr[0].lenght等等。
3.3.3 int[] x,y[]
x是int型的一维数组,y是int型的二维数组!int[]是一个整体,x是一个整体,y[]是一个整体。
-
x=y 是否合法?
不合法!虽然都是地址的值但是地址类型有区别
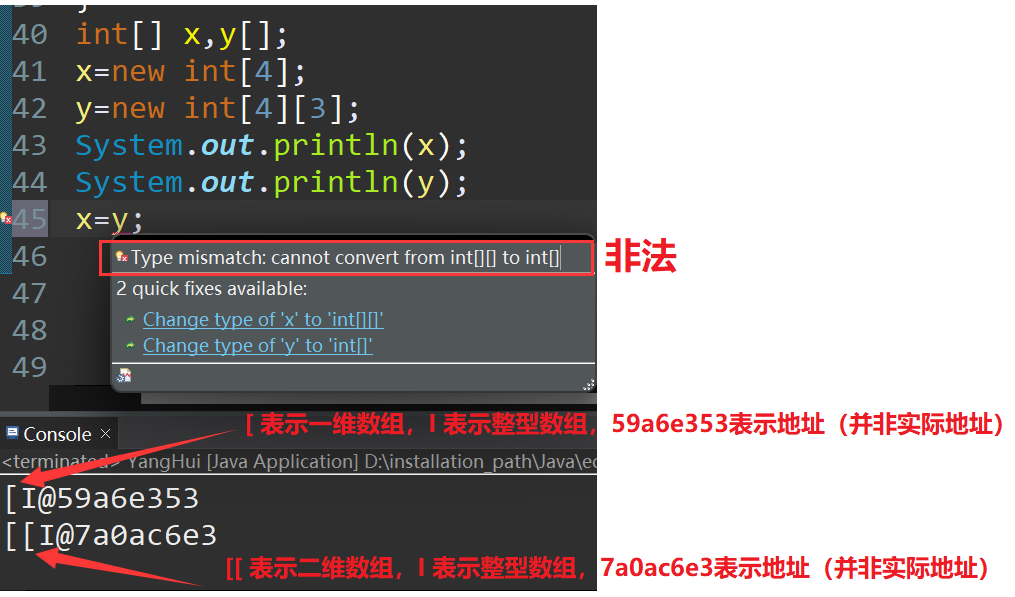
注意数组名之际存的是地址值,在做数组复制的时候不要想当然的直接对数组名进行赋值,而是循环遍历赋值。
3.3.4 多维数组的内存解析

3.4 数组中涉及到的常见算法
3.4.1 线性查找
就遍历,略
3.4.2 二分法查找算法
思路总结:对于有序的数组,定义头和尾两个标识,通过比对数组中间的元素和目标元素,每次缩小一半的搜索范围,达到快速检索的目的。实现内部使用三个if语句分类判断。

- 前提,二分法查找数组元素的前提是一个有序数组!
//二分法查找:要求此数组必须是有序的。
int[] arr3 = new int[]{-99,-54,-2,0,2,33,43,256,999};
boolean isFlag = true;
int number = 256;
//int number = 25;
int head = 0;//首索引位置
int end = arr3.length - 1;//尾索引位置
while(head <= end)
{
int middle = (head + end) / 2;
if(arr3[middle] == number)
{
System.out.println("找到指定的元素,索引为:" + middle);
isFlag = false;
break;
}
else if(arr3[middle] > number)
{
end = middle - 1;
}
else
{
//arr3[middle] < number
head = middle + 1;
}
}
if(isFlag)
{
System.out.println("未找打指定的元素");
}
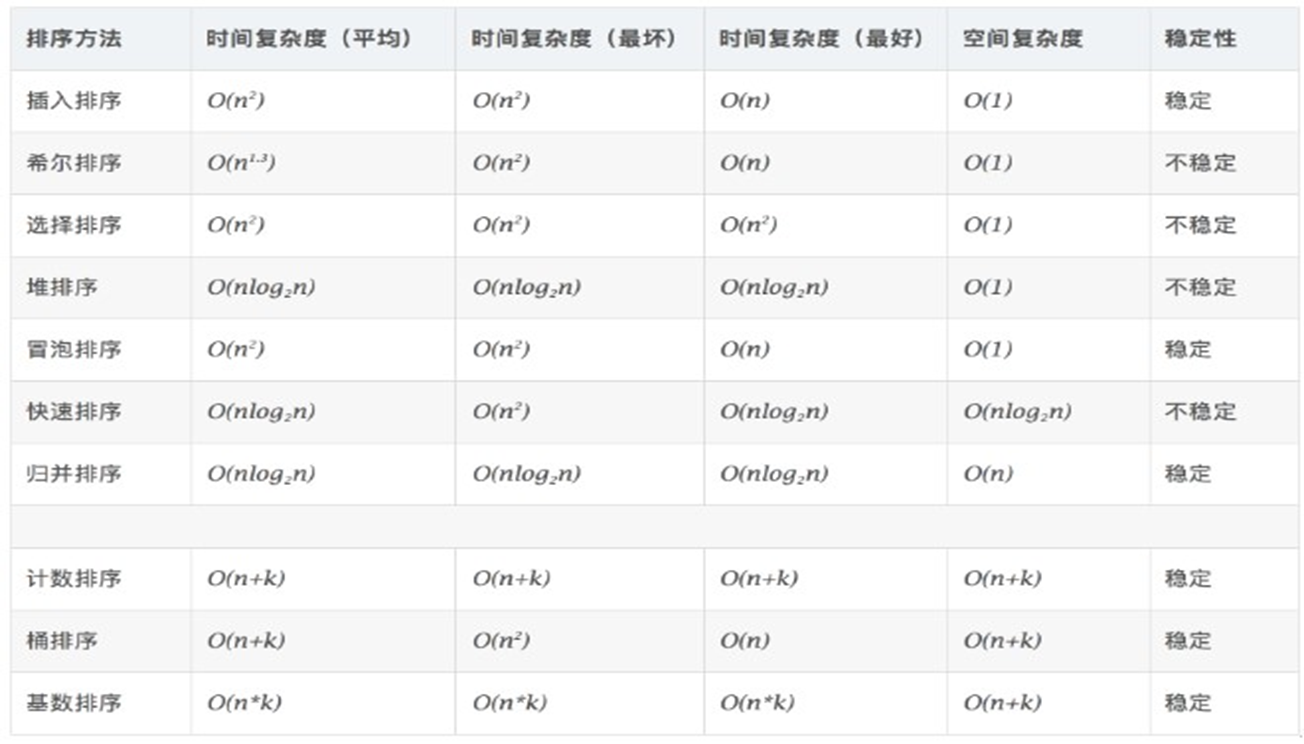
3.4.3 排序算法
通常来说,排序的目的是快速查找。
衡量排序算法的优劣:
时间复杂度:分析关键字的比较次数和记录的移动次数
空间复杂度:分析排序算法中需要多少辅助内存
稳定性:若两个记录A和B的关键字值相等,但排序后A、B的先后次序保
持不变,则称这种排序算法是稳定的。
- 根据是否需要外部存储器,排序算法又分为内部排序和外部排序
排序算法分类:内部排序和外部排序。
内部排序:整个排序过程不需要借助于外部存储器(如磁盘等),所有排序操作都在内存中完成。
外部排序:参与排序的数据非常多,数据量非常大,计算机无法把整个排序过程放在内存中完成,必须借助于外部存储器(如磁盘)。外部排序最常见的是多路归并排序。可以认为外部排序是由多次内部排序组成。
3.4.3.1 十大内部排序算法
- 选择排序
- 堆排序

- 冒泡排序
- 快速排序
- 直接插入排序
- 折半插入排序
- Shell排序
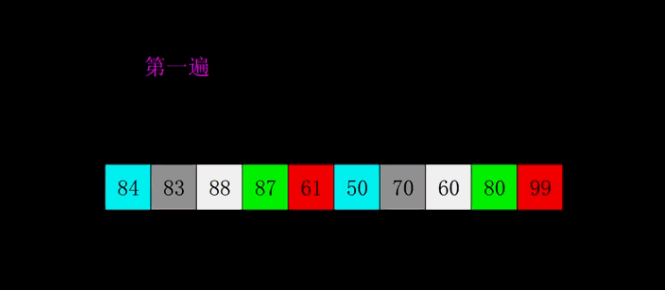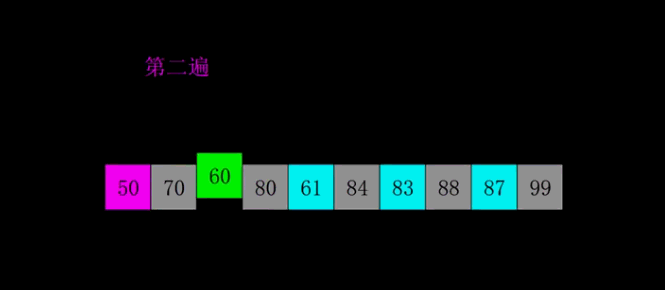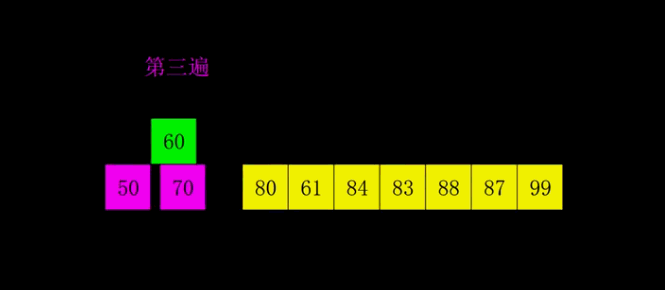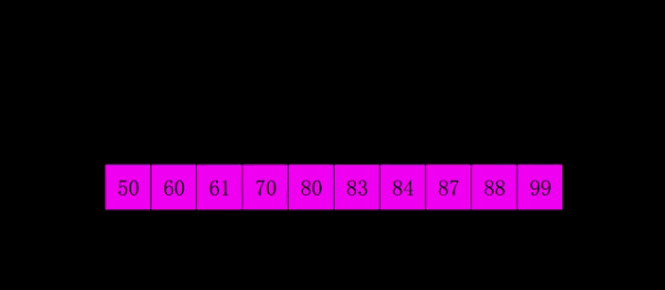
- 归并排序

- 桶式排序
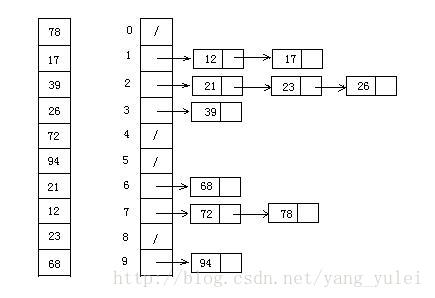
- 基数排序

此外计数排序: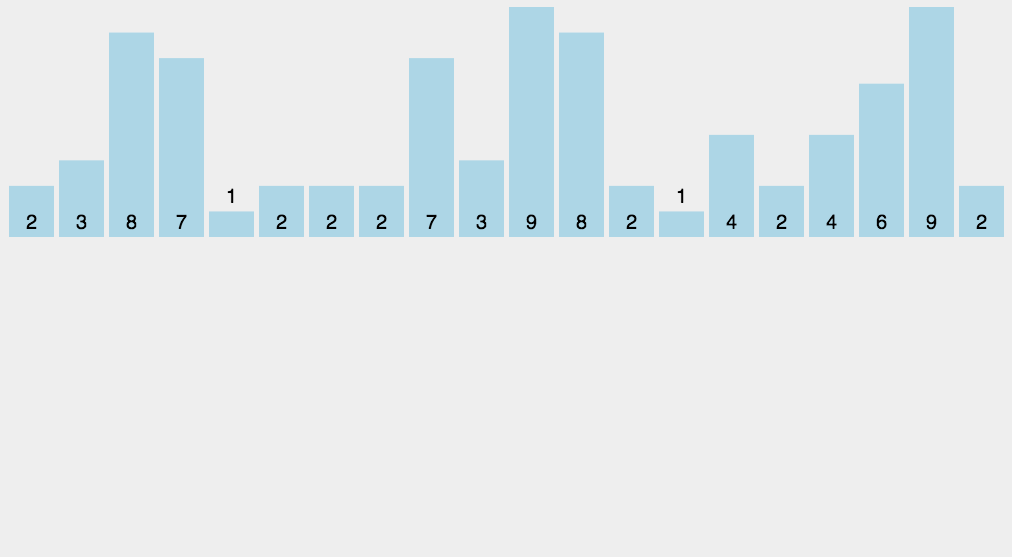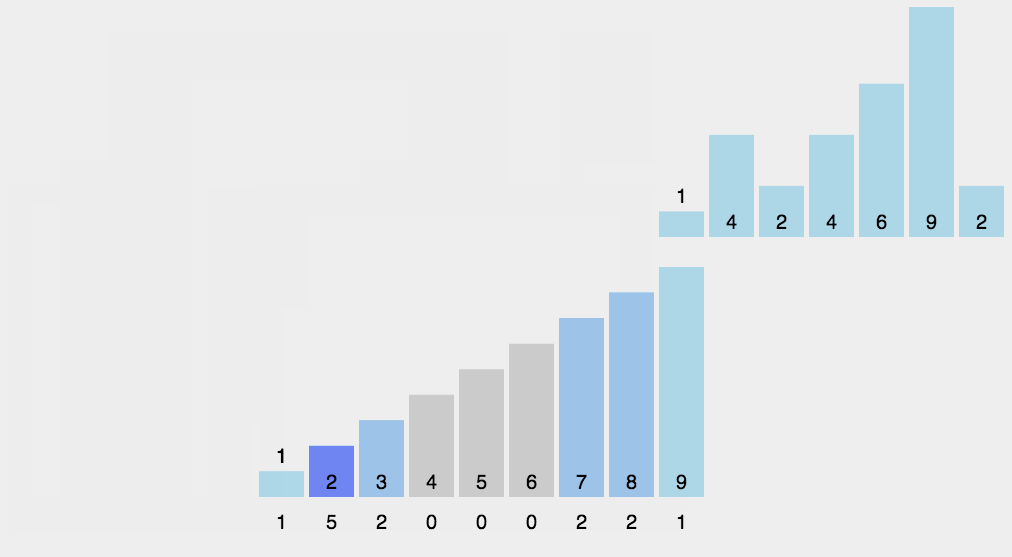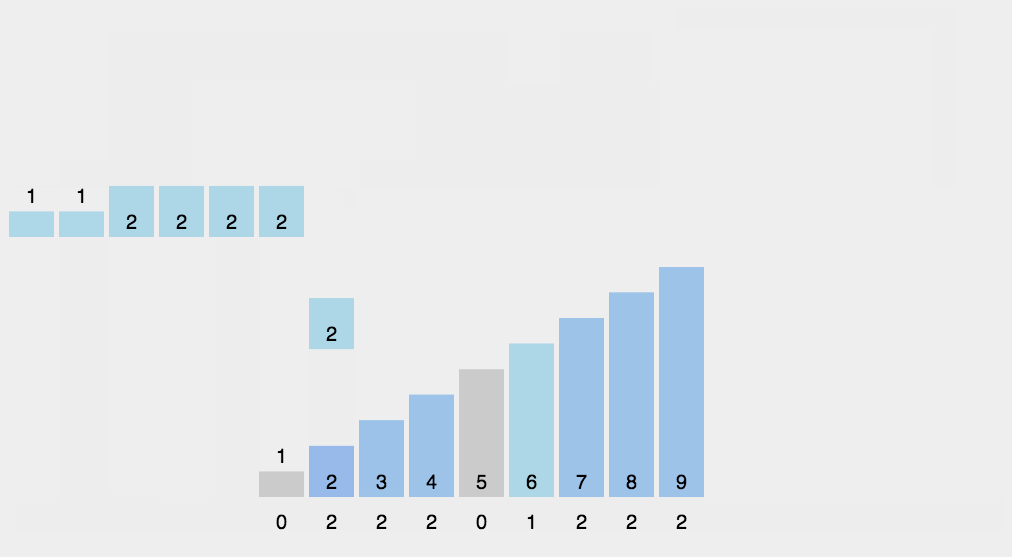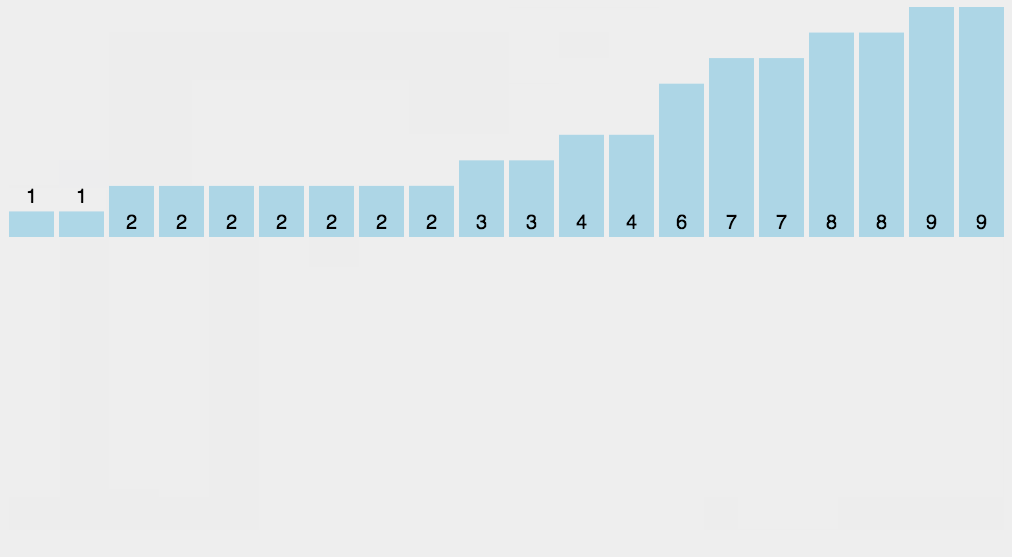
3.4.2 算法特点概述
3.4.4 快速排序
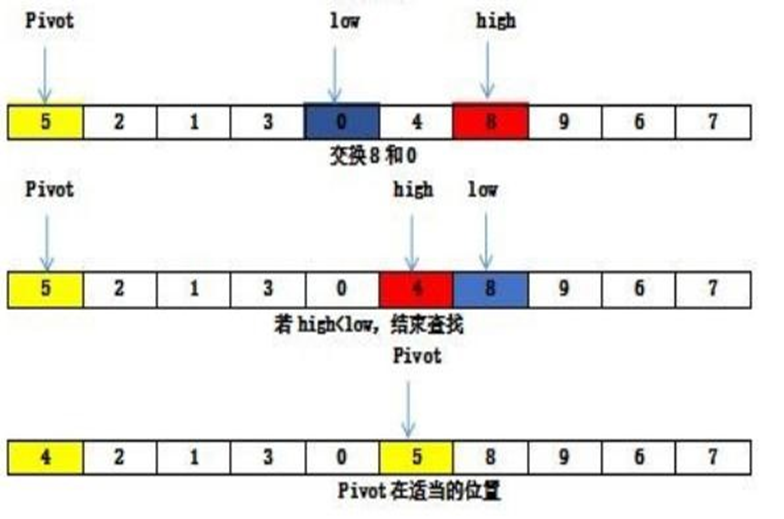
快排思想
从数列中挑出一个元素,称为"基准"(pivot),
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就就将原来的数组分为了两个部分,注意:基准不一定再正中间!这个称为分区(partition)操作。
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,都会确定一个元素的位置。

快排的时间复杂度
对于长度为n的数组,快排循环一次,确定一个元素的位置。并将数组分为长度分别为I1和I2的子数组。
T(n)表示长度为n的数组快排所需的时间复杂度,D(n)=n-1是一趟快排需要的比较次数,一趟快排结束后将数组分成两部分 I1 和 I2。由递归出以下三种时间复杂度:
1.最好时间复杂度:
- 就是快排每次划分将数组划分成两个等长子数组
I1=I2
设 n 为待排序数组中的元素个数, T(n) 为算法需要的时间复杂度,递归得:
T ( n ) = { D ( 1 ) , n ≤ 1 D ( n ) + T ( I 1 ) + T ( I 2 ) , n > 1 T(n)= \begin{cases} D(1),&n\leq1\\ D(n)+T(I1)+T(I2),&n>1 \end{cases} T(n)={D(1),D(n)+T(I1)+T(I2),n≤1n>1
所以
T ( n ) = D ( n ) + T ( I 1 ) + T ( I 2 ) = D ( n ) + D ( n 2 ) + D ( n 2 ) + . . . . = n − 1 + 2 ( n 2 − 1 ) + 2 2 ( n 2 2 − 1 ) + . . . + 2 k ( n 2 k − 1 ) = n − 1 + n − 2 + n − 2 2 + . . . n − 2 k ∵ n = 2 k ∴ k = l o g 2 n ∴ T ( n ) = l o g 2 n − 2 n + 1 \begin{aligned} T(n)&=D(n)+T(I1)+T(I2)\\ &=D(n)+D(\frac{n}{2})+D(\frac{n}{2})+....\\ &=n-1+2(\frac{n}{2}-1)+2^2(\frac{n}{2^2}-1)+...+2^k(\frac{n}{2^k}-1)\\ &=n-1+n-2+n-2^2+...n-2^k\\ &\because n=2^k\\ &\therefore k=log_2^n\\ &\therefore T(n)=log_2^n-2n+1 \end{aligned} T(n)=D(n)+T(I1)+T(I2)=D(n)+D(2n)+D(2n)+....=n−1+2(2n−1)+22(22n−1)+...+2k(2kn−1)=n−1+n−2+n−22+...n−2k∵n=2k∴k=log2n∴T(n)=log2n−2n+1
- 第二种理解:循环一次将数组分为两个子数组,快排结束的条件是所有子数组的元素个数为1。所以确定数组n个元素的位置,每次循环子数组个数为1,2,22…2k=n,每次循环的时间复杂度乘以子数组隔宿即可,也就是
T ( n ) = 1 ( n − 1 ) + 2 ( n 2 − 1 ) + 2 2 ( n 2 2 − 1 ) + . . . + 2 k ( n 2 k − 1 ) = n − 1 + n − 2 + n − 2 2 + . . . n − 2 k ∵ n = 2 k ∴ k = l o g 2 n ∴ T ( n ) = l o g 2 n − 2 n + 1 \begin{aligned} T(n)&=1(n-1)+2(\frac{n}{2}-1)+2^2(\frac{n}{2^2}-1)+...+2^k(\frac{n}{2^k}-1)\\ &=n-1+n-2+n-2^2+...n-2^k\\ &\because n=2^k\\ &\therefore k=log_2^n\\ &\therefore T(n)=log_2^n-2n+1 \end{aligned} T(n)=1(n−1)+2(2n−1)+22(22n−1)+...+2k(2kn−1)=n−1+n−2+n−22+...n−2k∵n=2k∴k=log2n∴T(n)=log2n−2n+1
2.最坏时间复杂度
-
就是快排每次划分将数组划分成的两个子数组长度为
I1=0,I2=n-1设 n 为待排序数组中的元素个数, T(n) 为算法需要的时间复杂度,递归得:
T ( n ) = { D ( 1 ) , n ≤ 1 D ( n ) + T ( 0 ) + T ( n − 1 ) , n > 1 T(n)= \begin{cases} D(1),&n\leq1\\ D(n)+T(0)+T(n-1),&n>1 \end{cases} T(n)={D(1),D(n)+T(0)+T(n−1),n≤1n>1
所以
T ( n ) = D ( n ) + T ( n − 1 ) = D ( n ) + D ( n − 1 ) + T ( n − 2 ) = ( n − 1 ) + ( n − 2 ) + ( n − 3 ) + . . . . + ( n − ( n − 1 ) ) = ( n − 1 ) + ( n − 2 ) + . . . + 0 = n ( n − 1 ) 2 = O ( n 2 ) \begin{aligned} T(n)&=D(n)+T(n-1)\\ &=D(n)+D(n-1)+T(n-2)\\ &=(n-1)+(n-2)+(n-3)+....+(n-(n-1))\\ &=(n-1)+(n-2)+...+0\\ &=\frac{n(n-1)}{2}\\ &=O(n^2) \end{aligned} T(n)=D(n)+T(n−1)=D(n)+D(n−1)+T(n−2)=(n−1)+(n−2)+(n−3)+....+(n−(n−1))=(n−1)+(n−2)+...+0=2n(n−1)=O(n2) -
第二中理解:最坏时间复杂度其实就是已经排好了的数组,再次快排,子数组长度为(n-1),(n-2),…,0,时间复杂度就是本身遍历的长度,相加即为快排时间复杂度:
T ( n ) = ( n − 1 ) + ( n − 2 ) + ( n − 3 ) + . . . . + ( n − ( n − 1 ) ) = ( n − 1 ) + ( n − 2 ) + . . . + 0 = n ( n − 1 ) 2 = O ( n 2 ) \begin{aligned} T(n)&=(n-1)+(n-2)+(n-3)+....+(n-(n-1))\\ &=(n-1)+(n-2)+...+0\\ &=\frac{n(n-1)}{2}\\ &=O(n^2) \end{aligned} T(n)=(n−1)+(n−2)+(n−3)+....+(n−(n−1))=(n−1)+(n−2)+...+0=2n(n−1)=O(n2)
3.平均时间复杂度
-
就是每次划分将数组划分成的两个子数组的长度不确定,都是等可能,求时间复杂度就是算个平均值如下:
{ I 1 = 0 , I 2 = n − 1 I 1 = 1 , I 2 = n − 2 . . . . I 1 = n − 1 , I 2 = 0 \begin{cases} &I1=0,I2=n-1\\ &I1=1,I2=n-2\\ &....\\ &I1=n-1,I2=0\\ \end{cases} ⎩ ⎨ ⎧I1=0,I2=n−1I1=1,I2=n−2....I1=n−1,I2=0
所以求解如下,思路就是求平均:
T ( n ) = D ( n ) + 1 n ∑ i = 0 n − 1 [ T ( i ) + T ( n − 1 − i ) ] = D ( n ) + 2 n ∑ i = 0 n − 1 T ( i ) . . . ( 1 ) 式 ∴ T ( n − 1 ) = D ( n − 1 ) + 2 n ∑ i = 0 n − 2 T ( i ) . . . ( 2 ) 式 ∴ n ∗ ( 1 ) − ( n − 1 ) ∗ ( 2 ) 得 : n T ( n ) − ( n − 1 ) T ( n − 1 ) = n D ( n ) + 2 ∑ i = 0 n − 1 T ( i ) − ( n − 1 ) D ( n − 1 ) − 2 ∑ i = 0 n − 2 T ( i ) 整理得 : T ( n ) n + 1 = T ( n − 1 ) n + 2 ( n − 1 ) n ( n − 1 ) 令 B n = T ( n ) n + 1 ,得 \begin{aligned} T(n)&=D(n)+\frac{1}{n}\sum_{i=0}^{n-1}{[T(i)+T(n-1-i)]}\\ &=D(n)+\frac{2}{n}\sum_{i=0}^{n-1}{T(i)}...(1)式\\ &\therefore T(n-1)=D(n-1)+\frac{2}{n}\sum_{i=0}^{n-2}{T(i)}...(2)式\\ &\therefore n*(1)-(n-1)*(2)得:\\ &nT(n)-(n-1)T(n-1)=nD(n)+2\sum_{i=0}^{n-1}{T(i)}-(n-1)D(n-1)-2\sum_{i=0}^{n-2}{T(i)}\\ &整理得:\frac{T(n)}{n+1}=\frac{T(n-1)}{n}+\frac{2(n-1)}{n(n-1)}\\ &令B_n=\frac{T(n)}{n+1},得\\ \end{aligned} T(n)=D(n)+n1i=0∑n−1[T(i)+T(n−1−i)]=D(n)+n2i=0∑n−1T(i)...(1)式∴T(n−1)=D(n−1)+n2i=0∑n−2T(i)...(2)式∴n∗(1)−(n−1)∗(2)得:nT(n)−(n−1)T(n−1)=nD(n)+2i=0∑n−1T(i)−(n−1)D(n−1)−2i=0∑n−2T(i)整理得:n+1T(n)=nT(n−1)+n(n−1)2(n−1)令Bn=n+1T(n),得
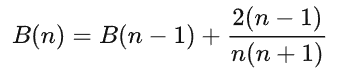
然后求B(n)反代求出T(n),求解过程很复杂不在此描述,最终时间复杂度为
O ( n l o g 2 n ) O(nlog~2^n) O(nlog 2n)
综上:快速排序最好时间复杂度为 O(nlog2n) ,最坏时间复杂度为 O(n2) ,平均时间复杂度为 O(nlog2n)
快速排序的一些改进方案:
-
将快速排序的递归执行改为非递归执行
-
当问题规模 n 较小时 (n≤16) ,采用直接插入排序求解
-
每次选取 prior 前将数组打乱
-
每次选取
E [ f i r s t ] + E [ L a s t ] 2 \frac{E[first]+E[Last]}{2} 2E[first]+E[Last]
或
E [ f i r s t ] + E [ l a s t ] + E [ ( f i r s t + l a s t ) / 2 ] 3 \frac{E[first]+E[last]+E[(first+last)/2]}{3} 3E[first]+E[last]+E[(first+last)/2]
作为 prior
快排的Java实现:
/**
* 快速排序
* 通过一趟排序将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分关键字小,
* 则分别对这两部分继续进行排序,直到整个序列有序。
* @author Answer
* 2022.8.11
*/
public class QuickSort
{
//交换数据函数包装
private static void swap(int[] data, int i, int j)
{
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
//函数主体
private static void subSort(int[] data, int start, int end)
{
if (start < end)
{
int base = data[start];
int low = start;
int high = end + 1;
while (true)
{
while (low < end && data[++low] - base <= 0);//low < end,是用于迭代时防止超出范围的限制
while (high > start && data[--high] - base >= 0);
if (low < high)
{
swap(data, low, high);
}
else
{
break;
}
}
swap(data, start, high);
subSort(data, start, high - 1);//递归调用
subSort(data, high + 1, end);
}
}
public static void quickSort(int[] data)
{
subSort(data,0,data.length-1);
}
public static void main(String[] args)
{
int[] data = { 9, -16, 30, 23, -30, -49, 25, 21, 30 };
System.out.println("排序之前:\n" + java.util.Arrays.toString(data));
quickSort(data);
System.out.println("排序之后:\n" + java.util.Arrays.toString(data));
}
}
-
快排分内外层两循环,其中两个内层循环做的是将将当前小于pivot的元素分到一边(结束时是以大于pivot的元素head结束),将当前大于pivot的元素分到另一边(结束时是以小于pivot的元素tail结束),
然后交换head和tail,再次进入外层循环。通过两层循环将大于和小于pivot的元素进行分组,再对子数据进行iteration。
-
high=end+1;这个设定很微妙!大大简化代码量!函数体中要排序的下标范围是1~array.length-1,但设置的头是0,尾部是array.length。这样的设定决定函数在对pivot进行比对的时候,需要先自增自减再比对,当然也可以设定头是1,尾部是array.length-1。这样就需要先比较,再根据判断结果决定是否需要对下标进行移动,因此再内层循环中需添加if语句,代码冗杂。不如第一种精巧的设定 -
迭代注意:再函数题内部用于迭代函数的参数一般不写具体数值,否则无论迭代多少次,参数均不变,与迭代的目的向背。而应该写的是函数内部定义的变量,这样函数执行一次参数都发生变化,才符合我们的预期。
5. Arrays工具类得使用
java.util.Arrays类即为操作数组的工具类,包含了用来操作数组(比如排序和搜索)的各种方法,可以直接调用Arrays类中的方法对数组进行操作
| 1 | boolean equals(int[] a,int[] b) | 判断两个数组是否相等。 |
|---|---|---|
| 2 | String toString(int[] a) | 输出数组信息。 |
| 3 | void fill(int[] a,int val) | 将指定值填充到数组之中 |
| 4 | void sort(int[] a) | 对数组进行排序。 |
| 5 | int binarySearch(int[] a,int key) | 对排序后的数组进行二分法检索指定的值。 |






![[SpringBoot] 多模块统一返回格式带分页信息](https://img-blog.csdnimg.cn/2c616a4ab4f14f8ba67f1385beff5ba2.png)