Scalable Diffusion Models with State Space Backbone
公和众和号:EDPJ(进 Q 交流群:922230617 或加 VX:CV_EDPJ 进 V 交流群)
目录
0. 摘要
2. 方法
2.1 基础
2.2 模型结构设计
3. 实验
0. 摘要
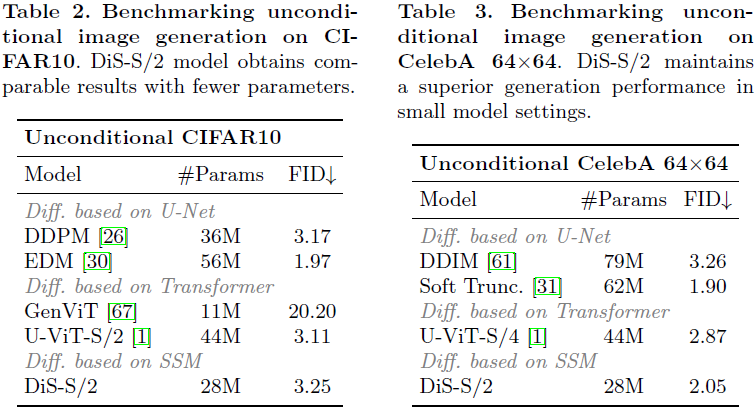
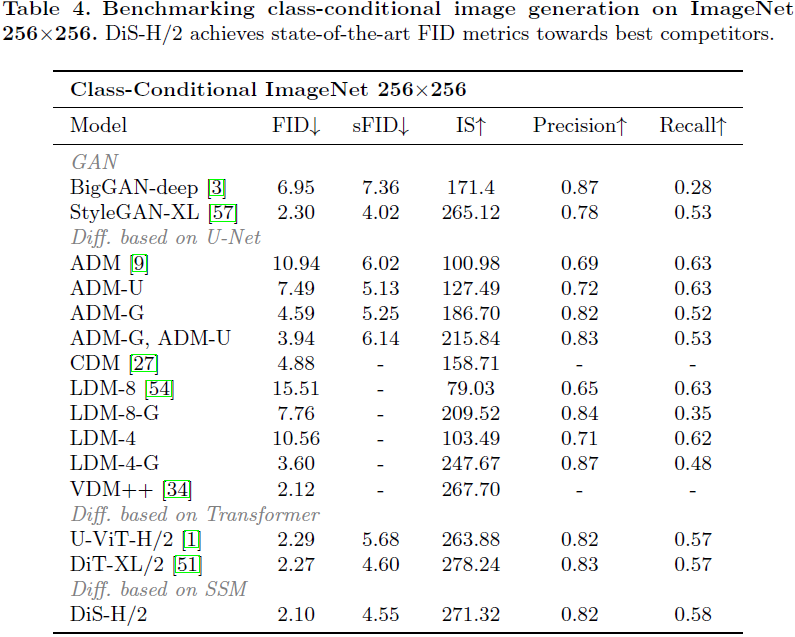
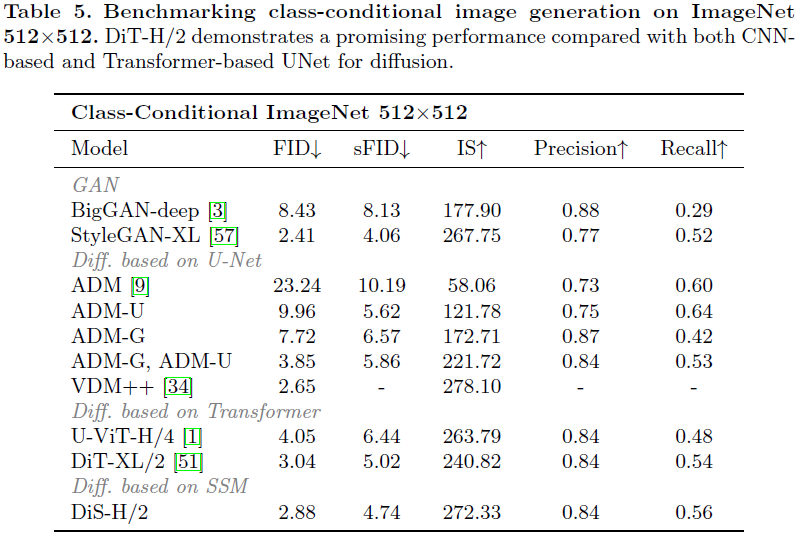
这篇论文提出了一种建立在状态空间架构之上的扩散模型的新探索。我们努力训练用于图像数据的扩散模型,其中传统的 U-Net 骨干被状态空间(state space)骨干替代,该骨干可在原始补丁或潜在空间上运行。由于其在容纳长距离依赖性方面的显著效力,扩散状态空间模型(Diffusion State Space,DiS)通过将所有输入,包括时间、条件和嘈杂的图像补丁,视为标记而得以区分。我们对 DiS 的评估涵盖了无条件和类别条件图像生成场景,揭示了 DiS 在与同等规模的基于 CNN 或 Transformer 的 U-Net 架构相比,表现相当或更为优越。此外,我们分析了 DiS 的可伸缩性,通过在 Gflops 中量化的前向传递复杂性来衡量。通过增加深度/宽度或增加输入标记实现更高Gflops 的 DiS 模型一致显示出更低的 FID。除了展示令人钦佩的可伸缩性特征外,位于潜在空间的 DiS-H/2 模型在 256×256 和 512×512 分辨率下在类条件 ImageNet 基准上达到了与先前扩散模型相当的性能水平,同时显著减轻了计算负担。
代码:https://github.com/feizc/DiS
2. 方法
2.1 基础
扩散。
状态空间骨干。
2.2 模型结构设计
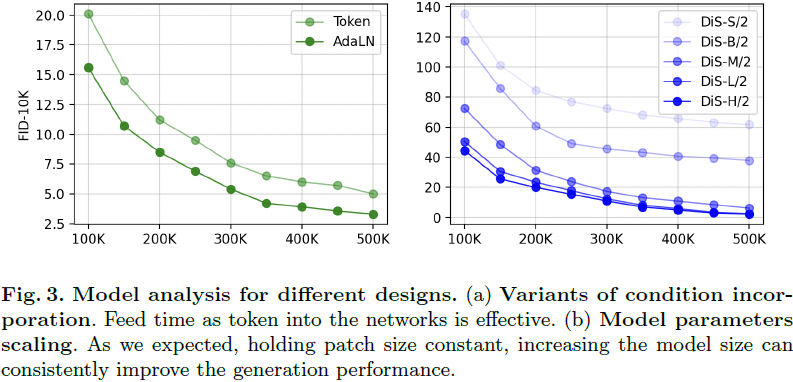
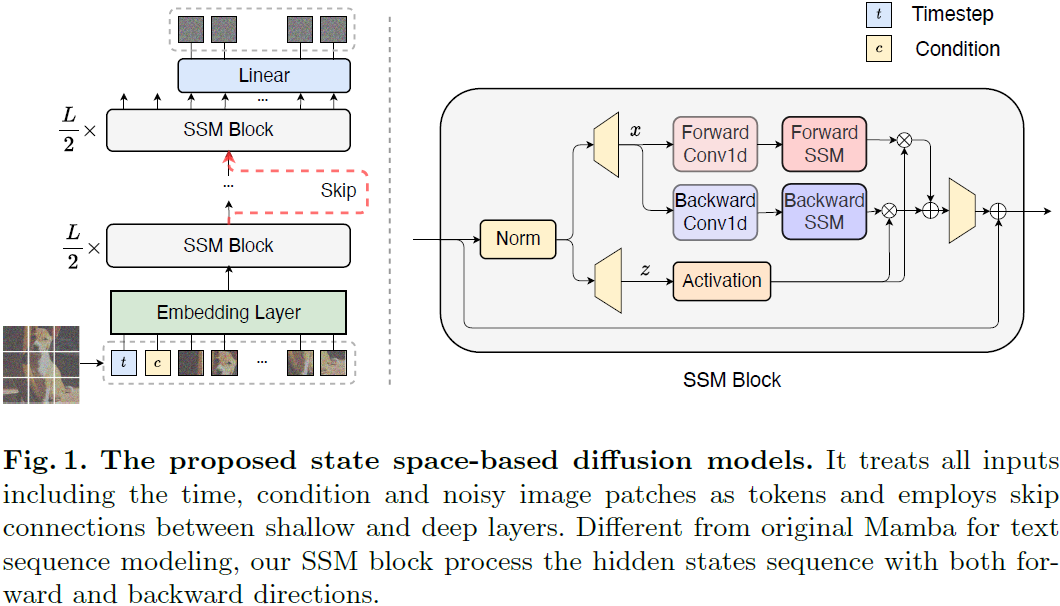
我们引入扩散状态空间模型,简称为 DiS,这是一种用于图像生成中的扩散模型的简单而通用的架构。具体而言,DiS 对噪声预测网络 ϵθ(xt, t, c) 进行参数化,该网络以时间步 t、条件 c 和带噪图像 xt 为输入,并预测注入到 xt 中的噪声。我们的目标是密切遵循先进的状态空间架构以保持其可伸缩性特征,因此 DiS 基于双向 Mamba [16,72] 架构,该架构对标记序列进行操作。图 1 提供了完整 DiS 架构的概述。在本节中,我们详细说明了 DiS 的前向传递,以及 DiS 类别的设计空间的组件。
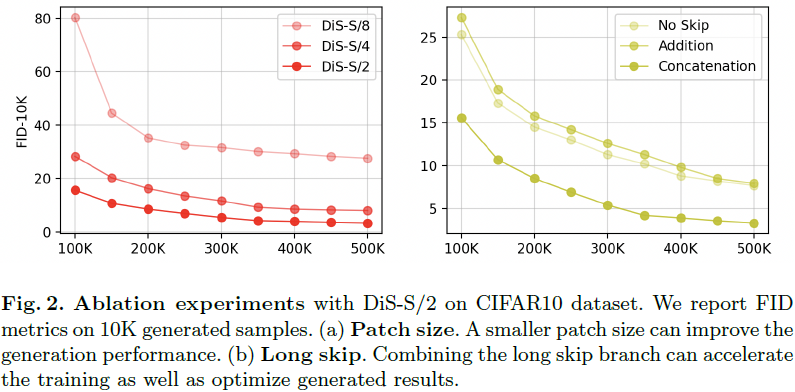
图像 patch 化(patchnify)。DiS 的第一层对输入图像 I ∈ R^(H×W×C) 进行变换,将其转换为展平的 2D patch X ∈ R^(J×(p^2·C))。随后,通过线性嵌入输入中的每个 patch,将其转换为维度为 D 的 J 个标记的序列。与 [11] 一致,我们对所有输入标记应用可学习的位置嵌入。由 patchnify 创建的标记数 J 由超参数 patch 大小 p 决定,为 H×W / p^2。patchnify 支持原始像素和潜在空间。我们将 p 设置为 2、4、8。
SSM 块。在嵌入层之后,输入标记经过一系列 SSM 块的处理。除了带噪声的图像输入,扩散模型有时会处理额外的条件信息,如噪声时间步 t、条件 c(如类别标签或自然语言)。鉴于原始的Mamba 块是为 1-D 序列设计的,我们求助于 [72],该论文融入了针对视觉任务的双向序列建模。这些设计对标准 SSM 块设计引入了微妙但关键的修改。如图 1 的右侧所示,SSM 块的前向传递结合了正向和反向方向。
跳跃连接。给定一系列 L 个 SSM 块,我们将堆叠的 SSM 块分为前半部分 ⌊L/2⌋ 浅层组、一个中间层和后半部分 ⌊L/2 ⌋ 深层组。令 h_shallow、h_deep ∈ R^(J×D) 分别为主分支和长跳跃分支的隐藏状态。我们考虑直接将它们连接并进行线性投影,即 Linear(Concat(h_shallow, h_deep)),然后将它们馈送到下一个 SSM 块之前。
线性解码器。在最终的 SSM 块之后,我们需要将隐藏状态序列解码为输出噪声预测和对角协方差预测。这两个输出保留与原始空间输入相同的形状。我们使用标准的线性解码器,即应用最终层的归一化和线性解码每个标记为 p^2 ·C 张量。最后,我们重新排列解码后的标记以获得预测的噪声和协方差。
条件整合。为了有效地整合额外的条件,我们采用了一种简单的策略,即将时间步 t 和条件 c 的向量嵌入作为输入序列中的两个补充标记追加。这些标记被等同对待于图像标记,类似于 Vision Transformers [11] 中的 cls 标记的方法。这种方法使得可以利用 SSM 块而无需进行任何修改。在最终块之后,将条件标记从序列中移除。我们还探索了自适应归一化层,其中将标准归一化层替换为自适应归一化层。也就是说,我们不是直接学习维度方向的比例和偏移参数,而是从 t 和 c 的嵌入向量的和中回归它们,这将在实验部分讨论。
3. 实验