算法学习——LeetCode力扣贪心篇4

在这里插入图片描述

763. 划分字母区间

763. 划分字母区间 - 力扣（LeetCode）

描述

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

示例

示例 1：
输入：s = “ababcbacadefegdehijhklij”
输出：[9,7,8]
解释：
划分结果为 “ababcbaca”、“defegde”、“hijhklij” 。
每个字母最多出现在一个片段中。
像 “ababcbacadefegde”, “hijhklij” 这样的划分是错误的，因为划分的片段数较少。

示例 2：

输入：s = “eccbbbbdec”
输出：[10]

提示

1 <= s.length <= 500
s 仅由小写英文字母组成

代码解析

题意简述为
即最多能切多少段？使得同一字母都出现在一个片段，且片段最多。

思路
先统计整个字符串的map字典。
然后再次遍历字符串，当遍历字符串某一点时，当前字符串区间出现的字母个数就是整个字符串的字母个数（即当前字符串区间出现的字母，全部都出现在这里，区间外没有这个字母再次出现了），纪录当前区间是一段。

class Solution {
public:
    vector<int> partitionLabels(string s) {
        
        map<char,int> my_map; //整个字符串字典
        map<char,int> my_map_tmp;// 一段的字典
        vector<int> result;
        int start = 0; //段开始标志
        for(int i=0 ; i< s.size() ; i++) my_map[s[i]]++;

        // for(auto it:my_map) cout<<it.first<<' '<<it.second<<endl;

        for(int i=0 ; i<s.size() ;i++)
        {
            my_map_tmp[s[i]]++; //更新一段的字典
            //检查当前的字典和全局字典，字母出现的次数
            for(auto it = my_map_tmp.begin() ; it != my_map_tmp.end() ;it++)
            {
            	//当前段中字母出现个数和全局不同（即还有字母没发现），跳出
                if( it->second != my_map[it->first]) break;
                //当前段出现的字母，字母数量和全局数量都相同（即全发现）
                if(it == -- my_map_tmp.end() ) //遍历到最后一个字母都没跳出
                {
                    result.push_back(i-start+1); //记录段长度
                    start = i+1; //下一段开始点
                    my_map_tmp.clear();//清空段字典
                }
            }
        }
        
        return result;
    }
};

56. 合并区间

56. 合并区间 - 力扣（LeetCode）

描述

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

示例

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

提示

1 <= intervals.length <= 104
intervals[i].length == 2
0 <= starti <= endi <= 104

代码解析

按照左边界排序，排序之后局部最优：每次合并都取最大的右边界，这样就可以合并更多的区间了，整体最优：合并所有重叠的区间。

其实就是用合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

class Solution {
public:
    static bool compare(vector<int>&a , vector<int>&b)
    {
        return a[0] < b[0];
    }
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        
        if(intervals.size() <= 1) return intervals;
        vector<vector<int>> result;
        //按照区间左边界排序
        sort(intervals.begin() , intervals.end(),compare);
        //第一个区间作为临时区间
        vector<int> tmp = intervals[0];

        for(int i = 1 ; i< intervals.size() ; i++)
        {
        	//如果当前区间和临时区间有重叠
        	//取临时区间和当前区间的公共集合作为新的临时区间
            if(tmp[1] >= intervals[i][0])
            {
                tmp[0] = min(tmp[0] , intervals[i][0]);
                tmp[1] = max(tmp[1] , intervals[i][1]);
            }
            else//当临时区间和当前区间不重合
            {
                result.push_back(tmp);//临时区间存入
                tmp = intervals[i];//当前区间为新的临时区间
            }
            if(i==intervals.size()-1)//当前区间是最后一个区间的时候
            {
                 result.push_back(tmp);//存入未存入的临时区间
            }
        }
        return result;
    }
};

738. 单调递增的数字

738. 单调递增的数字 - 力扣（LeetCode）

描述

当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。

给定一个整数 n ，返回小于或等于 n 的最大数字，且数字呈单调递增。

示例

示例 1:

输入: n = 10
输出: 9

示例 2:

输入: n = 1234
输出: 1234

示例 3:

输入: n = 332
输出: 299

提示

0 <= n <= 109

代码解析

找到一个比目标值小的最大递增数列

递归法

从左到右遍历，找符合递增的部分，
当发现不符合的部分，不符合部分都置9
找到符合部分-1的最大递增数（后面都置9要借位）

例：输入668841
发现6688部分符合递增，但是从4开始不符合，因此41变成99
之后找到6688-1的最大递增（后面99要借1）为6679
在和最后两个99合并，得到667999

class Solution {
public:
    int monotoneIncreasingDigits(int n) {
        
        if(n<10) return n;
        string num = to_string(n);
        string result ;
        result += num[0];
        int flag = 0; //是否符合标志位，当不符合递增的时候，后面都置9
        for(int i=1 ;i<num.size();i++) //遍历
        {
            if(num[i] >= num[i-1] && flag==0) //找到符合递增的部分
            {
                result += num[i];
            }
            else if(flag==0) //找到第一个不符合递增的数 ，并求之前符合部分-1最大递增
            {
                result = to_string(monotoneIncreasingDigits(stoi(result)-1) );
                flag = 1; //设置为不符合
            }

            if(flag == 1) //不符合后面全都置9
            {
                 result += '9';
            }
        }

        return stoi(result);
    }
};

贪心法反向遍历

局部最优：遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]–，然后strNum[i]给为9，可以保证这两位变成最大单调递增整数。

全局最优：得到小于等于N的最大单调递增的整数。

但这里局部最优推出全局最优，还需要其他条件，即遍历顺序，和标记从哪一位开始统一改成9。

那么从后向前遍历，就可以重复利用上次比较得出的结果了，从后向前遍历332的数值变化为：332 -> 329 -> 299

class Solution {
public:
    int monotoneIncreasingDigits(int n) {
        
        if(n<10) return n;
        string num = to_string(n);
        int flag;
      
        for(int i=num.size()-1 ; i >=1 ;i--)
        {
           if(num[i] < num[i-1])
           {
               flag = i;
               num[i-1] -= 1;
           }
        }

        for(int i = flag ; i<num.size() ;i++)
        {
            num[i] = '9';
        }

        return stoi(num);
    }
};

968. 监控二叉树

968. 监控二叉树 - 力扣（LeetCode）

描述

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例

示例 1：

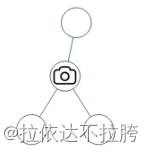
在这里插入图片描述

输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

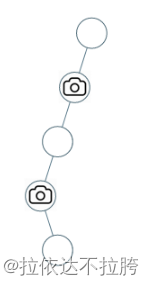
在这里插入图片描述

输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。上图显示了摄像头放置的有效位置之一。

提示

给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。

代码解析

从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！
此时，大体思路就是从低到上，先给叶子节点父节点放个摄像头，然后隔两个节点放一个摄像头，直至到二叉树头结点。

我们分别有三个数字来表示：

0：该节点无覆盖
1：本节点有摄像头
2：本节点有覆盖

情况1：左右节点都有覆盖
左孩子有覆盖，右孩子有覆盖，那么此时中间节点应该就是无覆盖的状态了。
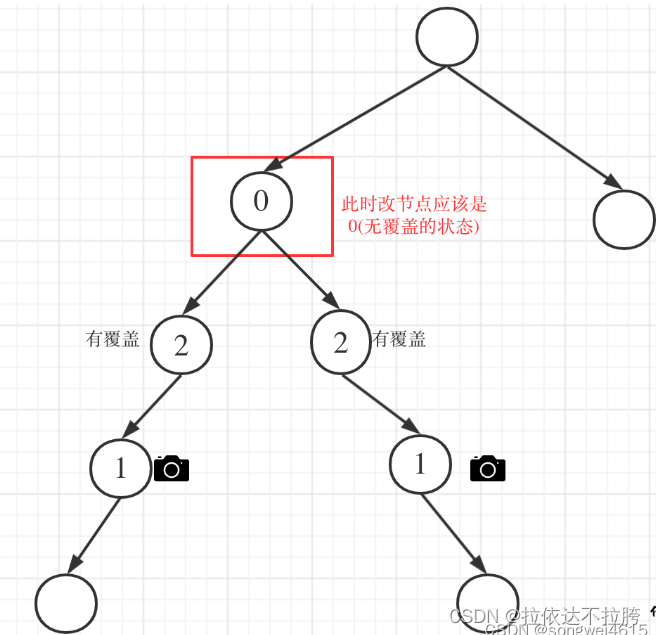
情况2：左右节点至少有一个无覆盖的情况
如果是以下情况，则中间节点（父节点）应该放摄像头：

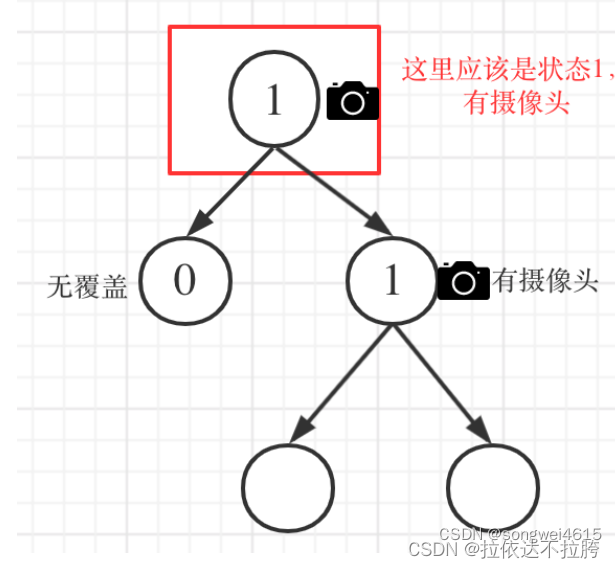
在这里插入图片描述

情况3：左右节点至少有一个有摄像头
如果是以下情况，其实就是左右孩子节点有一个有摄像头了，那么其父节点就应该是2（覆盖的状态）
情况4：头结点没有覆盖
以上都处理完了，递归结束之后，可能头结点还有一个无覆盖的情况，如图：

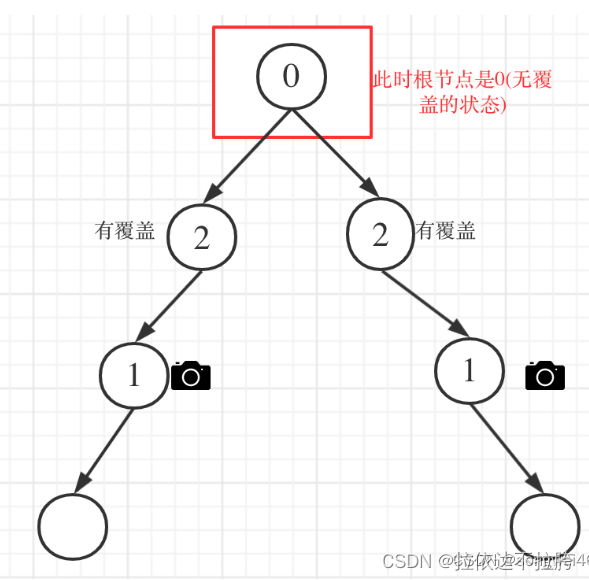
在这里插入图片描述

class Solution {
private:
    int result;
    int traversal(TreeNode* cur) {

        // 空节点，该节点有覆盖
        if (cur == NULL) return 2;

        int left = traversal(cur->left);    // 左
        int right = traversal(cur->right);  // 右

        // 情况1
        // 左右节点都有覆盖
        if (left == 2 && right == 2) return 0;

        // 情况2
        // left == 0 && right == 0 左右节点无覆盖
        // left == 1 && right == 0 左节点有摄像头，右节点无覆盖
        // left == 0 && right == 1 左节点有无覆盖，右节点摄像头
        // left == 0 && right == 2 左节点无覆盖，右节点覆盖
        // left == 2 && right == 0 左节点覆盖，右节点无覆盖
        if (left == 0 || right == 0) {
            result++;
            return 1;
        }

        // 情况3
        // left == 1 && right == 2 左节点有摄像头，右节点有覆盖
        // left == 2 && right == 1 左节点有覆盖，右节点有摄像头
        // left == 1 && right == 1 左右节点都有摄像头
        // 其他情况前段代码均已覆盖
        if (left == 1 || right == 1) return 2;

        // 以上代码我没有使用else，主要是为了把各个分支条件展现出来，这样代码有助于读者理解
        // 这个 return -1 逻辑不会走到这里。
        return -1;
    }

public:
    int minCameraCover(TreeNode* root) {
        result = 0;
        // 情况4
        if (traversal(root) == 0) { // root 无覆盖
            result++;
        }
        return result;
    }
};