文章目录
- DDPM
- 论文整体原理
- 前向扩散过程
- 反向扩散过程
- 模型训练过程
- 模型生成过程
- 概率分布视角
- 参数模型设置
- 论文结果分析
要想完成SD中从文字到图片的操作,必须要做到两步,第一步是理解文字输入包含的语义,第二步是利用语义引导图片的生成。下面我们从几篇论文入手,首先搞懂以假乱真的图片是如何生成的,再学会对自然语言的理解方式,也就弄懂了文生图的魔法是从何而来。最后,我们会看看SDXL、Control Net、Turbo以及LCM等变种分别是从哪些角度为SD锦上添花的。这里我们先从扩散讲起。
DDPM
这是解开图片生成之谜的第一把钥匙,原文是发表于NIPS2020的Denoising Diffusion Probabilistic Models,下面我们就如庖丁解牛般,尝试洞察里面的每一丝细节。
论文整体原理
先从标题说起,很久没有看到过这么简明扼要的论文名了,用三个词就完美概括了DDPM的核心思想,去噪(Denoising)是方法、扩散(Diffusion)是架构、概率(Probabilistic)是媒介。至于目的,当然是去生成以假乱真的图片。
图片生成不是什么新鲜事,VAE和GAN都是曾经的研究宠儿,它们在生成图片时都需要一步解压的操作,也就是从低维空间中获得关于图片的表征或概率分布,再使用解码器或生成器映射到高维的图片空间。而概率扩散可以被视为一个马尔科夫过程,马尔科夫链中不论是状态矩阵还是转移矩阵的大小都是固定的,因此扩散在一个固定的维度下进行,二者的区别如下:
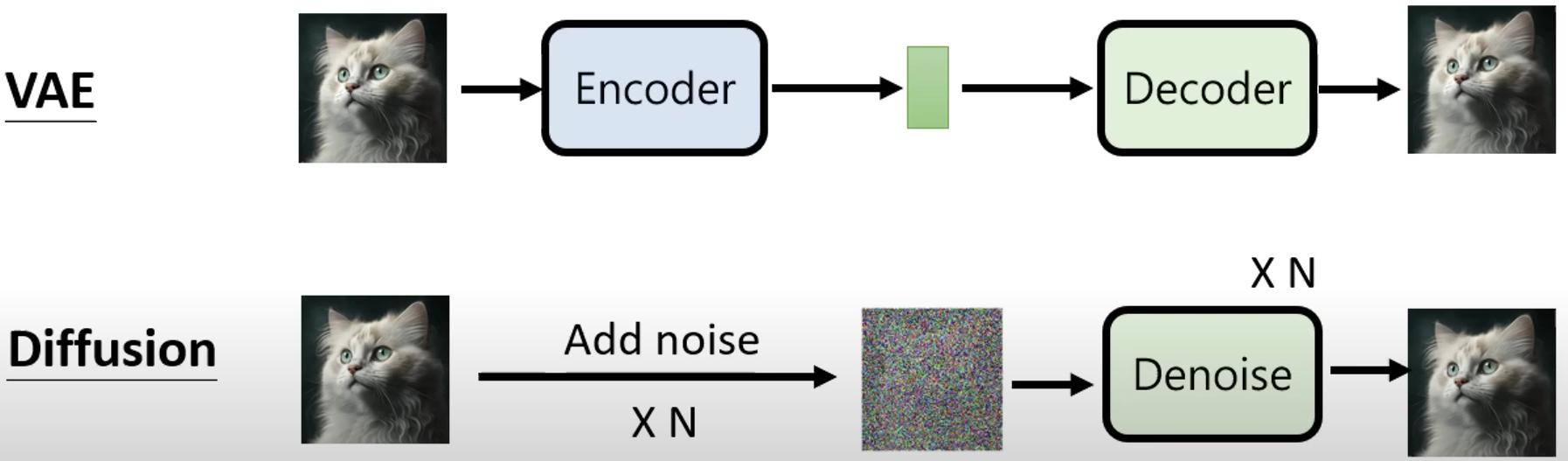
其在数学上的整体过程如下图所示:
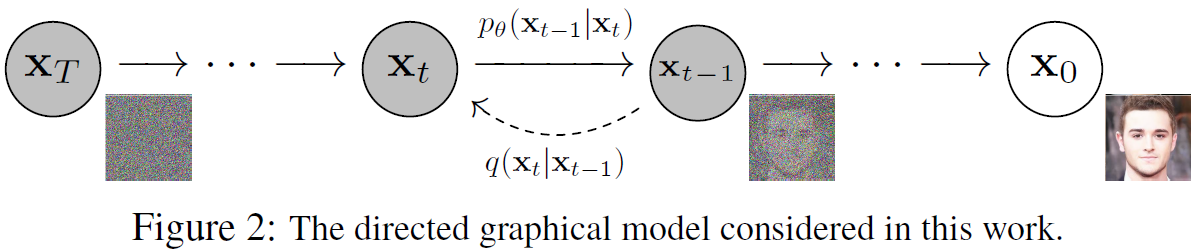
可以看出,这条链是双向的。从右到左称之为前向扩散,是一个逐渐给原始图片加入噪音的过程;从左到右是反向,也就是从噪音生成原始图片,也是DDPM图片生成能力的来源。
前向扩散过程
前向过程其实就是一个逐步给图片加噪音的过程,每一步都为原始图片加一点随机采样后的高斯噪声
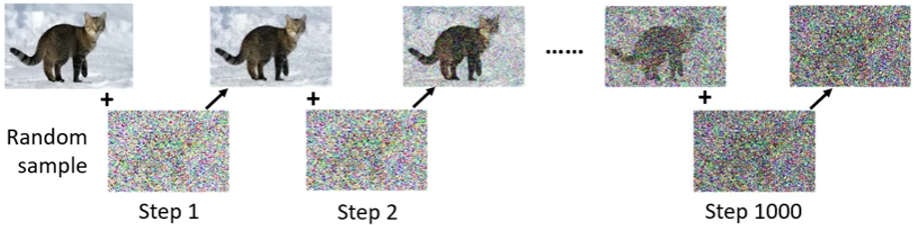
具体来说,其加噪的公式如下,从原图
x
0
x_{0}
x0按照系数
β
t
\beta_t
βt开始一步步加入噪声
ϵ
t
\epsilon_t
ϵt:
x
t
=
β
t
×
ϵ
t
+
1
−
β
t
×
x
t
−
1
\begin{equation} x_t=\sqrt{\beta_t} \times \epsilon_t+\sqrt{1-\beta_t} \times x_{t-1} \\ \end{equation}
xt=βt×ϵt+1−βt×xt−1
其中
ϵ
t
\epsilon_t
ϵt是符合标准正态分布的噪声,
β
t
\beta_t
βt是预先定义的一组超参数,数值逐渐增大以模拟扩散过程的不断加速
ϵ
t
∼
N
(
0
,
1
)
0
<
β
1
<
β
2
<
β
3
<
β
t
−
1
<
β
t
<
1
\begin{align} \epsilon_t &\sim N(0,1) \\ 0<\beta_1 &< \beta_2 < \beta_3 < \beta_{t-1} < \beta_t < 1 \end{align}
ϵt0<β1∼N(0,1)<β2<β3<βt−1<βt<1
上面的公式描述了单步迭代的过程,理论上,既然每一步的公式是固定的,那我们应该能求导出一步到位的公式,也就是如何从原图
x
0
x_{0}
x0直接得到
x
t
x_{t}
xt。为了简化计算,令
α
t
=
1
−
β
t
\alpha_t = 1-\beta_t
αt=1−βt,单步迭代的过程重写为:
x
t
=
1
−
α
t
×
ϵ
t
+
α
t
×
x
t
−
1
\begin{equation} x_t=\sqrt{1-\alpha_t} \times \epsilon_t+\sqrt{\alpha_t} \times x_{t-1} \\ \end{equation}
xt=1−αt×ϵt+αt×xt−1
其上一步的结果可以写为:
x
t
−
1
=
1
−
α
t
−
1
×
ϵ
t
−
1
+
α
t
−
1
×
x
t
−
2
\begin{equation} x_{t-1}=\sqrt{1-\alpha_{t-1}} \times \epsilon_{t-1}+\sqrt{\alpha_{t-1}} \times x_{t-2} \\ \end{equation}
xt−1=1−αt−1×ϵt−1+αt−1×xt−2
将式(5)代入式(4)后得:
x
t
=
a
t
(
1
−
a
t
−
1
)
ϵ
t
−
1
+
1
−
a
t
×
ϵ
t
+
a
t
a
t
−
1
×
x
t
−
2
\begin{equation} x_t=\sqrt{a_t\left(1-a_{t-1}\right)} \epsilon_{t-1}+\sqrt{1-a_t} \times \epsilon_t+\sqrt{a_t a_{t-1}} \times x_{t-2} \end{equation}
xt=at(1−at−1)ϵt−1+1−at×ϵt+atat−1×xt−2
这里需要回顾一下正态分布的运算公式:如果一个正态分布的随机变量 X X X服从 N ( μ , σ 2 ) N(μ, σ^2) N(μ,σ2),即均值是 μ μ μ,方差是 σ 2 σ^2 σ2,给定常数 C C C和另一个变量 Z Z Z服从 N ( μ 1 , σ 1 2 ) N(μ_1, σ_1^2) N(μ1,σ12),则有:
- 对新分布 Y = C × X Y=C\times X Y=C×X, Y Y Y的均值为 C × μ C\times μ C×μ,方差为 C 2 × σ 2 C^2\times σ^2 C2×σ2
- 对新分布 Y = C + X Y=C+X Y=C+X, Y Y Y的均值为 C + μ C+μ C+μ,方差为 σ 2 σ^2 σ2
- 对新分布 Y = X + Z Y=X+Z Y=X+Z, Y Y Y的均值为 μ + μ 1 μ+μ_1 μ+μ1,方差为 σ 2 + σ 1 2 σ^2+ σ_1^2 σ2+σ12
- 对新分布 Y = X × Z Y=X\times Z Y=X×Z, Y Y Y不再是正态分布,而变得更为复杂
式(6)中的前两项本质上是将两个独立采样得到的满足标准正态分布的噪声乘以权重后相加,套用上述运算规则,可以得到一个新的概率分布,并且可以知道这是一个均值为0,方差为
1
−
a
t
a
t
−
1
1-a_t a_{t-1}
1−atat−1的正态分布。运用重参数化技巧,我们可以基于一个满足标准正态分布的随机变量
ϵ
\epsilon
ϵ来重写:
x
t
=
1
−
a
t
a
t
−
1
ϵ
+
a
t
a
t
−
1
×
x
t
−
2
\begin{equation} x_t=\sqrt{1-a_t a_{t-1}} \epsilon+\sqrt{a_t a_{t-1}} \times x_{t-2} \end{equation}
xt=1−atat−1ϵ+atat−1×xt−2
接着将
x
t
−
2
x_{t-2}
xt−2关于
x
t
−
3
x_{t-3}
xt−3的递推式带入上式,在多次使用重参数化和数学归纳法之后,可以得到以下的多步递推式:
x
t
=
1
−
a
t
a
t
−
1
a
t
−
2
…
a
t
−
(
k
−
2
)
a
t
−
(
k
−
1
)
ϵ
+
a
t
a
t
−
1
a
t
−
2
…
a
t
−
(
k
−
2
)
a
t
−
(
k
−
1
)
x
t
−
k
\begin{equation} \begin{gathered} x_t=\sqrt{1-a_t a_{t-1} a_{t-2} \ldots a_{t-(k-2)} a_{t-(k-1)}} \epsilon+ \\ \sqrt{a_t a_{t-1} a_{t-2} \ldots a_{t-(k-2)} a_{t-(k-1)}} x_{t-k} \end{gathered}\end{equation}
xt=1−atat−1at−2…at−(k−2)at−(k−1)ϵ+atat−1at−2…at−(k−2)at−(k−1)xt−k
取
k
=
t
,
α
ˉ
t
=
∏
i
=
1
t
α
i
k=t, \bar{\alpha}_{t} = \prod_{i=1}^{t} \alpha_{i}
k=t,αˉt=∏i=1tαi,则一步到位的公式可以写作:
x
t
=
1
−
α
ˉ
t
×
ϵ
+
α
ˉ
t
×
x
0
\begin{equation} x_t=\sqrt{1-\bar{\alpha}_{t} } \times \epsilon+\sqrt{\bar{\alpha}_{t} } \times x_{0} \\ \end{equation}
xt=1−αˉt×ϵ+αˉt×x0
反向扩散过程
反向扩散本质上就是在计算这样一个概率
P
(
x
t
−
1
∣
x
t
)
P(x_{t-1}\mid x_t)
P(xt−1∣xt),也就是去掉一部分噪音,让其跟目标图片更接近一些。

这里需要回顾一下贝叶斯公式,它描述了在给定相关证据的情况下,某个假设的概率是如何更新的。
贝叶斯公式的基本形式如下: P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)
其中:
- P ( A ∣ B ) P(A|B) P(A∣B) 是在事件B发生的条件下事件A发生的概率,称为后验概率。
- P ( B ∣ A ) P(B|A) P(B∣A) 是在事件A发生的条件下事件B发生的概率,称为似然概率。
- P ( A ) P(A) P(A) 是事件A发生的概率,称为先验概率。
- P ( B ) P(B) P(B) 是事件B发生的概率,称之为证据。
根据贝叶斯公式,将概率进行拆解
P
(
x
t
−
1
∣
x
t
)
=
P
(
x
t
∣
x
t
−
1
)
P
(
x
t
−
1
)
P
(
x
t
)
\begin{equation} P\left(x_{t-1} \mid x_t\right)=\frac{P\left(x_t \mid x_{t-1}\right)P\left(x_{t-1}\right)}{P\left(x_t\right)} \end{equation}
P(xt−1∣xt)=P(xt)P(xt∣xt−1)P(xt−1)
我们知道
x
t
−
1
x_{t-1}
xt−1和
x
t
x_t
xt都不是凭空产生的,而是从
x
0
x_0
x0一步步转换来的,并且遵循马尔可夫链原理,即每一步只与上一步有关,而与最开始的
x
0
x_0
x0无关,因此在条件概率公式里加上
x
0
x_0
x0对结果无影响。所以,计算目标可以转换为
P
(
x
t
−
1
∣
x
t
,
x
0
)
P(x_{t-1} \mid x_t, x_0)
P(xt−1∣xt,x0),在上式中统一加上一个
x
0
x_0
x0后可得:
P
(
x
t
−
1
∣
x
t
,
x
0
)
=
P
(
x
t
∣
x
t
−
1
)
P
(
x
t
−
1
∣
x
0
)
P
(
x
t
∣
x
0
)
\begin{equation} P\left(x_{t-1} \mid x_t, x_0\right)=\frac{P\left(x_t \mid x_{t-1}\right) P\left(x_{t-1} \mid x_0\right)}{P\left(x_t \mid x_0\right)} \end{equation}
P(xt−1∣xt,x0)=P(xt∣x0)P(xt∣xt−1)P(xt−1∣x0)
也可以通过条件概率公式推导出来这个结论:
P
(
x
t
−
1
∣
x
t
,
x
0
)
=
P
(
x
t
−
1
,
x
t
,
x
0
)
P
(
x
t
,
x
0
)
=
P
(
x
t
∣
x
t
−
1
)
P
(
x
t
−
1
∣
x
0
)
P
(
x
0
)
P
(
x
t
∣
x
0
)
P
(
x
0
)
=
P
(
x
t
∣
x
t
−
1
)
P
(
x
t
−
1
∣
x
0
)
P
(
x
t
∣
x
0
)
\begin{equation} \begin{gathered} P\left(x_{t-1} \mid x_t, x_0\right)=\frac{P\left(x_{t-1}, x_t, x_0\right)}{P\left(x_t, x_0\right)}= \\ \frac{P\left(x_t \mid x_{t-1}\right) P\left(x_{t-1} \mid x_0\right) P\left(x_0\right)}{P\left(x_t \mid x_0\right) P\left(x_0\right)}= \\\frac{P\left(x_t \mid x_{t-1}\right) P\left(x_{t-1} \mid x_0\right)}{P\left(x_t \mid x_0\right)} \end{gathered}\end{equation}
P(xt−1∣xt,x0)=P(xt,x0)P(xt−1,xt,x0)=P(xt∣x0)P(x0)P(xt∣xt−1)P(xt−1∣x0)P(x0)=P(xt∣x0)P(xt∣xt−1)P(xt−1∣x0)
接下来,根据正态分布运算公式分别计算
P
(
x
t
∣
x
t
−
1
)
P
(
x
t
−
1
∣
x
0
)
P
(
x
t
∣
x
0
)
\frac{P\left(x_t \mid x_{t-1}\right) P\left(x_{t-1} \mid x_0\right)}{P\left(x_t \mid x_0\right)}
P(xt∣x0)P(xt∣xt−1)P(xt−1∣x0)中各项的概率分布,根据式(4)有
P
(
x
t
∣
x
t
−
1
)
∼
N
(
α
t
×
x
t
−
1
,
1
−
α
t
)
P\left(x_t \mid x_{t-1}\right)\sim N(\sqrt{\alpha_t} \times x_{t-1},1-\alpha_t)
P(xt∣xt−1)∼N(αt×xt−1,1−αt),根据式(9)有
P
(
x
t
−
1
∣
x
0
)
∼
N
(
α
ˉ
t
−
1
×
x
0
,
1
−
α
ˉ
t
−
1
)
P\left(x_{t-1} \mid x_0\right)\sim N(\sqrt{\bar{\alpha}_{t-1} } \times x_{0},1-\bar{\alpha}_{t-1})
P(xt−1∣x0)∼N(αˉt−1×x0,1−αˉt−1)及
P
(
x
t
∣
x
0
)
∼
N
(
α
ˉ
t
×
x
0
,
1
−
α
ˉ
t
)
P\left(x_{t} \mid x_0\right)\sim N(\sqrt{\bar{\alpha}_{t} } \times x_{0},1-\bar{\alpha}_{t})
P(xt∣x0)∼N(αˉt×x0,1−αˉt)。
由于这是多个正态分布间的乘除操作,因此不能再套用加减情况下的规则计算联合分布,而要将均值
μ
\mu
μ和标准差
σ
\sigma
σ代入正态分布的概率密度函数
f
(
x
)
=
1
σ
2
π
e
−
1
2
(
x
−
μ
σ
)
2
f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}
f(x)=σ2π1e−21(σx−μ)2中计算具体概率值再反向代入回来,经过一番简单但繁琐的整理,可以得到下面的公式:
P
(
x
t
−
1
∣
x
t
,
x
0
)
∼
N
(
a
t
(
1
−
a
ˉ
t
−
1
)
1
−
a
ˉ
t
x
t
+
a
ˉ
t
−
1
(
1
−
a
t
)
1
−
a
ˉ
t
x
0
,
β
t
(
1
−
a
ˉ
t
−
1
)
1
−
a
ˉ
t
)
=
N
(
a
t
(
1
−
a
ˉ
t
−
1
)
1
−
a
ˉ
t
x
t
+
a
ˉ
t
−
1
(
1
−
a
t
)
1
−
a
ˉ
t
×
x
t
−
1
−
a
ˉ
t
×
ϵ
a
ˉ
t
,
β
t
(
1
−
a
ˉ
t
−
1
)
1
−
a
ˉ
t
)
=
N
(
1
α
t
(
x
t
−
1
−
α
t
1
−
α
t
ˉ
ϵ
)
,
β
t
(
1
−
a
ˉ
t
−
1
)
1
−
a
ˉ
t
)
\begin{equation} \begin{gathered} P(x_{t-1} \mid x_t, x_0) \sim N(\frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t} x_t+ \\\frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t} x_0, \frac{\beta_t(1-\bar{a}_{t-1})}{1-\bar{a}_t}) =\\ N(\frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t} x_t+ \frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t} \times \\ \frac{x_t-\sqrt{1-\bar{a}_t} \times \epsilon}{\sqrt{\bar{a}_t}}, \frac{\beta_t(1-\bar{a}_{t-1})}{1-\bar{a}_t}) = \\ N(\frac{1}{\sqrt{\alpha_t}}(x_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha_t}}}\epsilon),\frac{\beta_t(1-\bar{a}_{t-1})}{1-\bar{a}_t}) \end{gathered}\end{equation}
P(xt−1∣xt,x0)∼N(1−aˉtat(1−aˉt−1)xt+1−aˉtaˉt−1(1−at)x0,1−aˉtβt(1−aˉt−1))=N(1−aˉtat(1−aˉt−1)xt+1−aˉtaˉt−1(1−at)×aˉtxt−1−aˉt×ϵ,1−aˉtβt(1−aˉt−1))=N(αt1(xt−1−αtˉ1−αtϵ),1−aˉtβt(1−aˉt−1))
这个式子只是在描述概率的分布情况,运用重参数化方法,可以将
x
t
−
1
x_{t-1}
xt−1表示为如下的形式,其中
z
z
z是满足标准正态分布的随机变量:
x
t
−
1
=
1
α
t
(
x
t
−
1
−
α
t
1
−
α
t
ˉ
ϵ
)
+
β
t
(
1
−
a
ˉ
t
−
1
)
1
−
a
ˉ
t
z
\begin{equation} \begin{gathered} x_{t-1} = \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha_t}}}\epsilon) + \sqrt{\frac{\beta_t(1-\bar{a}_{t-1})}{1-\bar{a}_t}}z \end{gathered}\end{equation}
xt−1=αt1(xt−1−αtˉ1−αtϵ)+1−aˉtβt(1−aˉt−1)z
模型训练过程
从前向扩散的过程中我们可以发现,随着模型步数的增加,原图上覆盖的噪音越来越大,新图与原图间的区别也越来越大。这里我们训练一个噪音预测器,让它能根据当前步数及加噪图像,预测出加的噪声,一个简单的图示如下。
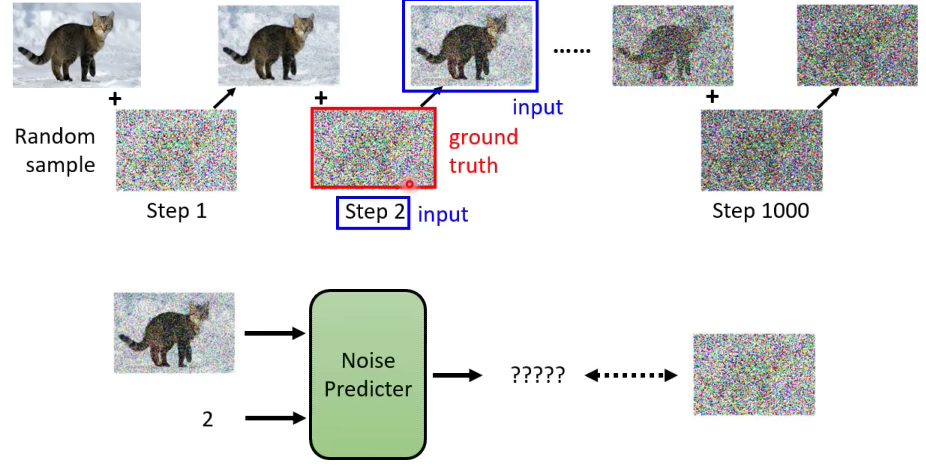
在实际训练时,为了简化计算,我们根据式(9)实现加噪图像的一步到位式生成,令
ϵ
θ
\epsilon_\theta
ϵθ为噪音预测器,训练目标是通过MSE来最小化预测噪音和真实噪音之间的差距。

模型生成过程
在训练好一个噪音预测器后,根据式(14),可以很轻松地写出下面的模型生成算法,其中
σ
t
z
\sigma_tz
σtz对应要加的方差项。

在这里你可能会有些疑问,
x
T
x_T
xT不是由
x
0
x_0
x0一步步生成出来的吗,为什么这里可以直接用一个正态分布的随机噪声来代替呢。我们回顾一下式(9),由于
α
ˉ
t
=
∏
i
=
1
t
α
i
\bar{\alpha}_{t} = \prod_{i=1}^{t} \alpha_{i}
αˉt=∏i=1tαi,当
t
t
t取极大时,由于
α
i
\alpha_{i}
αi是位于01之间的小数,因此其累乘后趋近于0,也就是
x
t
≈
ϵ
x_t \approx \epsilon
xt≈ϵ。
如果还是不够直观,可以想象这样一个过程:你手头有这样一个纯白的石膏像,你一层层在它上面抹石膏,直到变成一个浑圆的坤蛋。然后你再从这个坤蛋开始,一层层剥离石膏,直到复原出那个你心中的偶像。尽管坤蛋中既看不出篮球也看不出中分,但它们的形状已经牢牢刻进了你鸡爪的肌肉记忆之中。这,就是ikun 扩散。

在这里,我们不妨再重新审视一下式(1),为什么两个分布加权时,要在系数前面加根号呢。如果把
t
t
t看得足够大,那么
x
t
−
1
x_{t-1}
xt−1和
ϵ
t
\epsilon_t
ϵt都服从标准高斯分布,它们相加之后的新分布的方差就是系数的平方和。为了保证扩散过程的稳定,也就是每一步的结果大致服从相似的分布,需要保持方差的稳定,所以要求系数的平方和始终为一,否则方差就会变成0或者无穷大,这跟batch norm的意思有点像。(当然上面的想法使用了循环论证,并不严谨,差不多这意思)。
概率分布视角
看过论文的朋友可能会有点奇怪,你这上面说的和论文里写的好像是两码事啊,论文里那些一大长串完全看不懂的公式被你吃了?其实上面的内容是从较为直观的视角展示扩散过程的,而为了更深入地理解其数学原理,接下来我们从概率分布的视角去重新审视DDPM,并与论文中的公式做个对应。
不管是VAE还是DDPM,图像生成模型的最终目标都是让生成图像的概率分布与真实图像的分布尽可能接近。以VAE为例,给定随机输入的分布
z
z
z,使用极大似然估计法优化生成的图像,也就是让KL距离尽可能接近。
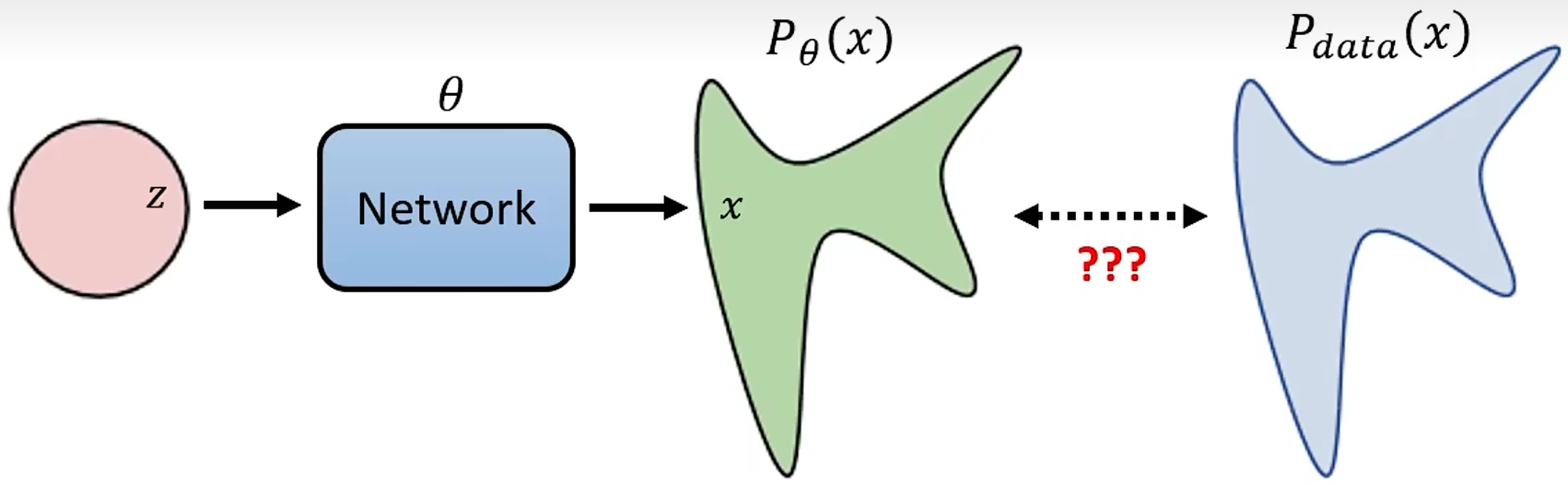

针对特定的
x
x
x,通过变分推断法计算其下界

这里的
z
z
z是VAE的随机噪声,放到DDPM里则是加了噪音之后的
x
1
,
.
.
.
,
x
T
x_1, ...,x_T
x1,...,xT,也就是论文里面的公式(3)
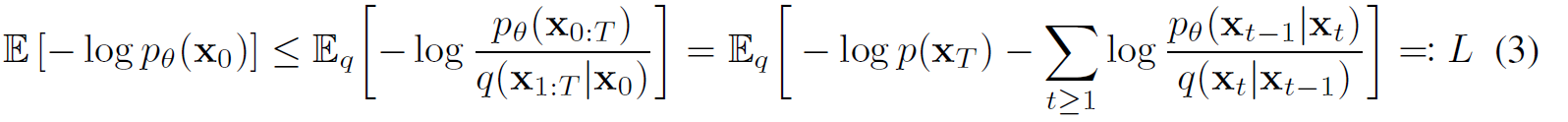
对上式做变换,并转换成KL散度的形式,得到下面的论文公式(5)
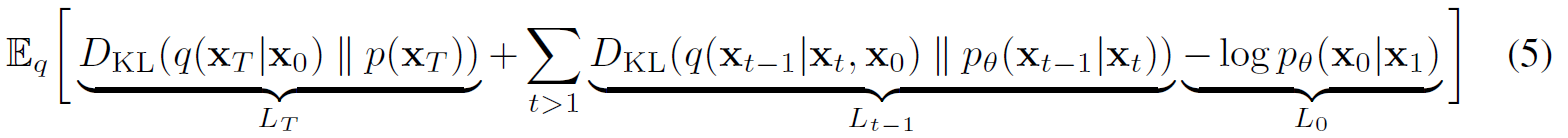
最小化论文公式(5),也就是最小化
L
T
L_T
LT和
L
t
−
1
L_{t-1}
Lt−1,最大化
L
0
L_0
L0。
针对
L
T
L_T
LT对应的噪音分布一致的目标,由于
β
t
\beta_t
βt可以看做是常数项,因此
L
T
L_T
LT可以视为常数项忽略。
针对
L
t
−
1
L_{t-1}
Lt−1对应的去噪过程一致的目标,首先这两项都是高斯分布,然后令它们的方差一样,根据KL散度的计算公式得到下面的论文公式(8),其中
C
C
C是常数:

上式主要目的是让网络学习到的均值和后验分布的均值一致,我们把后验分布的均值公式代入之后得到论文公式(9-10)

根据定义将均值预测函数
μ
θ
\mu_\theta
μθ转换为噪音预测函数
μ
ϵ
\mu_\epsilon
μϵ,得到论文公式(11-12)


针对
L
0
L_0
L0对应的真实数据生成的目标,论文中提到要将[0, 255]的像素值归一化到[-1, 1]间以确保扩散的稳定性,因此可以用论文公式(13)来优化

将
L
0
L_0
L0和
L
t
−
1
L_{t-1}
Lt−1对应的情况合并后,就得到了以下训练目标:

以上就是论文中的理论部分了,只能说确实难懂,建议多看几遍吧。
参数模型设置
论文将总采样步数
T
T
T设为1000,令加噪系数从
β
1
=
1
0
−
4
\beta_1 = 10^{-4}
β1=10−4到
β
1
000
=
0.02
\beta_1000 = 0.02
β1000=0.02间线性增加。
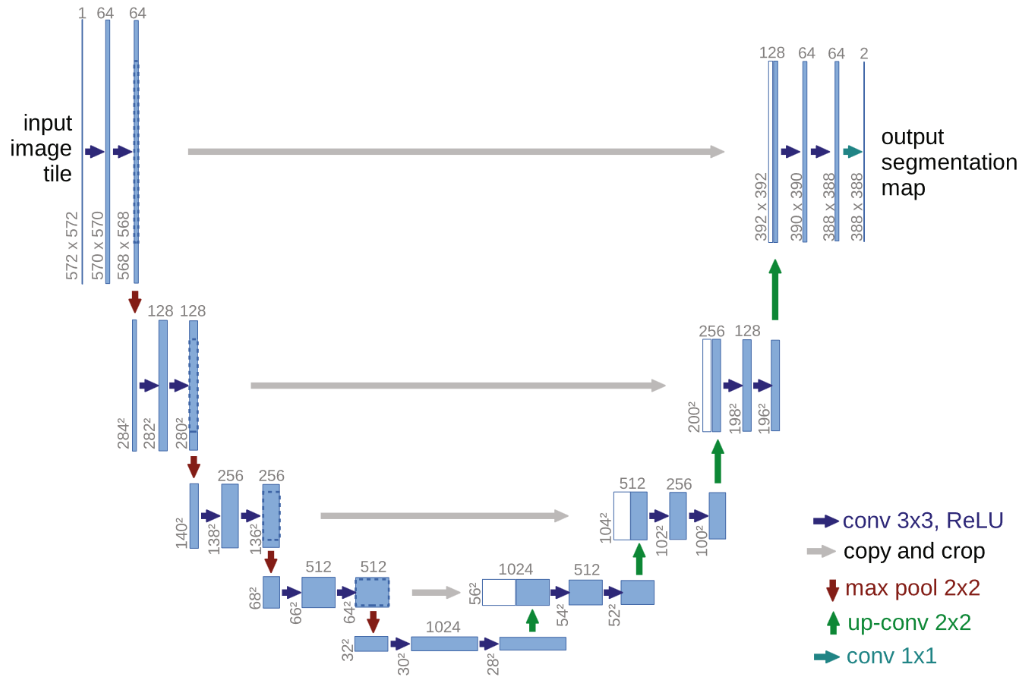
论文使用了上图所示的U-Net backbone作为去噪器的实现,其实现时有以下几个要点:
- 使用transformer中的正弦位置编码即sinusoidal position embedding编码输入时间步,并在各层中共享。
- 采用GroupNorm进行归一化。
- 引入残差块。
- 在16×16的特征图上采用自注意力机制。
论文结果分析
- 总体生成质量比较

- 预测噪音比预测均值更好

- 与自回归模型比较
论文提出了一种很新奇的想法,如果让加噪步数等于总像素数,加噪音时依次屏蔽当前步数对应的像素坐标,这样每次加噪音时都利用了被屏蔽像素的真实值,就转化成了自回归模型。 - 插值加噪过程
反向扩散时,令中间结果是不同图像的加权和,即 x ˉ t = ( 1 − λ ) x 0 + λ x 0 ′ \bar x_t = (1-\lambda)x_0+\lambda x'_0 xˉt=(1−λ)x0+λx0′,可以生成融合两张图的图片。