从Bellman-Ford开始

• 对于所有边权都大于等于0的图，任意两个顶点之间的最短路，显然不会经过重复的顶点或者边。也就是说任意一条最短路经过的定点数不会超过n个，边不会超过n-1条边
• 而对于有边权为负的图，有可能图中会存在负环，此时途径负环的最短路没有意义。

核心思想

$Bellman-Ford$的核心思想是松弛操作，即对于边$(u,v)$,用$dist(u)和l(u,v)$的和尝试更新$dist(v):$
$$dist(v)=min(dist(v),dist(u)+l(u,v))$$

$Bellman-Ford$所做的，就是不断尝试对图上每一条边进行松弛操作。

---

我们会进行多次迭代，每进行一次迭代，就对图上所有的边都尝试进行一次松弛操作，当一次迭代中没有点的$dist$发生改变时，算法停止。

---

模拟算法执行过程

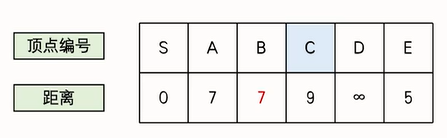
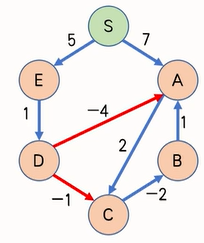
在每次迭代中，遍历所有边，尝试进行松弛操作

---

---

因为这里$B$还是正无穷，还没找到从起点到$B$的最短路，这样通过当前的$B$更新其他点是没有意义（这也是后面$spfa$优化的关键）

---

---

---

---

至此第一轮迭代完成，下面是第二轮迭代

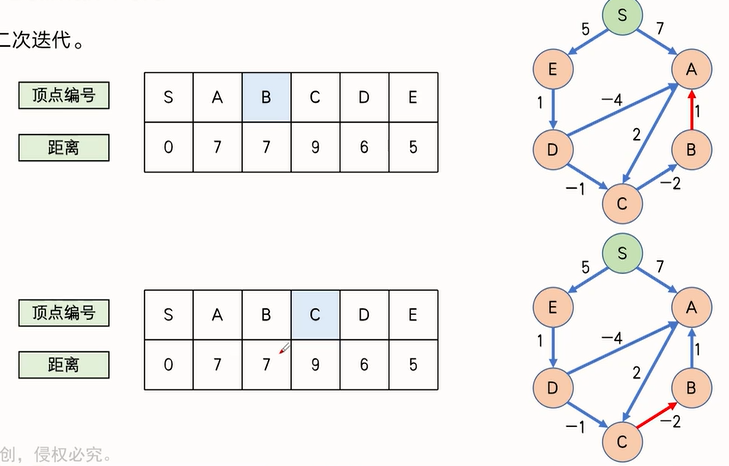
第四次迭代已经什么都更新不了了

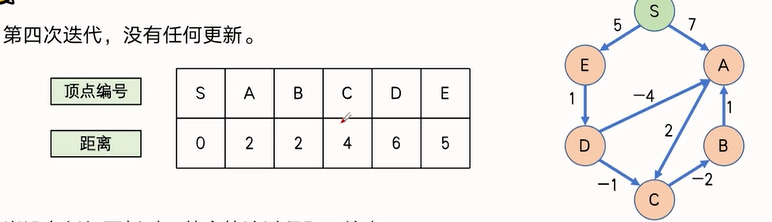
时间复杂度

在最短路存在的情况下（图中不存在负环），由于一次迭代会使最短路的边数至少加$1$，而$S$到每个顶点的最短路经过的边数最多为$n-1$，因此整个算法最多会进行$n-1$轮迭代，每一轮迭代的复杂度为$O(m)$(每条边枚举到一次),所以总的时间复杂度为$O(nm)$

• 当从$S$点出发能到达一个负环时，就会进行n论以上的迭代

模板

int n, m;       // n表示点数，m表示边数
int dist[N];        // dist[x]存储1到x的最短路距离

struct Edge     // 边，a表示出点，b表示入点，w表示边的权重
{
    int a, b, w;
}edges[M];

// 求1到n的最短路距离，如果无法从1走到n，则返回-1。
int bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    // 如果第n次迭代仍然会松弛三角不等式，就说明存在一条长度是n+1的最短路径，由抽屉原理，路径中至少存在两个相同的点，说明图中存在负权回路。
    for (int i = 0; i < n; i ++ )
    {
        for (int j = 0; j < m; j ++ )
        {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            if (dist[b] > dist[a] + w)
                dist[b] = dist[a] + w;
        }
    }

    if (dist[n] > 0x3f3f3f3f / 2) return -1;
    return dist[n];
}

spfa

spfa优化的思想

$spfa$是通过队列来优化$bellman-ford$算法
在每一次迭代时，只有在上一次迭代中被更新了距离的点，才有可能去更新其他节点。因此，在每一次迭代时，我们将更新过距离的顶点加入一个队列（如果顶点已经在队列里则不加），在下一次迭代时，只需要遍历队列中的顶点连出去的边即可。

• 在实际实现过程中我们不关心具体是那一次迭代。

模板

vector<vector<pii>>g(n+1);
rep(i,1,m){
	int u,v,w;
	cin>>u>>v>>w;
	g[u].pb({v,w});
	g[v].pb({u,w});
}
vector<vector<int>>inq(n+1);
vector<vector<int>>d(n+1,0x3f3f3f3f);
queue<int>q;
d[1]=0;
inq[1]=1;
q.push(1);
//跑一遍最短路
while(q.size()){
	auto t=q.front();
	q.pop();
	int u=t.x,cnt=t.y;
	inq[u]=0;
	for(auto it:g[u]){
		int v=it.x,w=it.y;
		//松弛操作，或者其他变形具体问题具体分析
		if(满足松弛){
			//更新
			if(!inq[v]){
				inq[v]=1;
				q.push(v);
			}
		}
	}
}