1314:【例3.6】过河卒(Noip2002)
时间限制: 1000 ms 内存限制: 65536 KB
提交数: 40991 通过数: 17884
【题目描述】
棋盘上A点有一个过河卒,需要走到目标B点。卒行走的规则:可以向下、或者向右。同时在棋盘上的某一点有一个对方的马(如C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点,如图3-1中的C点和P1,……,P8,卒不能通过对方马的控制点。棋盘用坐标表示,A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的,C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。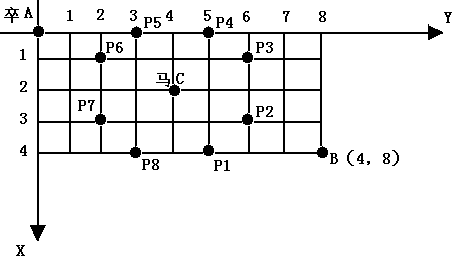
【输入】
给出n、m和C点的坐标。
【输出】
从A点能够到达B点的路径的条数。
【输入样例】
8 6 0 4
【输出样例】
1617
用了动态规划,先把马能走的八个方向记录为过河卒不能走的地方,再把上面和左边两条边进行判断有几条路能到达,最后再从左到右从上到下计算每个格子有几条路能到达,输出地图右下角的格子的数。
#include<bits/stdc++.h>
using namespace std;
long long n,m,x,y,a[101][101];
int main()
{
cin>>n>>m>>x>>y;
a[x][y]=-1;
if(x+2<=20&&y+1<=20)
a[x+2][y+1]=-1;
if(x+1<=20&&y+2<=20)
a[x+1][y+2]=-1;
if(x-1>=0&&y+2<=20)
a[x-1][y+2]=-1;
if(x-2>=0&&y+1<=20)
a[x-2][y+1]=-1;
if(x+2<=20&&y-1>=0)
a[x+2][y-1]=-1;
if(x+1<=20&&y-2>=0)
a[x+1][y-2]=-1;
if(x-2>=0&&y-1>=0)
a[x-2][y-1]=-1;
if(x-1>=0&&y-2>=0)
a[x-1][y-2]=-1;
a[0][0]=1;
for(int i=1;i<=n;i++)
{
if(a[i-1][0]<=0&&a[i][0]!=-1)
a[i][0]=0;
else if(a[i][0]!=-1)
a[i][0]=1;
}
for(int i=1;i<=m;i++)
{
if(a[0][i-1]<=0&&a[0][i]!=-1)
a[0][i]=0;
else if(a[0][i]!=-1)
a[0][i]=1;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(a[i][j]!=-1&&a[i-1][j]==-1&&a[i][j-1]!=-1)
{
a[i][j]=a[i][j-1];
}
if(a[i][j]!=-1&&a[i][j-1]==-1&&a[i-1][j]!=-1)
{
a[i][j]=a[i-1][j];
}
if(a[i][j]!=-1&&a[i-1][j]!=-1&&a[i][j-1]!=-1)
{
a[i][j]=a[i-1][j]+a[i][j-1];
}
}
}
// for(int i=0;i<=n;i++)
// {
// for(int j=0;j<=m;j++)
// {
// cout<<setw(7)<<a[i][j];
// }
// cout<<endl;
// }
cout<<a[n][m];
}