本文为Python算法题集之一的代码示例

题101：对称二叉树

1. 示例说明

• 给你一个二叉树的根节点 root ， 检查它是否轴对称。

  示例 1：

  

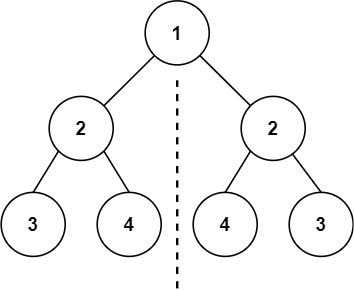
  输入：root = [1,2,2,3,4,4,3]
  输出：true
  

  示例 2：

  

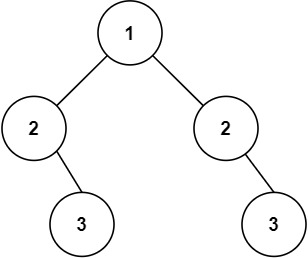
  输入：root = [1,2,2,null,3,null,3]
  输出：false
  

  提示：

  • 树中节点数目在范围 [1, 1000] 内
  • -100 <= Node.val <= 100

  **进阶：**你可以运用递归和迭代两种方法解决这个问题吗？

---

2. 题目解析

- 题意分解

1. 本题为检查二叉树是否对称
2. 基本的设计思路是深度优先算法【DFS（Depth-First Search）】、广度有限算法【BFS（Breadth-First Search）】

- 优化思路

1. 通常优化：减少循环层次

2. 通常优化：增加分支，减少计算集

3. 通常优化：采用内置算法来提升计算速度

4. 分析题目特点，分析最优解

   1. 可以考虑使用专门的队列结构deque

---

- 测量工具

• 本地化测试说明：LeetCode网站测试运行时数据波动很大，因此需要本地化测试解决这个问题
• CheckFuncPerf（本地化函数用时和内存占用测试模块）已上传到CSDN，地址：Python算法题集_检测函数用时和内存占用的模块
• 本题本地化超时测试用例自己生成，详见【最优算法章节】

---

3. 代码展开

1) 标准求解【DFS递归】

采用递归计算是否为对称二叉树

性能良好，超过80%

import CheckFuncPerf as cfp

class Solution:
 def isSymmetric_base(self, root):
     def dfscheck(left, right):
         if left is None and right is None:
             return True
         if left is None or right is None:
             return False
         if left.val != right.val:
             return False
         return dfscheck(left.left, right.right) and dfscheck(left.right, right.left)
     if root is None:
         return True
     return dfscheck(root.left, root.right)

aroot = generate_symmetry_binary_tree(ilen)
aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.isSymmetric_base, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result']))

# 运行结果
函数 isSymmetric_base 的运行时间为 45.00 ms；内存使用量为 4.00 KB 执行结果 = True

2) 改进版一【BFS迭代】

使用列表结构【list】作为堆栈，实现BFS搜索进行对称二叉树判断，性能相当低下

马马虎虎，超过59%

import CheckFuncPerf as cfp

class Solution:
 def isSymmetric_ext1(self, root):
     if root is None:
         return True
     if root.left is None and root.right is None:
         return True
     queue_nodes = [(root.left, root.right)]
     while queue_nodes:
         left, right = queue_nodes.pop(0) 
         if left is None and right is None:
             continue
         if left is None or right is None:
             return False
         if left.val != right.val:
             return False
         queue_nodes.append((left.left, right.right))
         queue_nodes.append((left.right, right.left))
     return True

aroot = generate_symmetry_binary_tree(ilen)
aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.isSymmetric_ext1, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result']))

# 运行结果
函数 isSymmetric_ext1 的运行时间为 3408.59 ms；内存使用量为 1732.00 KB 执行结果 = True

3) 改进版二【BFS迭代+deque】

使用高效双端队列结构【deque】作为堆栈，实现BFS搜索进行对称二叉树判断，性能有所改进

马马虎虎，超过59%

import CheckFuncPerf as cfp

class Solution:
 def isSymmetric_ext2(self, root):
     from collections import deque
     deque_tree = deque()
     deque_tree.append((root, root))
     while deque_tree:
         left, right = deque_tree.popleft()
         if not left and not right:
             continue
         if not left or not right:
             return False
         if left.val != right.val:
             return False
         deque_tree.append((left.left, right.right))
         deque_tree.append((left.right, right.left))
     return True

aroot = generate_symmetry_binary_tree(ilen)
aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.isSymmetric_ext2, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result']))

# 运行结果
函数 isSymmetric_ext2 的运行时间为 304.58 ms；内存使用量为 2436.00 KB 执行结果 = True

---

4. 最优算法

根据本地日志分析，最优算法为第1种方式【DFS递归】isSymmetric_base

ilen = 18
def generate_symmetry_binary_tree(ilevel):
    if ilevel <= 0:
        return None
    root = TreeNode(ilevel)
    left = generate_symmetry_binary_tree(ilevel - 1)
    right = generate_symmetry_binary_tree(ilevel - 1)
    root.left = left
    root.right = right
    return root
aroot = generate_symmetry_binary_tree(ilen)
aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.isSymmetric_base, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result']))
result = cfp.getTimeMemoryStr(Solution.isSymmetric_ext1, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result']))
result = cfp.getTimeMemoryStr(Solution.isSymmetric_ext2, aSolution, aroot)
print(result['msg'], '执行结果 = {}'.format(result['result']))


# 算法本地速度实测比较
函数 isSymmetric_base 的运行时间为 45.00 ms；内存使用量为 4.00 KB 执行结果 = True
函数 isSymmetric_ext1 的运行时间为 3408.59 ms；内存使用量为 1732.00 KB 执行结果 = True
函数 isSymmetric_ext2 的运行时间为 304.58 ms；内存使用量为 2436.00 KB 执行结果 = True

一日练，一日功，一日不练十日空

may the odds be ever in your favor ~