文章目录
- 简介
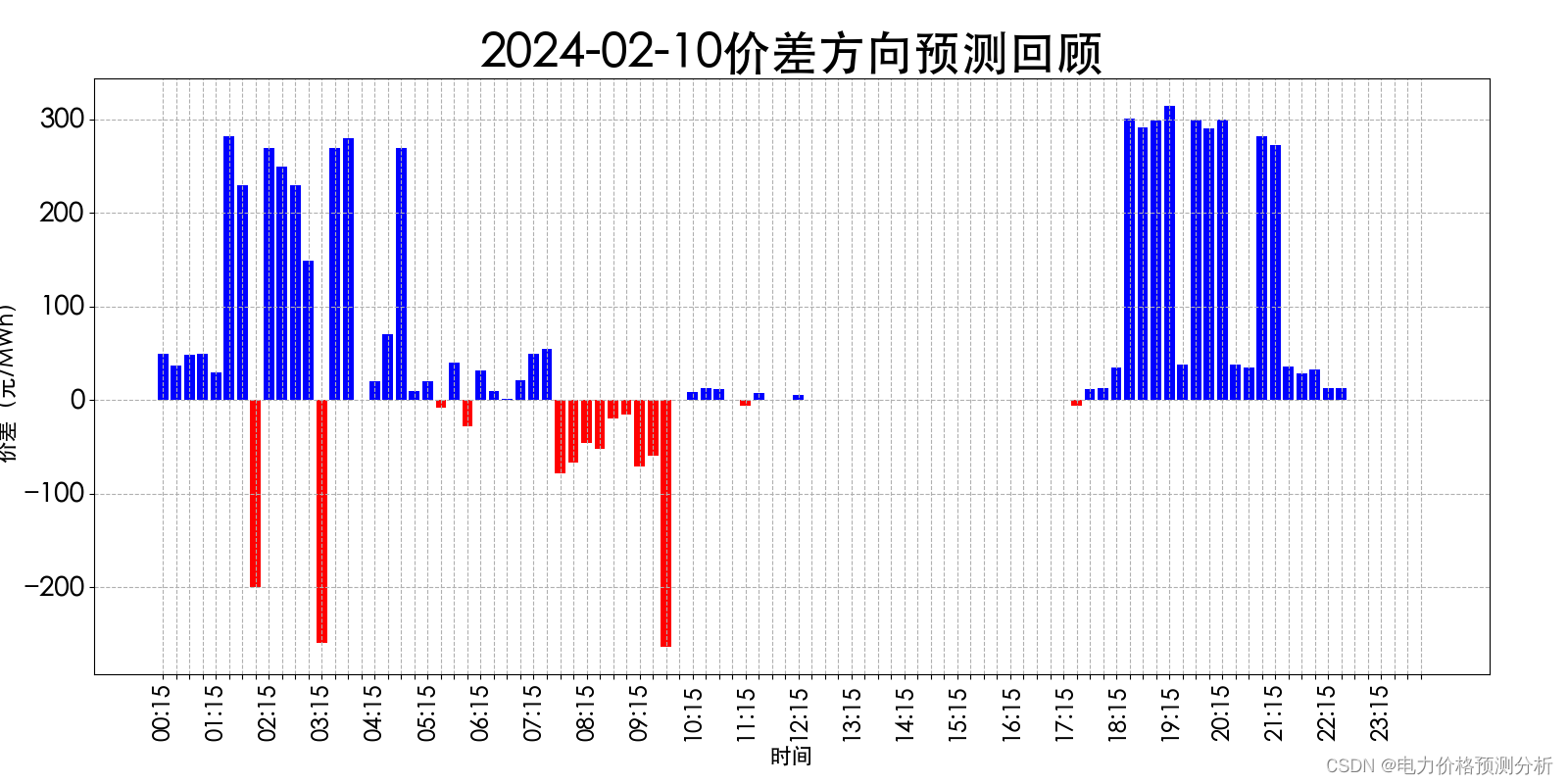
- 洛伦兹吸引子
- 仿真
简介
CellML是主打计算生理学的一个编程语言,擅长处理微分方程问题,并且内置了单位系统,是细胞层次的建模工具。openCOR为其运行环境,提供了舒适的代码编辑窗口,以及一系列IDE工具,包括查看内存,图形输出等。其官网地址为openCOR,下载相应的版本,安装之后,其界面如下

洛伦兹吸引子
洛伦兹吸引子即蝴蝶效应,是各种主打科学计算的编程语言都喜欢用作示例的一个模型,其数学模型是三个一阶常微分方程组(ODEs)
{ x ˙ = σ ( y − x ) y ˙ = x ( ρ − x ) − y z ˙ = x y − β z \left\{\begin{aligned} \dot x&=\sigma(y-x)\\ \dot y&=x(\rho-x)-y\\ \dot z&=xy-\beta z \end{aligned}\right. ⎩ ⎨ ⎧x˙y˙z˙=σ(y−x)=x(ρ−x)−y=xy−βz
这也是官方教程的一个示例,其参数设为
σ = 10 , ρ = 28 , β = 8 / 3 = 2.66667 \sigma=10, \rho=28, \beta=8/3=2.66667 σ=10,ρ=28,β=8/3=2.66667
初始条件为
x ( 0 ) = y ( 0 ) = z ( 0 ) = 1 x(0)=y(0)=z(0)=1 x(0)=y(0)=z(0)=1
下面将其写为CellML代码。点击【File】->【New】->【CellML File】,即可创建一个CellML文件,内容如下。
// CellML用//进行注释
def model Lorenz as
def comp main as
var t: dimensionless {init: 0};
var x: dimensionless {init: 1};
var y: dimensionless {init: 1};
var z: dimensionless {init: 1};
var sigma: dimensionless {init: 10};
var beta: dimensionless {init: 2.66667};
var rho: dimensionless {init: 28};
ode(x,t)=sigma*(y-x);
ode(y,t)=x*(rho-z)-y;
ode(z,t)=x*y-beta*z;
enddef;
enddef;
这几行代码的可读性非常强,首先定义一个模型lorenz,模型内部定义一个组件main,可以理解为入口函数。接下来 x , y , z , σ , β , ρ x,y,z,\sigma,\beta,\rho x,y,z,σ,β,ρ均为变量,最后是三个常微分方程,表示前文建立的模型。
当光标至于某行ode时,代码上方会出现其渲染的公式,非常便捷。

其选项卡标签File #2后面有个星星,说明当前文件未保存,可用【File】->【Save】或Ctrl+S将文件保存为cellml格式。
仿真
将代码输入框左侧的竖排选项卡,从【Editing】切换到【Simuliation】,其模拟结果如下。

其中,【Simulation】下拉框中存放的是仿真参数,为了能够清晰地展示 x , y , z x,y,z x,y,z之间的变化关系,将Ending Point设为50,Point interval设为0.01,二者分别表示终止时间和时间间隔。
点击左上角三角符号,即可完成仿真。点击下方【Parameters】下拉框,可实现二维图形的绘制。
目前尚未发现OpenCOR可以绘制三维图像,但可以将数据导出为csv文件。