洛谷P1934 封印

题目背景

很久以前，魔界大旱，水井全部干涸，温度也越来越高。为了拯救居民，夜叉族国王龙溟希望能打破神魔之井，进入人界“窃取”水灵珠，以修复大地水脉。可是六界之间皆有封印，神魔之井的封印由蜀山控制，并施有封印。龙溟作为魔界王族，习有穿行之术，可任意穿行至任何留有空隙的位置。然而封印不留有任何空隙！ 龙溟无奈之下只能强行破除封印。破除封印必然消耗一定的元气。为了寻找水灵珠，龙溟必须减少体力消耗。他可以在破除封印的同时使用越行术。

题目描述

神魔之井的封印共有 �n 层，每层封印都有一个坚固值。身为魔族的龙溟单独打破一层封印时需要消耗的元气为该层封印的坚固值和封印总层数 �n 的平方的乘积； 但他也可以打破第 i 层到第 j 层之间的所有封印( �<�i<j)，总元气消耗为第 �,�i,j 层封印的坚固值之和与第 �,�i,j 层之间所有封印层（包括第 �,�i,j 层）的坚固值之和的乘积，但为了不惊动蜀山，第 �,�i,j 层封印的坚固值之和不能大于 t （单独打破可以不遵守）。

输入格式

第一行包含两个正整数 n 和 t。
第二行有 n 个正整数，第 i 个数为 ai​，表示第 i 层封印的坚固值。

输出格式

仅一行，包含一个正整数，表示最小消耗元气。

输入输出样例

输入 #1复制

6 10
8 5 7 9 3 5

输出 #1复制

578

说明/提示

样例解释

先单独打破第一层，再用越行术从第二层直接打破到最后一层。 这样消耗元气 8×62+(5+5)×(5+7+9+3+5)=578

数据范围

对于 10%10% 的数据， n≤10；
对于 50%50% 的数据， n≤100；
对于 70%70% 的数据， n≤500；
对于 100%100% 的数据， n≤1000，ai​(1≤i≤n),t≤20000。

题目分析

1，据题意所以这题里面选择用dp来动态规划

2，创建一个dp数组dp[j]用来存放i层到截止到j层消耗的元气

3，由题目 "单独打破一层封印时需要消耗的元气为该层封印的坚固值和封印总层数 n 的平方的乘积".

"打破第 i 层到第 j 层封印(i<j)的总元气消耗为第 i, j 层封印的坚固值之和与第 i, j 层之间所有封印层（包括第 i, j 层）的坚固值之和的乘积。同时，为了不惊动蜀山，第 i, j 层封印的坚固值之和必须不大于一个固定值 t" 。

4，由此得出

1.  dp[j]=min(dp[j],dp[j-1]+a[j]*n*n);

 2.if(a[j]+a[i]<=t) dp[j]=min(dp[j],dp[i-1]+(a[j]+a[i])*(f[j]-f[i-1]));

代码示例

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,t;
ll a[1006];
ll s[1006];
ll dp[1006];
int main(){
     cin>>n>>t;
     for(int j=1;j<=n;j++)
     {
         cin>>a[j];
         s[j]=s[j-1]+a[j];//前缀和
         dp[j]=LONG_LONG_MAX;//因为找小值所以初始值大点
     }
     for(int j=1;j<=n;j++)
      {dp[j]=min(dp[j],dp[j-1]+a[j]*n*n);//单独打破一层
         for(int i=1;i<j;i++)
           if(a[j]+a[i]<=t)//第 i, j 层封印的坚固值之和必须不大于一个固定值 t
            dp[j]=min(dp[j],dp[i-1]+(a[j]+a[i])*(s[j]-s[i-1]));//i到j层的法力比较

      }
        cout<<dp[n];






}

洛谷P3375 【模板】KMP

题目描述

给出两个字符串 s1​ 和 s2​，若 s1​ 的区间 [l,r] 子串与 s2​ 完全相同，则称 s2​ 在 s1​ 中出现了，其出现位置为 l。
现在请你求出 s2​ 在 s1​ 中所有出现的位置。

定义一个字符串 s 的 border 为 s 的一个非 s 本身的子串 t，满足 t 既是 s 的前缀，又是 s 的后缀。
对于 s2​，你还需要求出对于其每个前缀 ′s′ 的最长 border ′t′ 的长度。

输入格式

第一行为一个字符串，即为 s1​。
第二行为一个字符串，即为 s2​。

输出格式

首先输出若干行，每行一个整数，按从小到大的顺序输出 s2​ 在 s1​ 中出现的位置。
最后一行输出 ∣s2​∣ 个整数，第 i 个整数表示 s2​ 的长度为 i 的前缀的最长 border 长度。

输入输出样例

输入 #1复制

ABABABC
ABA

输出 #1复制

1
3
0 0 1 

说明/提示

样例 1 解释

。

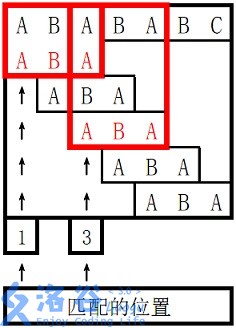
对于 s2​ 长度为 3的前缀 ABA，字符串 A 既是其后缀也是其前缀，且是最长的，因此最长 border 长度为 1。

数据规模与约定

本题采用多测试点捆绑测试，共有 3 个子任务。

• Subtask 1（30 points）：s1​∣≤15，s2​∣≤5。
• Subtask 2（40 points）：2∣≤102∣s2​∣≤102。
• Subtask 3（30 points）：无特殊约定。

对于全部的测试点，保证 1≤∣s1​∣,∣s2​∣≤106，s1​,s2​ 中均只含大写英文字母。

题目分析

1，这题属于一个经典的kmp模板题

2，

KMP算法是一种用于字符串匹配的经典算法，它的基本思想是利用已经匹配过的部分信息来减少不必要的比较次数，从而提高匹配的效率。

KMP算法的核心是构建一个部分匹配表（也称为next数组），这个表记录了在匹配过程中出现不匹配时，可以跳过已经匹配过的部分，从而减少比较次数。通过这个部分匹配表，KMP算法可以在不回溯的情况下，快速地找到匹配失败时需要移动的位置。

具体来说，KMP算法在匹配过程中，当发现不匹配时，会根据部分匹配表中的信息，将模式串向后移动一定的位置，而不是从头开始重新比较。这样就能够减少比较次数，提高匹配效率。

3，这算法主要的实现是next数组的创建

KMP算法中的next数组是用来存储模式串中每个位置的最长公共前缀和最长公共后缀的长度的数组。这个数组在KMP算法中用于在匹配过程中进行跳转，以避免不必要的比较。 具体来说，对于模式串P，next[i]表示P[0:i]这个子串的最长公共前缀和最长公共后缀的长度（不包括P[i]本身）。在KMP算法中，当P[i]和T[j]不匹配时（T为文本串），根据next数组的值可以快速地移动模式串，跳过已经匹配过的部分，从而提高匹配的效率。

假设我们有一个文本串 "ABC ABCDAB ABCDABCDABDE" 和一个模式串 "ABCDABD"。

首先，我们需要构建模式串 "ABCDABD" 的 next 数组。这个过程可以通过遍历模式串来完成，具体过程如下：

1. 首先，next[0] 总是 -1。
2. 然后，我们从第二个字符开始，依次计算每个位置的最长相同前缀后缀的长度。
   • next[1] = 0，因为第一个字符没有前缀和后缀。
   • next[2] = 0，因为 "AB" 的前缀和后缀没有重叠。
   • next[3] = 0，因为 "ABC" 的前缀和后缀没有重叠。
   • next[4] = 0，因为 "ABCD" 的前缀和后缀没有重叠。
   • next[5] = 1，因为 "ABCDA" 的前缀 "A" 和后缀 "A" 相同，长度为 1。
   • next[6] = 2，因为 "ABCDAB" 的前缀 "AB" 和后缀 "AB" 相同，长度为 2。
   • next[7] = 0，因为 "ABCDABD" 的前缀和后缀没有重叠。

因此，模式串 "ABCDABD" 的 next 数组为 [-1, 0, 0, 0, 0, 1, 2]。

接下来，我们使用KMP算法来在文本串中查找模式串。具体过程如下：

1. 我们将模式串 "ABCDABD" 和文本串 "ABC ABCDAB ABCDABCDABDE" 对齐，从头开始逐个字符进行比较。
2. 当模式串和文本串中的字符匹配时，继续比较下一个字符。
3. 当模式串和文本串中的字符不匹配时，根据 next 数组的值来移动模式串，而不是每次只移动一位。

 代码示例

#include<bits/stdc++.h>
using namespace std;
#define MAXnext 1000010
long long next1[MAXnext];
long long ls,ls1;
char s[MAXnext];
char s1[MAXnext];
void getnext(char a[])//创建next数组统计最长公共前缀长度
{
    long long j=0;
    for(long long i=1; i<ls1; i++)
    {
        while(a[i]!=a[j]&&j>0)
        {
            j=next1[j-1];
        }
        if(a[i]==a[j])j++;
        next1[i]=j;
    }
}
int main()
{
    scanf("%s",s);
    scanf("%s",s1);
    ls=strlen(s);
    ls1=strlen(s1);
    getnext(s1);
    long long j=0;
    for(long long i=0; i<ls; i++)
    {
        while(j>0&&s[i]!=s1[j])j=next1[j-1];//不相等就回到对应next数组前一位的位置
        if(s[i]==s1[j])j++;//相等就接着比较
        if(j==ls1)
           { printf("%lld\n",i-ls1+2);

           }
    }

    for(int i=0; i<ls1; i++)
  printf("%lld ",next1[i]);


}