目录
二分查找算法介绍
二分查找算法的简单应用
二分查找算法介绍
二分查找算法,指在一组有序的数组内查找数值,查找的数值与查找范围内的中间数值进行比较,如果比中间数值小,则在原范围内的左侧范围内重复与该范围内的中间数值比较;如果比中间数值大,则在原范围内的右侧范围内重复与该范围内的中间数值比较。以此类推,直到找到数值为止
//严格递增的数组
int arr[10] = { 1,5,9,10,15,20,21,30,35,45 };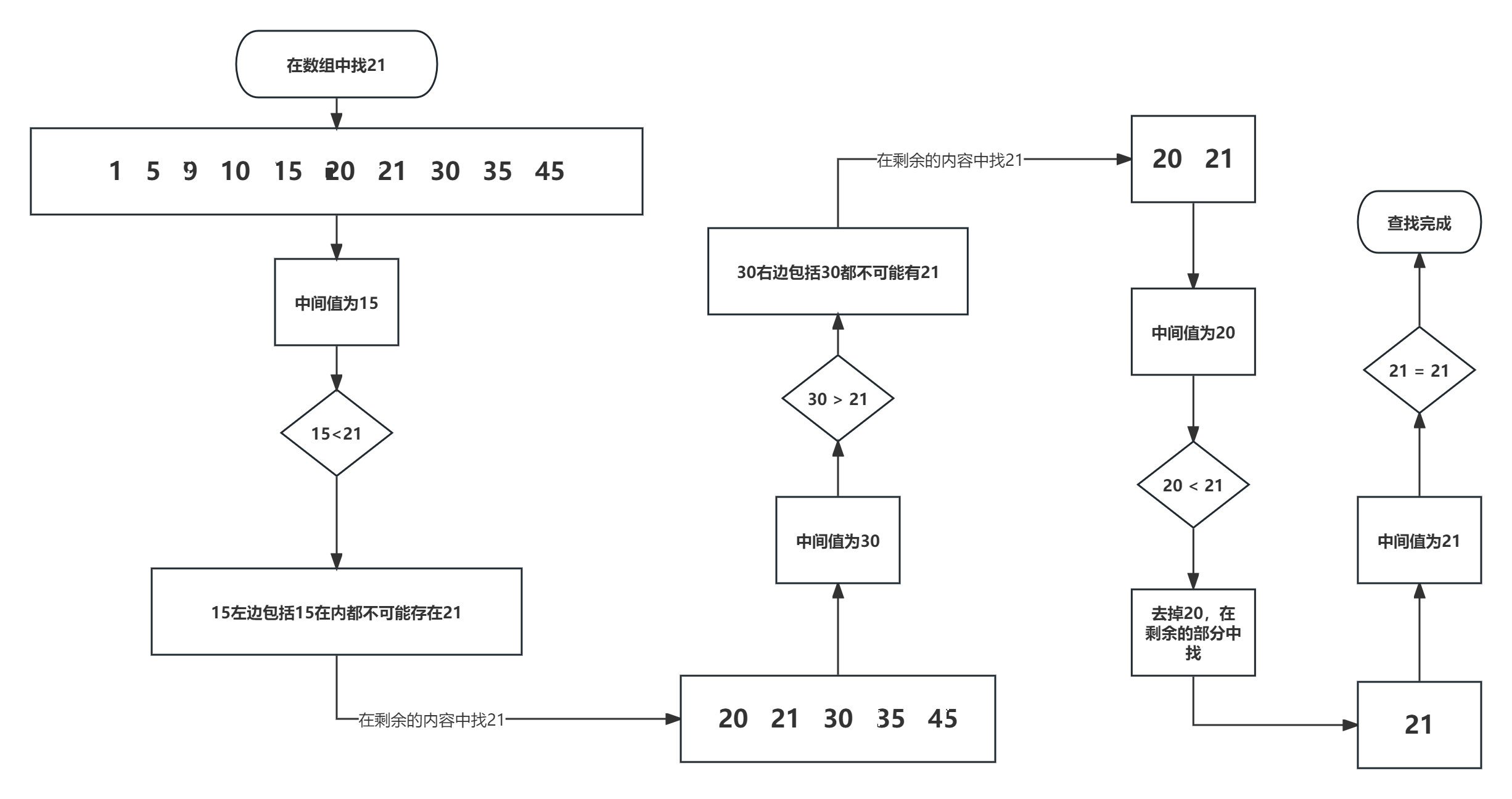
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
void binarySearch(int* nums, int numslen, int findNum)
{
//定义指向数组头和尾的两个变量
int left = 0;
int right = numslen - 1;
while (left <= right)//交叉时才停止,因为当两个指针都指向一个位置时,则中间值下标即为left或者right
{
//定义中间位置的变量
int mid = (left + right) / 2;
if (nums[mid] > findNum)
{
//当中间值大于需要查找的数值时,则需要查找的数值在中间值的左侧
//使右侧指针位于中间值下标的前一个下标位置
right = mid - 1;
}
else if(nums[mid] < findNum)
{
//当中间值小于需要查找的数值时,则需要查找的数值在中间值的右侧
//使左侧指针位于中间值下标的后一个位置
left = mid + 1;
}
else
{
//恰好时中间值时,直接返回
printf("找到数值,下标为%d", mid);
return;
}
}
if (left > right)
{
printf("无此数值");
}
}
int main()
{
int arr[10] = { 1,5,9,10,15,20,21,30,35,45 };
int sz = sizeof(arr) / sizeof(int);
binarySearch(arr, sz, 45);
return 0;
}
输入:
21
输出结果:
找到数值,下标为6二分查找算法的简单应用
在旋转后数组中查找数组的最小值
题目链接:旋转数组的最小数字_牛客题霸_牛客网
描述
有一个长度为 n 的非降序数组,比如[1,2,3,4,5],将它进行旋转,即把一个数组最开始的若干个元素搬到数组的末尾,变成一个旋转数组,比如变成了[3,4,5,1,2],或者[4,5,1,2,3]这样的。请问,给定这样一个旋转数组,求数组中的最小值。
数据范围:1≤ n≤10000,数组中任意元素的值: 0≤ val≤10000
要求:空间复杂度: O(1) ,时间复杂度: O()
思路分析:
因为原数组是一个非降序(即非严格递增)的数组,所以旋转后的数组将被分为两个有序的数组,对于二分查找来说,只需要查找的数组是有序即可,对于本题,因为存在两个有序的部分,故需要分别进行判断,确定好边界后缩小范围再进行二分查找,故本题有三种情况
1. 范围内的中间数值比右侧范围中的数值大。此时说明,数组中的最小数值在中间值的右侧,此时运用二分查找算法的思想,在右侧的部分中找最小值
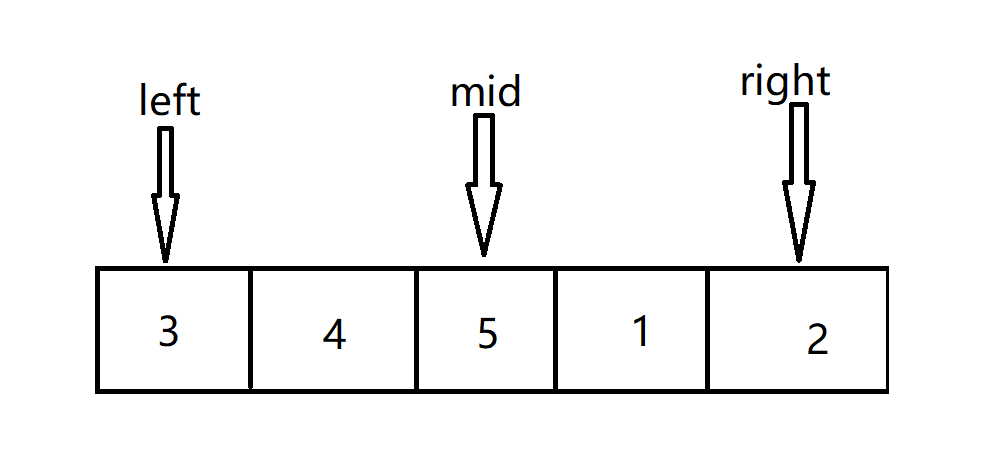
2. 范围内的中间数值比右侧范围中的数值小。此时说明,数组中的最小数值在中间值的左侧,此时运用二分查找算法的思想,在左侧的部分中找最小值

3. 范围内的中间数值和右侧范围中的数值相等。此时无法判断数组中的最小数值在哪一侧,此时逐渐缩小区间,重复判断直到出现上面两种情况中的一种再执行上面的两种情况的处理方法

/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param nums int整型一维数组
* @param numsLen int nums数组长度
* @return int整型
*/
int minNumberInRotateArray(int* nums, int numsLen ) {
int left = 0;
int right = numsLen - 1;
while(left <= right)
{
//指向中间位置的变量
int mid = (left + right) / 2;
if(nums[mid] > nums[right])
{
//当中间值大于右侧的值
//注意此处是left = mid + 1,left用于和right确定边界,当需要缩小范围时,mid位置的数值可以不再包括在内,因为当前数值已经比nums[right]大
left = mid + 1;
}
else if(nums[mid] < nums[right])
{
//当中间值小于右侧的值
//注意此处不是right = mid - 1,因为要与nums[right]进行比较从而确定边界,可能mid位置就是一侧边界
right = mid;
}
else {
//当中间值等于右侧的值
right--;
}
}
return nums[left];
}