Map和Set（哈希表）

map：

map说明：

Map.Entry的说明：,v>

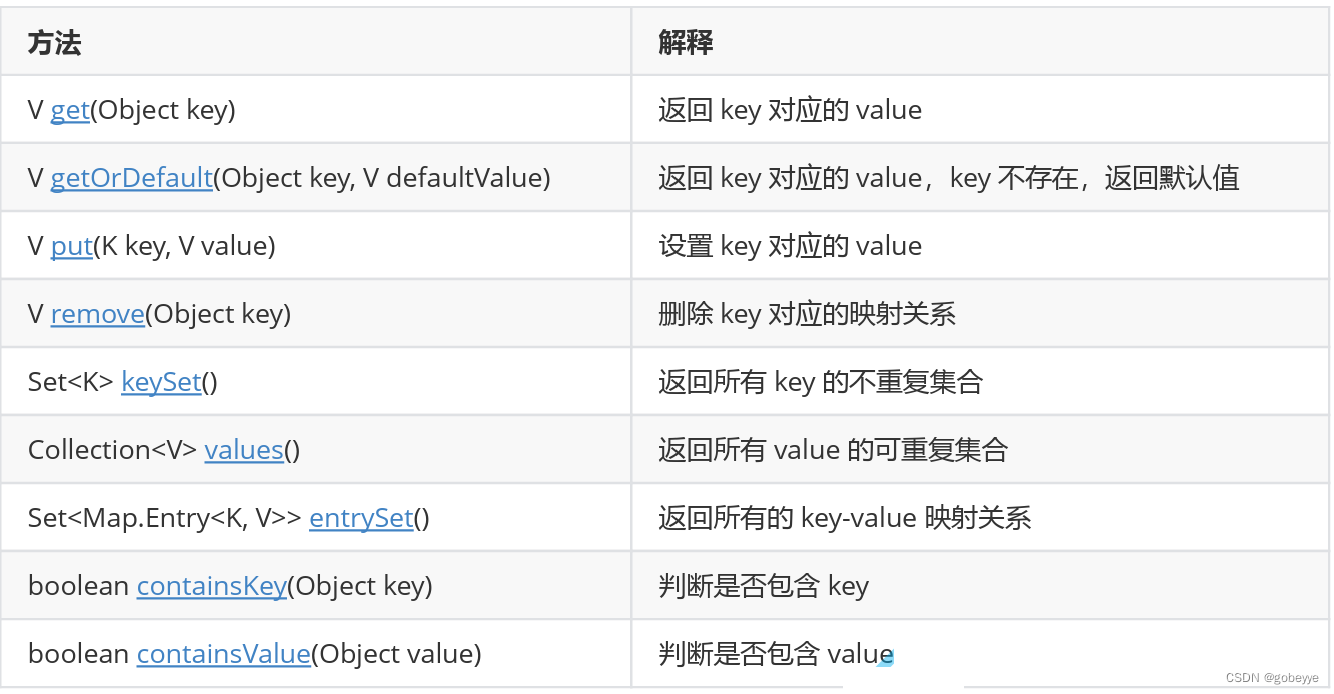
Map 的常用方法:

演示：

注意：

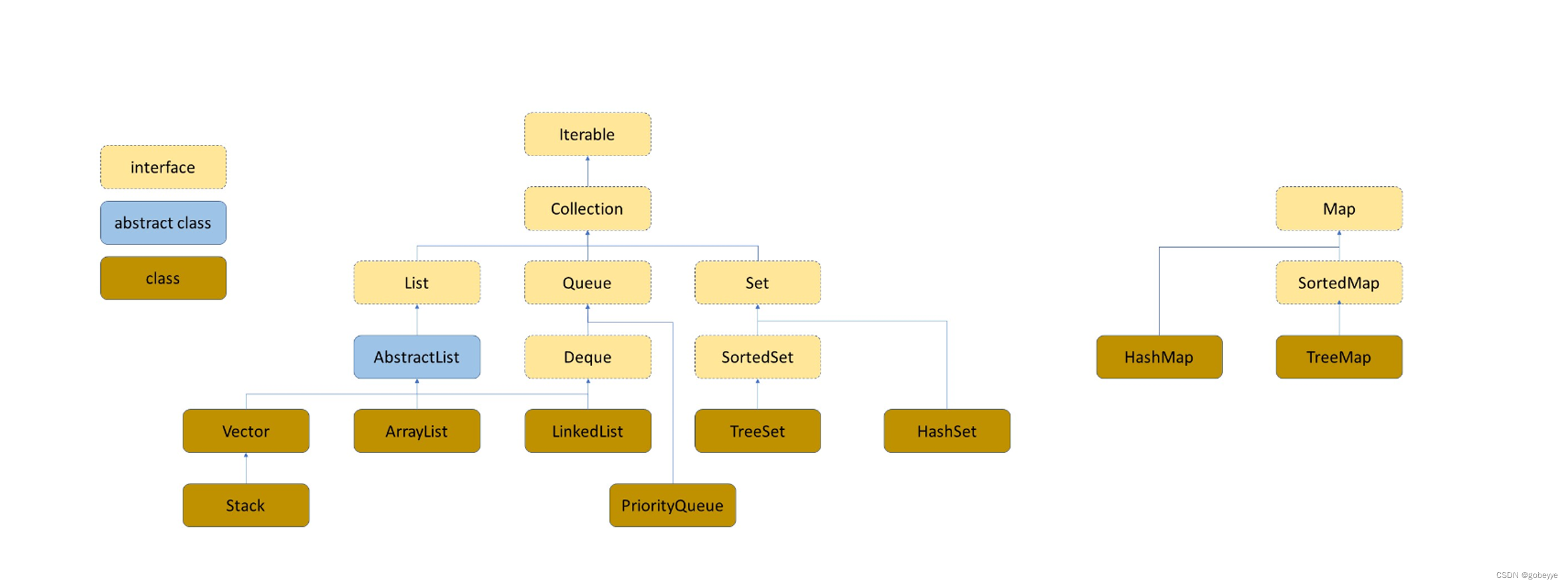
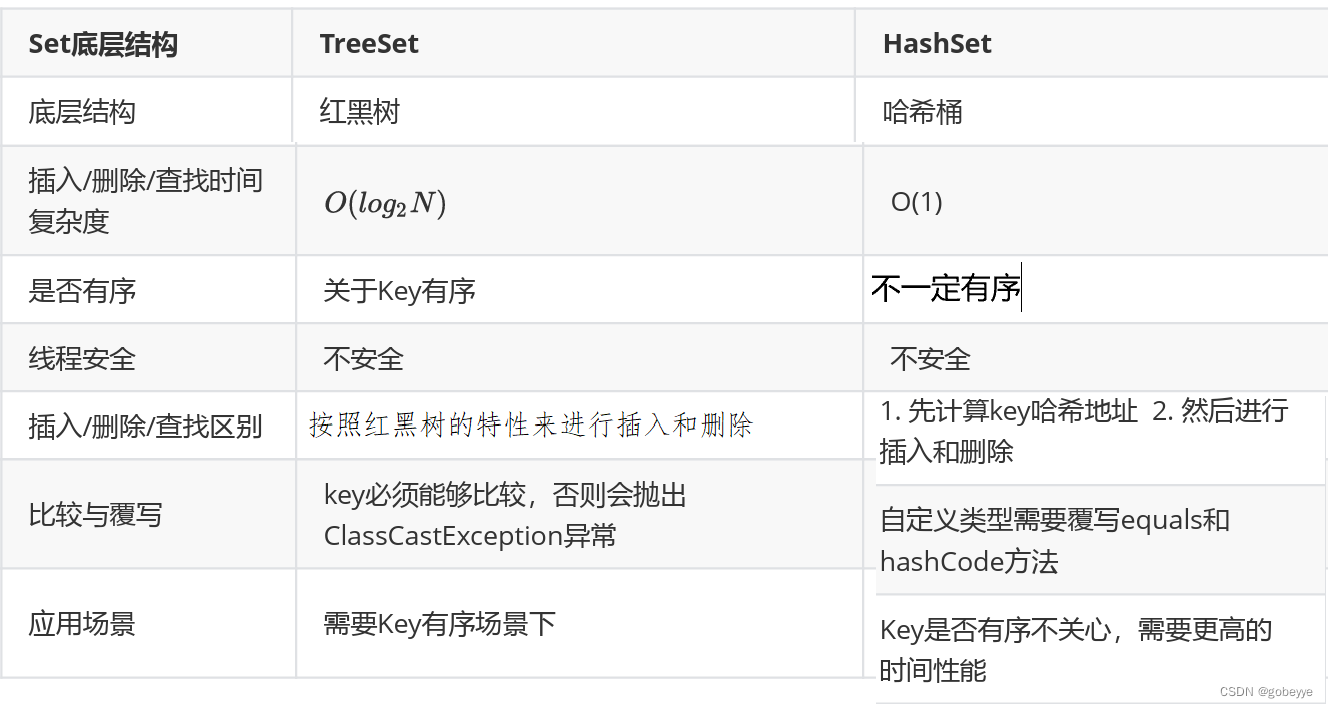
TreeMap和HashMap的区别

Set：

常见方法说明：

注意：

TreeSet和HashSet的区别

哈希表:

冲突：

冲突-避免：

冲突-避免-负载因子调节：

冲突-解决：

冲突-解决-闭散列：

冲突-解决-开散列/哈希桶：

结语：

map：

map说明：

Map是一个接口类，该类没有继承自Collection，该类中存储的是结构的键值对，并且K一定是唯一的，不能重复。

Map.Entry<K,V>的说明：

Map.Entry<K,V>是Map内部实现的用来存放键值对映射关系的内部类，该内部类中主要提供了<key,value> 的获取，value的设置以及Key的比较方式。

方法	解释
K getKey()	返回 entry 中的 key
V getValue()	返回 entry 中的 value
V setValue(V value)	将键值对中的value替换为指定value

注意：Map.Entry并没有提供设置Key的方法.

Map 的常用方法:

如下图所示：

Map底层可以用Hashmap和Treemap实现，由于Hashmap的效率比较高故下面我用Hashmap来进行演示。

演示：

import java.util.Map;
import java.util.HashMap;
import java.util.Set;
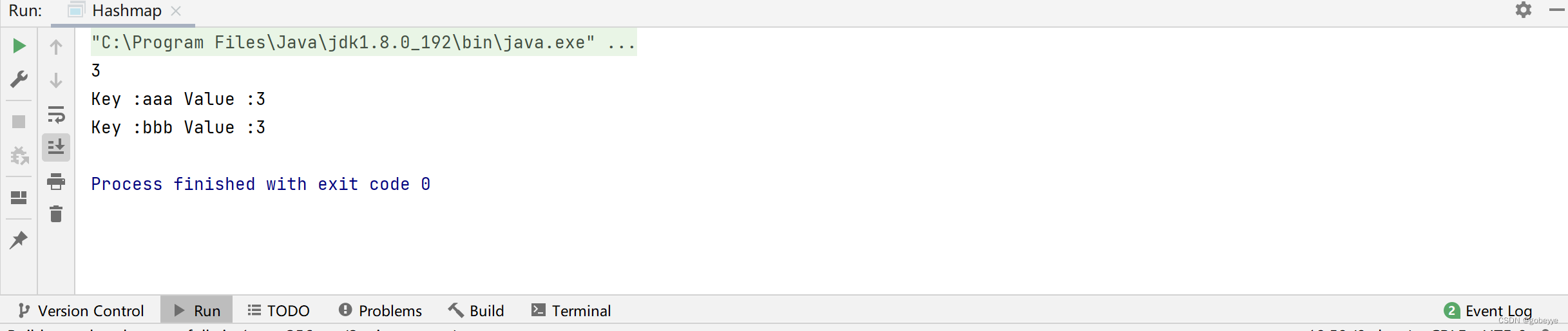
public class Hashmap {
    public static void main(String[] args) {
        Map<String,Integer> map = new HashMap<>();
        map.put("aaa",3);
        map.put("bbb",3);
        System.out.println(map.get("aaa"));
        Set<Map.Entry<String,Integer>> set = map.entrySet();
        for(Map.Entry<String,Integer> entry:set){
            System.out.println("Key :"+entry.getKey() + " Value :" + entry.getValue());
        }
    }
}

entrySet是比较重要的故进行演示。

效果如下：

这里采用foreach进行遍历，可以不用直到Set的长度。

注意：

1. Map是一个接口，不能直接实例化对象，如果要实例化对象只能实例化其实现类TreeMap或者HashMap。

2. Map中存放键值对的Key是唯一的，value是可以重复的。

3. 在TreeMap中插入键值对时，key不能为空，否则就会抛NullPointerException异常，value可以为空。但是HashMap的key和value都可以为空。

4. Map中的Key可以全部分离出来，存储到Set中来进行访问(因为Key不能重复)。

5. Map中的value可以全部分离出来，存储在Collection的任何一个子集合中(value可能有重复)。

6. Map中键值对的Key不能直接修改，value可以修改，如果要修改key，只能先将该key删除掉，然后再来进行重新插入。

TreeMap和HashMap的区别

Set：

Set与Map主要的不同有两点：Set是继承自Collection的接口类，Set中只存储了Key。

常见方法说明：

方法	解释
boolean add(E e）	添加元素，但重复元素不会被添加成功
void clear(）	清空集合
boolean contains(Object o）	判断 o 是否在集合中
Iterator iterator(）	返回迭代器
boolean remove(Object o)	删除集合中的 o
int size(）	返回set中元素的个数
boolean isEmpty(）	检测set是否为空，空返回true，否则返回false
Object[] toArray(）	将set中的元素转换为数组返回
boolean containsAll(Collection c）	集合c中的元素是否在set中全部存在，是返回true，否则返回 false
boolean addAll(Collection c）	将集合c中的元素添加到set中，可以达到去重的效果

演示：

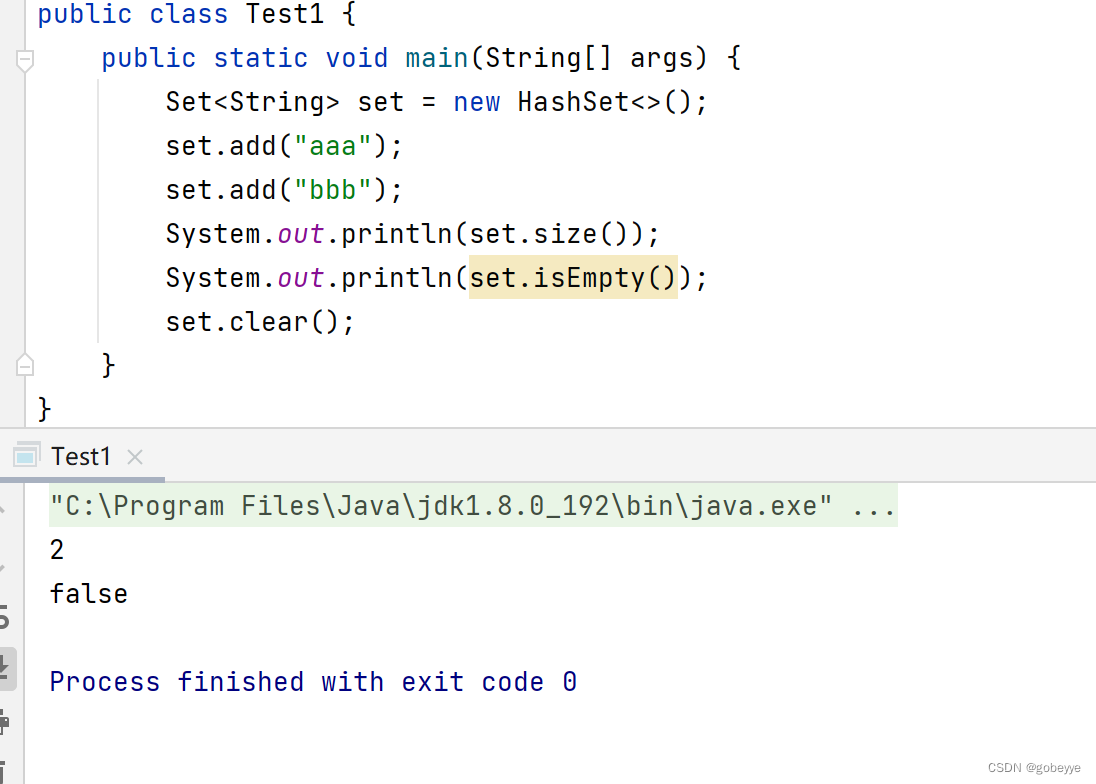
public class Test1 {
    public static void main(String[] args) {
        Set<String> set = new HashSet<>();
        set.add("aaa");
        set.add("bbb");
        System.out.println(set.size());
        System.out.println(set.isEmpty());
        set.clear();
    }
}

效果如下：

注意：

1. Set是继承自Collection的一个接口类。

2. Set中只存储了key，并且要求key一定要唯一。

3. TreeSet的底层是使用Map来实现的，其使用key与Object的一个默认对象作为键值对插入到Map中的。

4. Set最大的功能就是对集合中的元素进行去重。

5. 实现Set接口的常用类有TreeSet和HashSet，还有一个LinkedHashSet，LinkedHashSet是在HashSet的基础上维护了一个双向链表来记录元素的插入次序。

6. Set中的Key不能修改，如果要修改，先将原来的删除掉，然后再重新插入。

7. TreeSet中不能插入null的key，HashSet可以。

TreeSet和HashSet的区别

哈希表:

概念：

顺序结构以及平衡树中，元素关键码与其存储位置之间没有对应的关系，因此在查找一个元素时，必须要经过关键码的多次比较。顺序查找时间复杂度为O(N)，平衡树中为树的高度，即O(logn )，搜索的效率取决于搜索过程中元素的比较次数。

理想的搜索方法：可以不经过任何比较，一次直接从表中得到要搜索的元素。如果构造一种存储结构，通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系，那么在查找时通过该函数可以很快找到该元素。

插入元素：

根据待插入元素的关键码，以此函数计算出该元素的存储位置并按此位置进行存放。

搜索元素：

对元素的关键码进行同样的计算，把求得的函数值当做元素的存储位置，在结构中按此位置取元素比较，若关键码相等，则搜索成功。

该方式即为哈希(散列)方法，哈希方法中使用的转换函数称为哈希(散列)函数，构造出来的结构称为哈希表(Hash Table)(或者称散列表)

冲突：

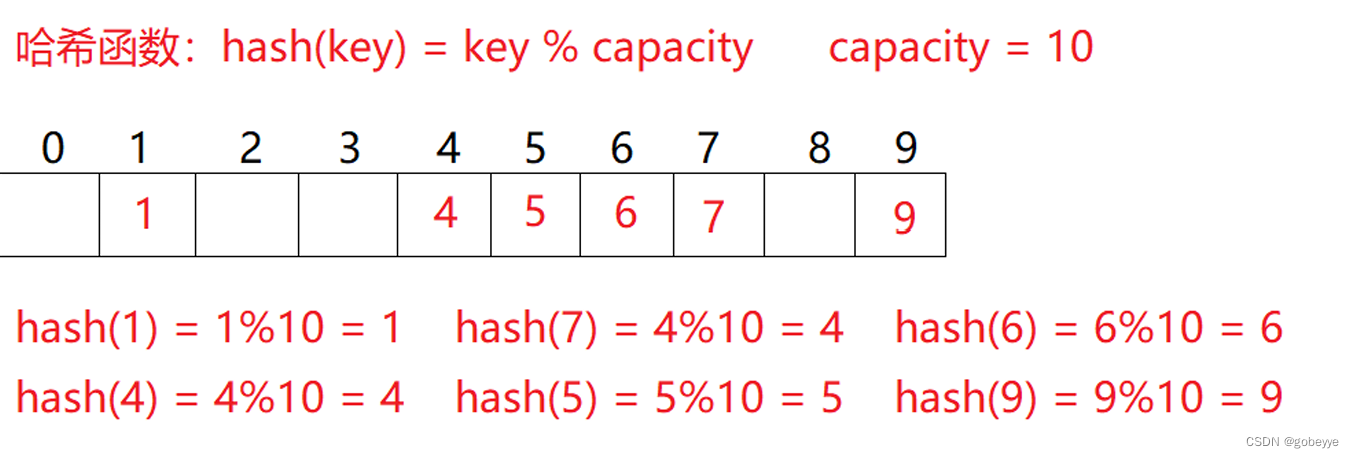
对于两个数据元素的关键字和 (i != j)，有 != ，但有：Hash( ) == Hash( )，即：不同关键字通过相同哈希哈数计算出相同的哈希地址，该种现象称为哈希冲突或哈希碰撞。把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。

例如：

下图的4和7就是发生了冲突。

冲突-避免：

首先，我们需要明确一点，由于我们哈希表底层数组的容量往往是小于实际要存储的关键字的数量的，这就导致一个问题，冲突的发生是必然的，但我们能做的应该是尽量的降低冲突率。

函数设计：

哈希函数设计原则：

（1）哈希函数的定义域必须包括需要存储的全部关键码，而如果散列表允许有m个地址时，其值域必须在0到m-1 之间。

（2）哈希函数计算出来的地址能均匀分布在整个空间中。

（3）哈希函数应该比较简单。

常见哈希函数：

（1）直接定制法：

取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B 优点：简单、均匀缺点：需要事先知道关键字的分布情况使用场景：适合查找比较小且连续的情况。

（2）除留余数法：

设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，按照哈希函数： Hash(key) = key% p(p<=m),将关键码转换成哈希地址。

冲突-避免-负载因子调节：

已知哈希表中已有的关键字个数是不可变的，那我们能调整的就只有哈希表中的数组的大小。

冲突-解决：

解决哈希冲突两种常见的方法是：闭散列和开散列。

冲突-解决-闭散列：

闭散列：也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以把key存放到冲突位置中的“下一个” 空位置中去。

寻找方法：

（1）线性探测

线性探测：从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止。

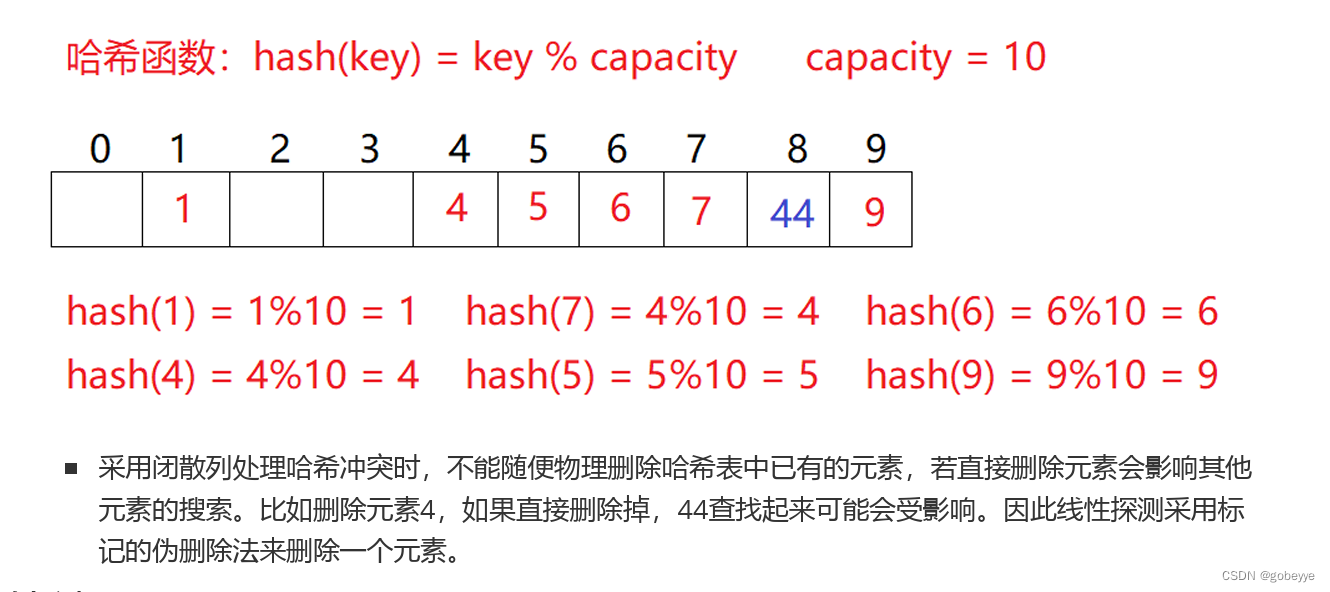
注意：这里的删除都是伪删除。

（2）二次探测：

找下一个空位置的方法为： = ( + )% m, 或者： = ( - )% m。其中：i = 1,2,3…，是通过散列函数Hash(x)对元素的关键码 key 进行计算得到的位置， m是表的大小。

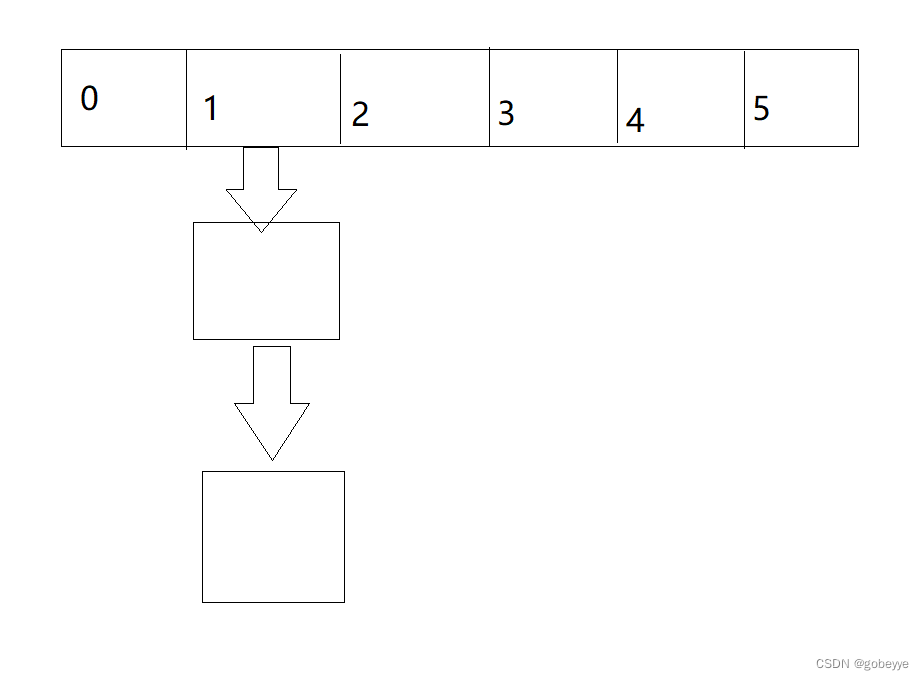
冲突-解决-开散列/哈希桶：

开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中。

简单来说就是数组加链表。

如图：

开散列，可以认为是把一个在大集合中的搜索问题转化为在小集合中做搜索了。

源代码的实现：


public class HashBucket {
    static class Node{
        private int key;
        private int value;
        Node next;
        public Node(int key,int value){
            this.key = key;
            this.value = value;
        }
    }
    private Node[] array;
    private int size;
    public HashBucket(){
        array = new Node[8];
        size = 0;
    }
    private static final double LOAD_FACTOR = 0.75;
    public int put(int key,int value){
        int index = key % array.length;
        Node cur = array[index];
        for(;cur != null; cur = cur.next){
            if(cur.key == key){
                int oldValue = cur.value;
                cur.value = value;
                return oldValue;
            }
        }
        Node node = new Node(key,value);
        node.next = array[index];
        array[index] = node;
        size++;
        if(loadFactor() >= LOAD_FACTOR){
            resize();
        }
        return -1;
    }
    //重新哈希
    private void resize(){
        Node[] newArray = new Node[array.length * 2];
        for(int i = 0;i < array.length; i++){
            Node next;
            for(Node cur = array[i]; cur != null; cur = next){
                next = cur.next;
                int index = cur.key % newArray.length;
                cur.next = newArray[index];
                newArray[index] = cur;
            }
        }
        array = newArray;
    }
    private double loadFactor(){
        return size * 1.0 / array.length;
    }
    public int get(int key){
        int index = key % array.length;
        for(Node cur = array[index]; cur != null; cur = cur.next){
            if(key == cur.key){
                return cur.value;
            }
        }
        return -1;
    }

}

性能分析：

虽然哈希表一直在和冲突做斗争，但在实际使用过程中，我们认为哈希表的冲突率是不高的，冲突个数是可控的，也就是每个桶中的链表的长度是一个常数，所以，通常意义下，我们认为哈希表的插入/删除/查找时间复杂度是 O(1) 。