二叉树进阶
- 一.二叉搜索树:
- 1.二叉搜索树的概念:
- 2.二叉搜索树的实现---循环版本:
- 1.二叉搜索树的基本结构:
- 2.查找:
- 3.插入:
- 4.中序遍历:
- 5.删除:
- 3.二叉搜索树的实现---递归版本:
- 1.查找
- 2.插入
- 3.删除:
- 4.拷贝构造和赋值构造:
- 1.拷贝构造:
- 2.赋值:
- 3.析构函数:
- 5.二叉搜索树的应用(Key-value模型):
- 1.字典:
- 2.小区和商场停车位。
- 二.二叉树的笔试题目:
- 1.根据二叉树创建字符串
- 思路一
- 2.二叉树的层序遍历(二)
- 思路一
- 3.二叉树的最近公共祖先:
- 思路一:
- 思路二:
- GIF题目解析
- 4.二叉搜索树与双向链表:
- 思路一
一.二叉搜索树:
1.二叉搜索树的概念:
为什么要有二叉搜索树:因为之前进行数据的查找一般是进行排序+二分,如果要插入删除数据是比较麻烦的,有序的数组不好去维持。
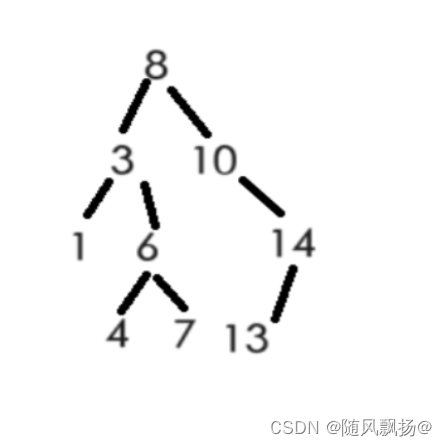
1.二叉搜索树可以是一个空树:
2.二叉搜索树的根节点的值大于左子树中的所有节点。
3.二叉搜索树的根节点的值小于右子树中的所有节点。
4.二叉搜索树中没有重复的值节点。
5.左右子树满足二叉搜索树的要求。
2.二叉搜索树的实现—循环版本:
特点:
1.二叉搜索树又叫二叉排序树,因为二叉搜索树的中序遍历是一个升序。
2.二叉搜索树这个结构的插入删除查找的效率都比较不错
1.二叉搜索树的基本结构:
template<class T>
struct TreeNode {
TreeNode(const T& x)
:_date(x)
,left(nullptr)
,right(nullptr)
{}
T _date;
TreeNode* left;
TreeNode* right;
};
2.查找:
1.二叉搜索树只去保存一个根节点。
2.当二叉搜索树的根节点为空说明当前是一个空树。
3.当二叉搜索树的根节点不为空说明当前不是一个空树。
4.根据需要查找的值和当前节点的大小关系进行迭代遍历。
5.查找的值比当前节点的值小,查找的值比当前节点的值大,查找的值和当前的值相等(说明找到节点)。
template<class T>
class BSTree {
typedef TreeNode<T> Node;
typedef Node* Proot;
public:
Proot find(T x)
{
//相等,x值大,x值小。
if (_root == nullptr)
return nullptr;
Proot root = _root;
while (root!=nullptr)
{
if (x < root->_date)
{
root = root->left;
}
else if (x > root->_date)
{
root = root->right;
}
else
{
return root;
}
}
return nullptr;
}
private:
Proot _root=nullptr;
};
3.插入:
1,每次插入是需要创建新的节点的。
2.如果当前二叉树为空直接修改_root.
3.当前二叉树中有数据的话需要先去找数据。
4.注意一个问题:进行连接的时候是需要前面一个节点的遍历找到nullptr说明这个空可以被插入,需要判断大小需要再一次判断,判断空需要再一次判断。
5.如果存在数值相等的情况需要直接返回这个值插入不了。
bool insert(T x)
{
//1.当前二叉树中没有元素:
if (_root == nullptr)
{
Proot newnode = new TreeNode<T>(x);
_root = newnode;
}
//2.当前二叉树中有元素:
else
{
Proot newnode = new TreeNode<T>(x);
Proot root = _root;
Proot prev = _root;
while (root != nullptr)
{
if (x < root->_date)
{
prev = root;
root = root->left;
}
else if (x > root->_date)
{
prev = root;
root = root->right;
}
else
return false;
}
if (x < prev->_date && prev->left == nullptr)
prev->left = newnode;
else
prev->right = newnode;
return true;
}
}
4.中序遍历:
1.获取中序遍历根节点的方法,多包一层进行递归(一般涉及到递归都使用这个方法)。
2.使用GetRoot函数在类外进行操作。
//3.中序遍历:
void _InOrder(Proot root)
{
if (root == nullptr)
return;
_InOrder(root->left);
cout << root->_date << " ";
_InOrder(root->right);
}
Proot GetRoot()
{
return _root;
}
void InOrder()
{
_InOrder(_root);
}
5.删除:
步骤一:
1.找到对应需要删除的节点指针。
2.使用find的思路并且保存cur节点的prev节点。
3.进入不同类型节点的删除分类:
删除节点的情况分类:
1.删除叶子节点:叶子节点无牵无挂,只需要让前面一个节点,指向这个节点的方向指向空就可以了。
2.删除有一个孩子的节点:一个孩子节点被删除我们需要拜托删除节点的父节点连接删除节点的子节点,我们需要去判断被删除的节点的孩子在删除节点的左还是删除节点的右。判断父节点的左还是右是需要删除的节点。
3.删除有两个孩子的节点:
替换法删除—>可以使用当前要被删除节点的左数的最大值进行值替换。
---->可以使用当前要被删除节点的右数的最小值进行值替换。
使用右数的最小值进行举例:右数的最小一定在右树的最左边,值替换之后,删除这个右数最小值节点,这个节点要么没有孩子要么只有一个右孩子情况比较清楚!
注意特殊情况:
1.找右子树的最左节点右子树的根节点就是。
循环版本:
bool erase(const T x)
{
if (_root == nullptr)
return false;
//1.找到节点:
Proot cur = _root;
Proot prev = _root;
while (cur != nullptr)
{
if (x < cur->_date)
{
prev = cur;
cur = cur->left;
}
else if (x > cur->_date)
{
prev = cur;
cur = cur->right;
}
else
{
//1.找到节点就需要删除节点:
if (cur->left == nullptr && cur->right == nullptr)
{
if (prev->left == cur)
prev->left = nullptr;
else if (prev->right == cur)
prev->right = nullptr;
else if (cur == _root)
{
delete cur;
_root = nullptr;
return true;
}
delete cur;
return true;
}
//1-1:只有一个孩子的时侯:
if (cur->left == nullptr)
{
if (prev->left == cur)
prev->left = cur->right;
else if(prev->right == cur)
prev->right = cur->right;
delete cur;
return true;
}
else if (cur->right == nullptr)
{
if (prev->left == cur)
prev->left = cur->left;
else if (prev->right == cur)
prev->right = cur->left;
delete cur;
return true;
}
//1-2:有两个孩子的时候:
else
{
//1.找右子树最左边的:
Proot right_min = cur->right;
Proot right_min_parent = nullptr;
while (right_min->left)
{
right_min_parent = right_min;
right_min = right_min->left;
}
//2.进行值替换:
cur->_date = right_min->_date;
if (right_min_parent == nullptr)
{
cur->right = right_min->right;
}
else
{
right_min_parent->left = right_min->right;
}
delete right_min;
return true;
}
}
}
}
3.二叉搜索树的实现—递归版本:
1.递归版本比较循环版本需要多去套一层函数。
2.在插入和删除的时候不需要去保存前一个节点只需要参数使用引用。
3.删除有两个孩子的节点的时候,使用循环找到右子树的最小值,进行值交换。
4.进入递归去找交换好数指的节点就可以进行叶子节点或者只有一个孩子的节点删除。
1.查找
T find_R(const T key)
{
Proot tmp = _find_R(_root , key);
return tmp->_date;
}
private:
Proot _find_R(Proot root , const T key)
{
if (root == nullptr)
return nullptr;
if (root->_date == key)
return root;
else if (root->_date < key)
return _find_R(root->right, key);
else if (root->_date > key)
return _find_R(root->left, key);
}
2.插入
bool Insert_R(const T key)
{
if (_root == nullptr)
{
_root = new TreeNode<T>(key);
return true;
}
Proot cur = _root;
return _Insert_R(cur, key);
}
private:
bool _Insert_R(Proot& cur, const T key)
{
//1.找到合适的位置了:
if (cur == nullptr)
{
Proot newnode = new TreeNode<T>(key);
cur = newnode;
return true;
}
if (cur->_date == key)
return false;
else if (cur->_date < key)
return _Insert_R(cur->right, key);
else if (cur->_date > key)
return _Insert_R(cur->left, key);
}
3.删除:
bool erase_R(const T key)
{
if (_root == nullptr)
return false;
if (_root->left == nullptr && _root->right == nullptr)
{
delete _root;
_root = nullptr;
return true;
}
Proot cur = _root;
return _erase_R(cur , key);
}
private:
bool _erase_R(Proot& cur , const T key)
{
if (cur == nullptr)
return false;
//找到节点:可以删除
if (cur->_date == key)
{
//1.保存删除的节点:
Proot del = cur;
//2.孩子的情况:
if (cur->left == nullptr && cur->right == nullptr)
{
cur = nullptr;
}
else if (cur->left == nullptr && cur->right != nullptr)
{
cur = cur->right;
}
else if (cur->left != nullptr && cur->right == nullptr)
{
cur = cur->left;
}
//3.有两个孩子:
else
{
Proot right_min = cur->right;
while (right_min->left)
{
right_min = right_min->left;
}
//2.进行值交换:
swap(right_min->_date, cur->_date);
return _erase_R(cur->right, key);
}
delete del;
return true;
}
else if (cur->_date < key)
{
return _erase_R(cur->right, key);
}
else if (cur->_date > key)
{
return _erase_R(cur->left, key);
}
return false;
}
4.拷贝构造和赋值构造:
1.拷贝构造:
//1.自己写了不会生成默认构造!
//2.我们还是希望生成默认构造的!
BSTree() = default;
BSTree(const BSTree<T>& t)
{
_root = copy(t._root);
}
Proot copy(Proot root)
{
if (root == nullptr)
return nullptr;
TreeNode<T>* newnode = new TreeNode<T>(root->_date);
newnode->left = copy(root->left);
newnode->right = copy(root->right);
return newnode;
}
2.赋值:
//赋值的现代写法:
BSTree<T>& operator=(BSTree<T> t)
{
swap(_root, t._root);
return *this;
}
3.析构函数:
//析构函数:
~BSTree()
{
destroy(_root);
}
void destroy(Proot root)
{
if (root == nullptr)
return;
destroy(root->left);
destroy(root->right);
delete root;
}
5.二叉搜索树的应用(Key-value模型):
1.字典:
int main()
{
key_value::BSTree<string,string> Tree;
string word;
Tree.insert("one", "一");
Tree.insert("two", "二");
Tree.insert("three", "三");
Tree.insert("four", "四");
Tree.insert("five", "五");
Tree.insert("six", "六");
Tree.insert("seven", "七");
Tree.insert("eight", "八");
while (cin >> word)
{
string chinese = Tree.find(word);
cout << chinese << endl;
}
return 0;
}
namespace key_value {
template<class T , class V>
struct TreeNode {
TreeNode(const T& x , const V& value)
:_date(x)
,_value(value)
,left(nullptr)
,right(nullptr)
{}
T _date;
V _value;
TreeNode* left;
TreeNode* right;
};
template<class T, class V>
class BSTree {
typedef TreeNode<T,V> Node;
typedef Node* Proot;
public:
//析构函数:
~BSTree()
{
destroy(_root);
}
void destroy(Proot root)
{
if (root == nullptr)
return;
destroy(root->left);
destroy(root->right);
delete root;
}
//1.自己写了不会生成默认构造!
//2.我们还是希望生成默认构造的!
BSTree() = default;
BSTree(const BSTree<T,V>& t)
{
_root = copy(t._root);
}
Proot copy(Proot root)
{
if (root == nullptr)
return nullptr;
TreeNode<T, V>* newnode = new TreeNode<T, V>(root->_date);
newnode->left = copy(root->left);
newnode->right = copy(root->right);
return newnode;
}
//赋值的现代写法:
BSTree<T,V>& operator=(BSTree<T,V> t)
{
swap(_root, t._root);
return *this;
}
//1.插入元素:
bool insert(T x , V value)
{
//1.当前二叉树中没有元素:
if (_root == nullptr)
{
Proot newnode = new TreeNode<T,V>(x,value);
_root = newnode;
}
//2.当前二叉树中有元素:
else
{
Proot newnode = new TreeNode<T, V>(x, value);
Proot root = _root;
Proot prev = _root;
while (root != nullptr)
{
if (x < root->_date)
{
prev = root;
root = root->left;
}
else if (x > root->_date)
{
prev = root;
root = root->right;
}
else
return false;
}
if (x < prev->_date && prev->left == nullptr)
prev->left = newnode;
else
prev->right = newnode;
return true;
}
}
//2.find函数:
V find(T x)
{
//相等,x值大,x值小。
if (_root == nullptr)
return "查无此项";
Proot root = _root;
while (root!=nullptr)
{
if (x < root->_date)
{
root = root->left;
}
else if (x > root->_date)
{
root = root->right;
}
else
{
return root->_value;
}
}
return "查无此项";
}
//3.中序遍历:
void _InOrder(Proot root)
{
if (root == nullptr)
return;
_InOrder(root->left);
cout << root->_date << " ";
_InOrder(root->right);
}
Proot GetRoot()
{
return _root;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
//4.删除元素:
bool erase(const T x)
{
if (_root == nullptr)
return false;
//1.找到节点:
Proot cur = _root;
Proot prev = _root;
while (cur != nullptr)
{
if (x < cur->_date)
{
prev = cur;
cur = cur->left;
}
else if (x > cur->_date)
{
prev = cur;
cur = cur->right;
}
else
{
//1.找到节点就需要删除节点:
if (cur->left == nullptr && cur->right == nullptr)
{
if (prev->left == cur)
prev->left = nullptr;
else if (prev->right == cur)
prev->right = nullptr;
else if (cur == _root)
{
delete cur;
_root = nullptr;
return true;
}
delete cur;
return true;
}
//1-1:只有一个孩子的时侯:
if (cur->left == nullptr)
{
if (prev->left == cur)
prev->left = cur->right;
else if(prev->right == cur)
prev->right = cur->right;
delete cur;
return true;
}
else if (cur->right == nullptr)
{
if (prev->left == cur)
prev->left = cur->left;
else if (prev->right == cur)
prev->right = cur->left;
delete cur;
return true;
}
//1-2:有两个孩子的时候:
else
{
//1.找右子树最左边的:
Proot right_min = cur->right;
Proot right_min_parent = nullptr;
while (right_min->left)
{
right_min_parent = right_min;
right_min = right_min->left;
}
//2.进行值替换:
cur->_date = right_min->_date;
cur->_value = right_min->_value;
if (right_min_parent == nullptr)
{
cur->right = right_min->right;
}
else
{
right_min_parent->left = right_min->right;
}
delete right_min;
return true;
}
}
}
}
private:
Proot _root=nullptr;
};
}
2.小区和商场停车位。
1,小区车牌号,车排号在数据库中抬杆。
2.商场的停车场,保存车牌号和停车时间出去的时候根据车牌号找到停车时间。
3.计算需要交的钱树和支付系统绑定进行轮询查询确定是否抬杆。
二.二叉树的笔试题目:
根据二叉树创建字符串
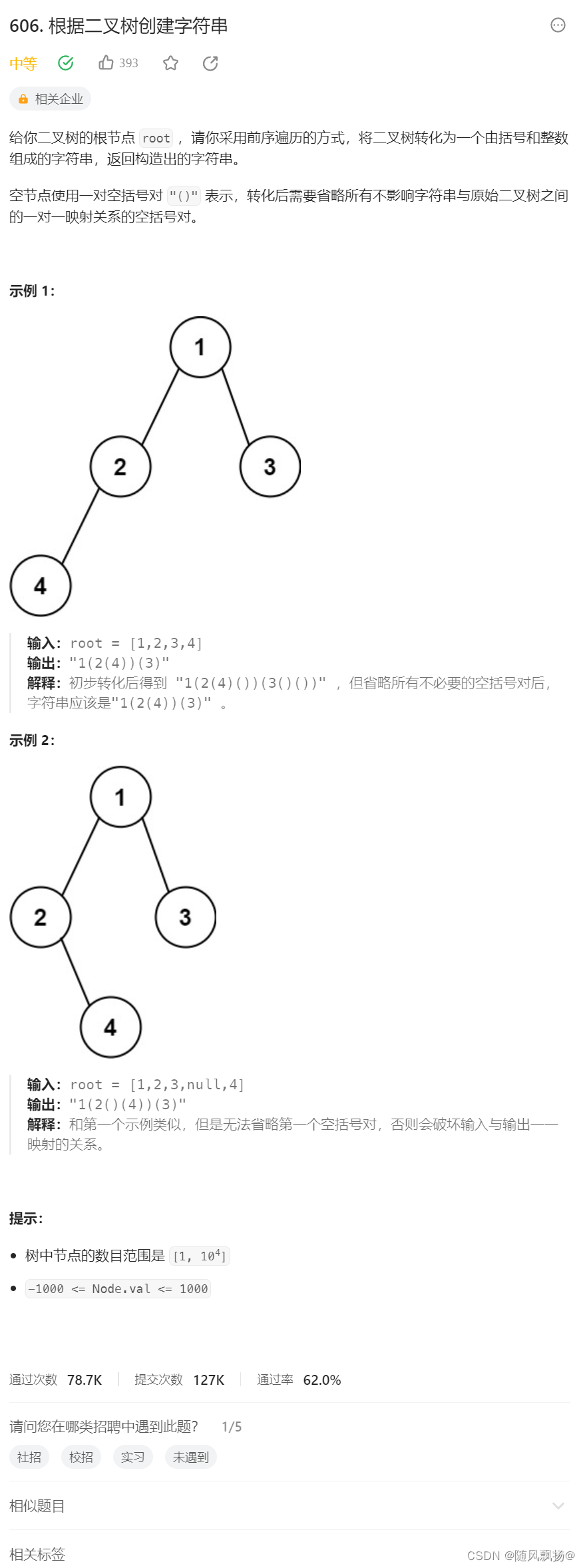
1.根据二叉树创建字符串
思路一
1.走一个前序遍历,使用一个引用参数去保存字符串。
2.尾插一个左括号,插入当前数据的字符串,进入左右子树,尾插右括号。
3.空节点使用()表示,左子树为空,右子数不为空,才需要()。
4.根节点数据不需要左右括号,开始的特殊判断不插入左括号最后还需要考虑一个尾删。
class Solution {
public:
string tree2str(TreeNode* root) {
//1.初步转化:
string s1;
Preorder(root,s1);
//2.去括号:
string::iterator left = s1.end()-1;
s1.erase(left,s1.end());
return s1;
}
void Preorder(TreeNode* root,string& s)
{
if(root == nullptr)
return;
string tmp = to_string(root->val);
if(s.size()!=0)
s+="(";
s+=tmp;
Preorder(root->left,s);
if(root->left ==nullptr && root->right!=nullptr)
s+="()";
Preorder(root->right,s);
s+=")";
}
};
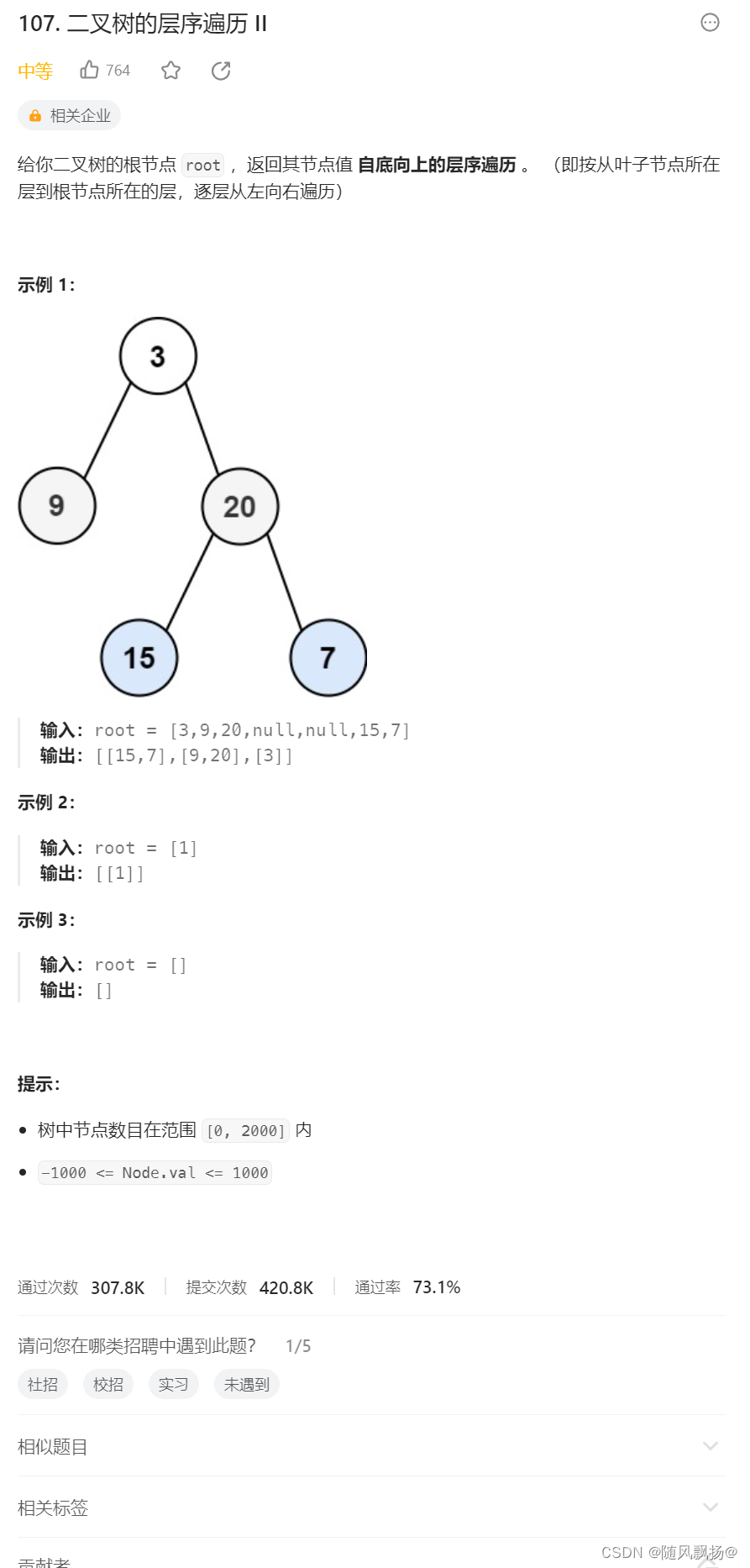
2.二叉树的层序遍历(二)
二叉树的层序遍历(二)
思路一
1.走一个正常的层序遍历利用队列这个数据结构去保存数据。
2.保存好的正常的层序遍历的数据vector<vector> vv;
3.逆置这个顺序表返回就实现了自下而上的效果。
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> vv;
if(root == nullptr)
return vv;
queue<TreeNode*> s;
s.push(root);
int num = s.size();
vector<int> tmp;
while(!s.empty())
{
TreeNode* top = s.front();
tmp.push_back(top->val);
s.pop();
num--;
if(top->left!=nullptr)
s.push(top->left);
if(top->right!=nullptr)
s.push(top->right);
if(num==0)
{
num = s.size();
vv.push_back(tmp);
tmp.resize(0);
}
}
reverse(vv.begin(),vv.end());
return vv;
}
};
3.二叉树的最近公共祖先:

二叉树的最近公共祖先
思路一:

1.判断一个节点在不在当前节点的左树中,或者右树中。
2.特殊情况的判断:当前节点为p或者q那么当前的节点就是祖先。
3时间复杂度为O(n^2);
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool Intree(TreeNode* root, TreeNode* x)
{
if(root == nullptr)
return false;
return ((root == x) ||Intree(root->left , x)||Intree(root->right , x));
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr)
return nullptr;
//1.特殊情况判断:
if(root == p || root == q)
return root;
//2.确定正常情况内容:
bool pinleft,pinright,qinleft,qinright;
pinleft = Intree(root->left , p);
pinright = !pinleft;
qinleft = Intree(root->left, q);
qinright = !qinleft;
//3.三个情况判断:
//一个左,一个右,---左左----右右
if((qinleft && pinright) || (qinright && pinleft))
return root;
else if(qinleft && pinleft)
return lowestCommonAncestor(root->left , p , q);
else if(qinright && pinright)
return lowestCommonAncestor(root->right, p , q);
assert(false);
return nullptr;
}
};
思路二:
1,优化时间复杂度为O(n)
2.思路–>空间换时间
3.获取根节点到p,q两个节点的路径。
4.相交链表找交点的思路:
class Solution {
public:
bool GetPath(TreeNode* root , TreeNode* x , stack<TreeNode*>& path)
{
if(root == nullptr)
return false;
//1.节点入栈:
path.push(root);
//2.当前节点满足情况:
if(root == x)
return true;
//3.进入左树和进入右树:
if(GetPath(root->left,x,path))
return true;
if(GetPath(root->right,x,path))
return true;
//1.当前节点的左树和右数都不满足条件!
path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr)
return nullptr;
stack<TreeNode*> _p;
stack<TreeNode*> _q;
//1.获取路径:
GetPath(root,p,_p);
GetPath(root,q,_q);
//2.进入链表找交点的过程
while(_p.size()!=_q.size())
{
if(_p.size()>_q.size())
_p.pop();
else
_q.pop();
}
while(_p.top()!=_q.top())
{
_p.pop();
_q.pop();
}
return _p.top();
}
};
GIF题目解析
4.二叉搜索树与双向链表:

二叉搜索树与双向链表:
思路一
1,二叉搜索树的中序是有序的。
2.题目要求把一个二叉搜索树转化为一个双向的链表。
3.进行中序遍历并且在过程中去调整left为前驱,right为后继指针。
4.我们不能通过后一个的左指向前一个但是可以通过前一个的右指向后一个。
5.我们通过遍历到下一个然后通过前一个的后指向当前进行调整前一个的右指针。
class Solution {
public:
void adjust(TreeNode* cur , TreeNode*& prev)
{
if(cur == nullptr)
return;
adjust(cur->left, prev);
//1.当前节点的左指向前一个:
cur->left = prev;
//2.前一个节点的右指向当前节点:
if(prev)
prev->right = cur;
//1.cur会自动更新:
prev = cur;
adjust(cur->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
TreeNode* prev = nullptr;
adjust(pRootOfTree, prev);
TreeNode* head = pRootOfTree;
while(head && head->left)
{
head=head->left;
}
return head;
}
};
![第三节课[LangChain]作业](https://img-blog.csdnimg.cn/direct/d7a15989b04f4efc806cbd0b82e94ab5.png)