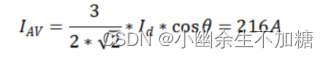难度:简单
总计有
n个环,环的颜色可以是红、绿、蓝中的一种。这些环分布穿在 10 根编号为0到9的杆上。给你一个长度为
2n的字符串rings,表示这n个环在杆上的分布。rings中每两个字符形成一个 颜色位置对 ,用于描述每个环:
- 第
i对中的 第一个 字符表示第i个环的 颜色('R'、'G'、'B')。- 第
i对中的 第二个 字符表示第i个环的 位置,也就是位于哪根杆上('0'到'9')。例如,
"R3G2B1"表示:共有n == 3个环,红色的环在编号为 3 的杆上,绿色的环在编号为 2 的杆上,蓝色的环在编号为 1 的杆上。找出所有集齐 全部三种颜色 环的杆,并返回这种杆的数量。
示例 1:
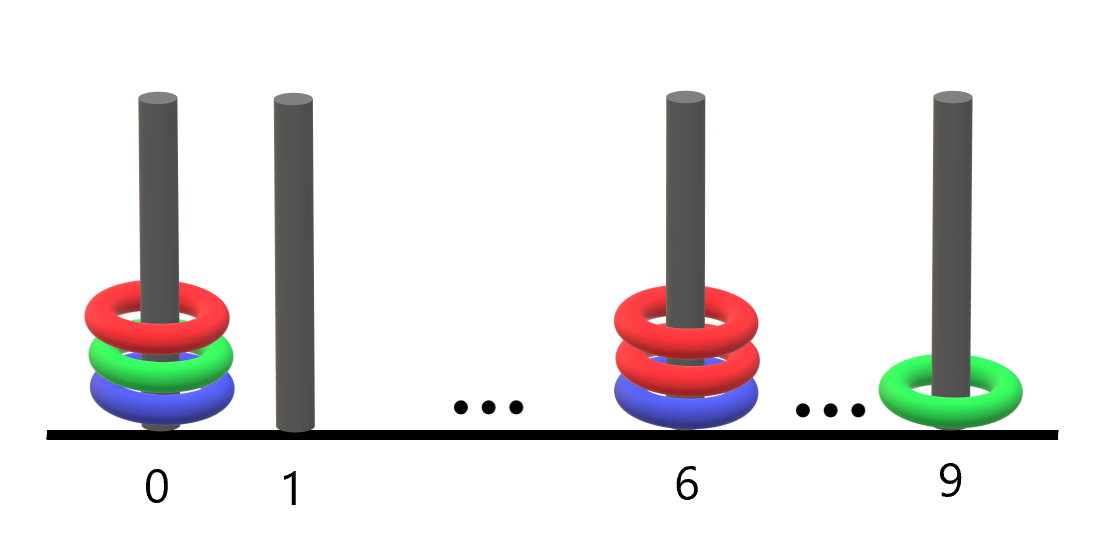
输入:rings = "B0B6G0R6R0R6G9" 输出:1 解释: - 编号 0 的杆上有 3 个环,集齐全部颜色:红、绿、蓝。 - 编号 6 的杆上有 3 个环,但只有红、蓝两种颜色。 - 编号 9 的杆上只有 1 个绿色环。 因此,集齐全部三种颜色环的杆的数目为 1 。示例 2:
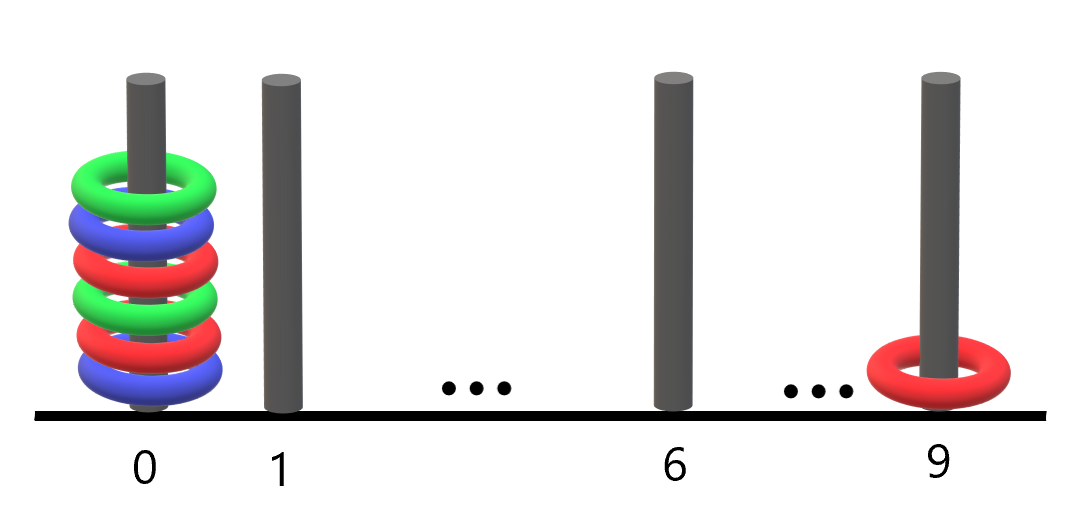
输入:rings = "B0R0G0R9R0B0G0" 输出:1 解释: - 编号 0 的杆上有 6 个环,集齐全部颜色:红、绿、蓝。 - 编号 9 的杆上只有 1 个红色环。 因此,集齐全部三种颜色环的杆的数目为 1 。示例 3:
输入:rings = "G4" 输出:0 解释: 只给了一个环,因此,不存在集齐全部三种颜色环的杆。提示:
rings.length == 2 * n1 <= n <= 100- 如
i是 偶数 ,则rings[i]的值可以取'R'、'G'或'B'(下标从 0 开始计数)- 如
i是 奇数 ,则rings[i]的值可以取'0'到'9'中的一个数字(下标从 0 开始计数)题解:
class Solution: def countPoints(self, rings: str) -> int: final_res = 0 count_zifu = {} for i in rings: if i.isdigit(): count_zifu[i] = rings.count(i) print(count_zifu) for k,v in count_zifu.items(): if v >=3 and '{}{}'.format('G',k) in rings and '{}{}'.format('R',k) in rings and '{}{}'.format('B',k) in rings: print('{}{}'.format('G',k)) final_res += 1 return final_res
leetcode:2103. 环和杆(python3解法)
news2026/2/13 21:06:09
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/144668.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
makefile 入门
make常用选项
# make 默认在当前目录中寻找GUNmakefile,makefile,Makefile的文件作为make的输入文件
# -f 可以指定默认的输入文件名,如: -f MyMakefile
# -v 显示make版本号
# -n 只输出命令,但不执行,一般用于测试
# -s 只执行命令,但不显示具体命令,与在命令中使用作用一样…
第四十四讲:神州防火墙双机热备配置
两台防火墙硬件型号和软件版本都完全相同,为了避免防火墙不堪重负而宕机引起网络中断,可以考虑应用双机热备(HA)解决方案。双机热备能够把两台防火墙构成一个工作组,一主一备,保证数据通信畅通,…
【实际开发01】- 单元测试 ( 追求正确性 )
目录
0. 单元测试 概念 / 解析
1. 为什么要进行单元测试
1. JUnit ~ Test
2. IDEA 中使用 junit 单元测试 , 不能使用 Scanner 的解决方法
3. Junit 测试 Tutorial
1. daiding
4. Test 修饰的方法必须 public
1. validatePublicVoidNoArgMethods(Test.class, false, er…
功率二极管的损耗分析和选型原则
功率二极管的损耗分析和选型原则
tip:参考网上资料,学习为主
1.二极管的分类 2.二极管的损耗组成 3.二级管的损耗分析 4.应用实例1.Flyback电源电路二极管损耗计算 5.实例应用2.BOOST电路二极管损耗计算 6.实例应用3.大功率整流桥二极管参数计算 7.选型…
sqli-labs 5~6 多命通关攻略
sqli-labs 5~6 多命通关攻略描述判断注入类型正常输入不正常输入错误输入判断 SQL 查询结果的列数猜测 SQL 查询结果中的列数为两列猜测 SQL 查询结果中的列数为三列猜测 SQL 查询结果中的列数为四列爆破方式的可行性函数 UpdateXML()爆破(报错注入)爆破…
农业智能化进入“刚需时代 ” ,维视智造机器视觉实验室赋能新农科人才培养
1、传统农业数字化转型 新农科人才急需紧缺数千年来,农业是我国立国基础,农业兴衰关系到国家的命运。在大力推动乡村振兴的背景下,高校作为强农兴农的“国之重器”,在培育“农”的传人、新农科建设方面扮演着不可替代的角色。世界…
C++入门——内联函数、extern “C“
一. 内联函数
1.概念及分析
以inline修饰的函数叫做内联函数,编译时C编译器会在调用内联函数的地方展开,没有函数调 用建立栈帧的开销,内联函数提升程序运行的效率。
int Add(int a, int b)
{int c a b;return c;
}int main()
{int re…
聚焦技术创新实力,时序数据库 TDengine 荣登中国技术先锋年度评选两大榜单
2023 年 1 月 5 日,中国技术先锋年度评选 | 2022 中国最受开发者欢迎的技术活动榜单正式发布。作为中国领先的新一代开发者社区,SegmentFault 思否依托社区活动板块及全站数百万开发者用户行为数据,及活动规模、内容好评度、行业综合影响力指…
Go语言设计与实现 --调度器(详细介绍)
GMP和GM模型
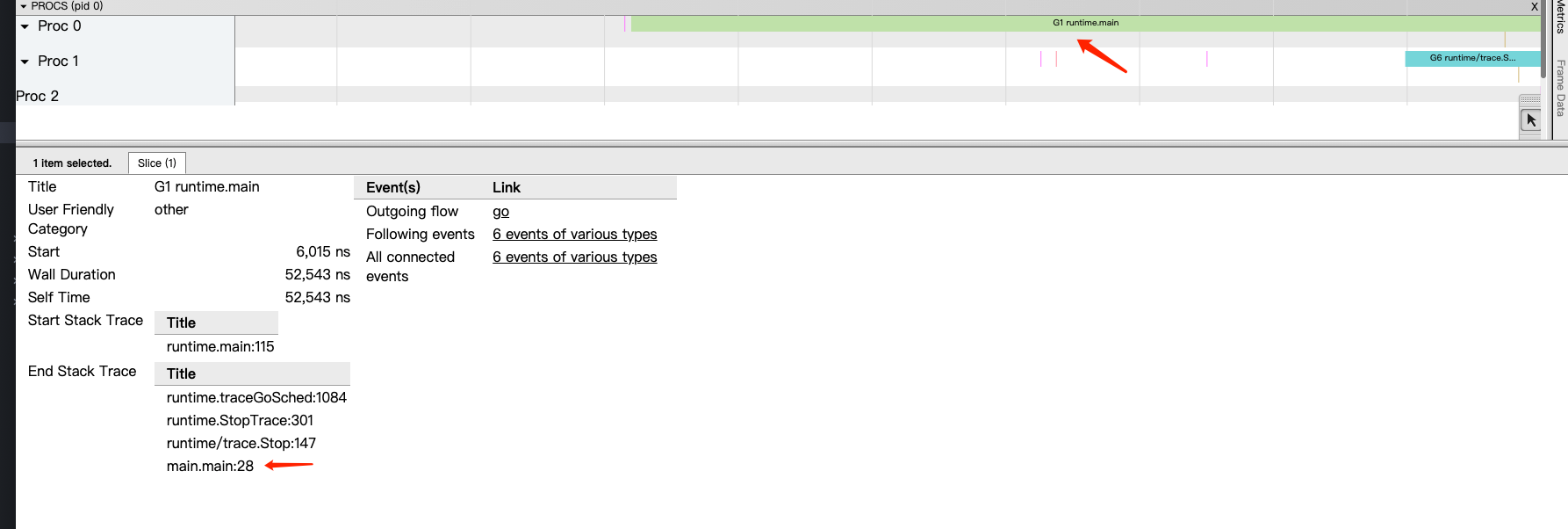
先来一张图: G(Goroutine):代表Go 协程Goroutine,存储了 Goroutine 的执行栈信息、Goroutine 状态以及 Goroutine 的任务函数等。G的数量无限制,理论上只受内存的影响,创建一个 G 的初始栈大小为2-4K&…
vue项目安装使用element_UI
安装element_UI之前需要安装VUE脚手架框架! 第一步: 在Vscode 随意打开一个文件夹,在集成终端打开 npm i -g vue/cli (检测: vue -V) 第二步:新建一个文件夹,并且在集成终端打开安装VUE脚手架 需要输入命令: vue create yan6 //yan6 为自定义文件名 1: 选第三个自定义 2: 将…
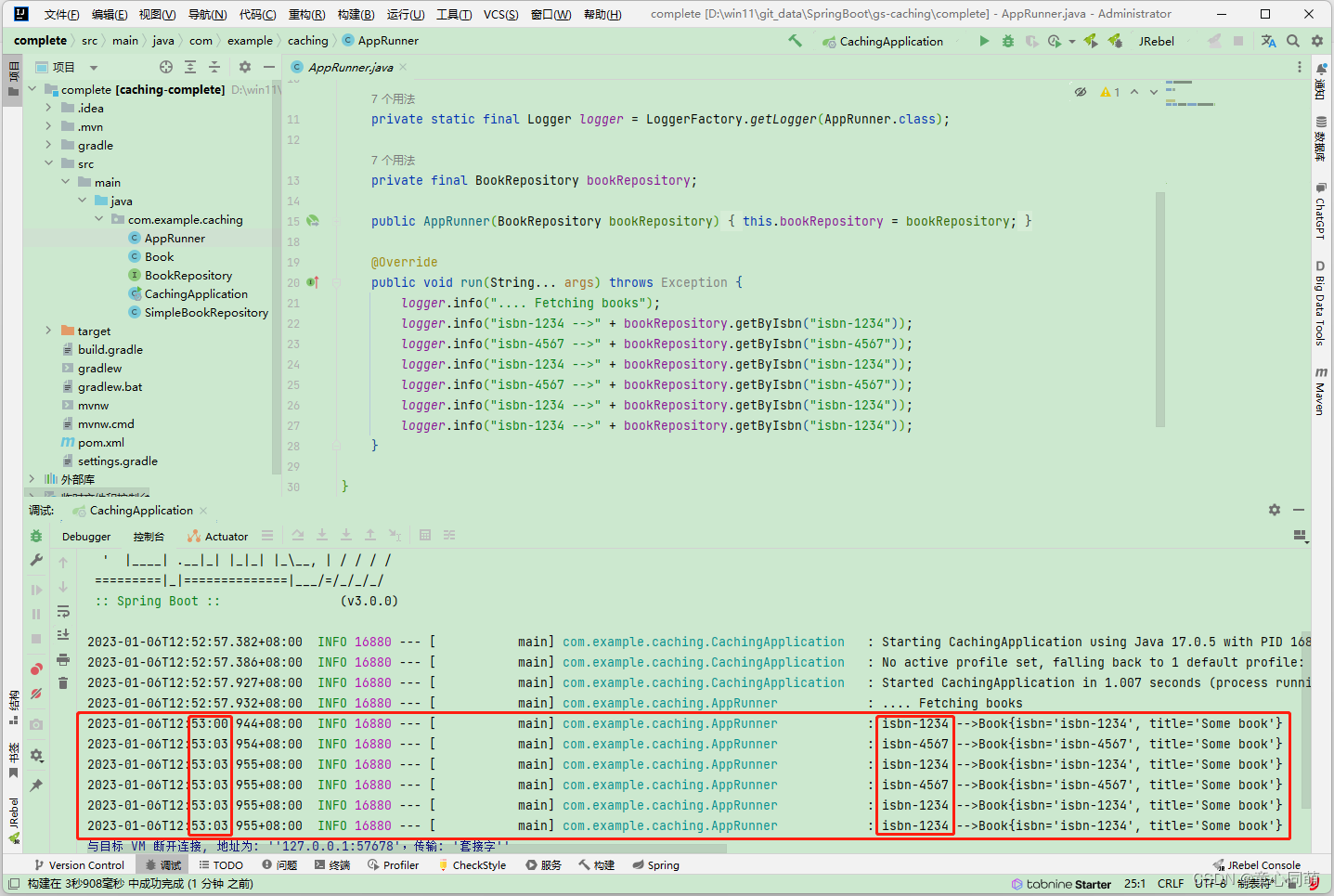
SpringBoot缓存数据(官方案例)
在线文档项目结构 1.源码克隆:git clone https://github.com/spring-guides/gs-caching.git
2.包含两个项目initial和complete,initial可以根据文档练习完善,complete是完整项目
3.功能描述:构建应用程序,在图书存储库…
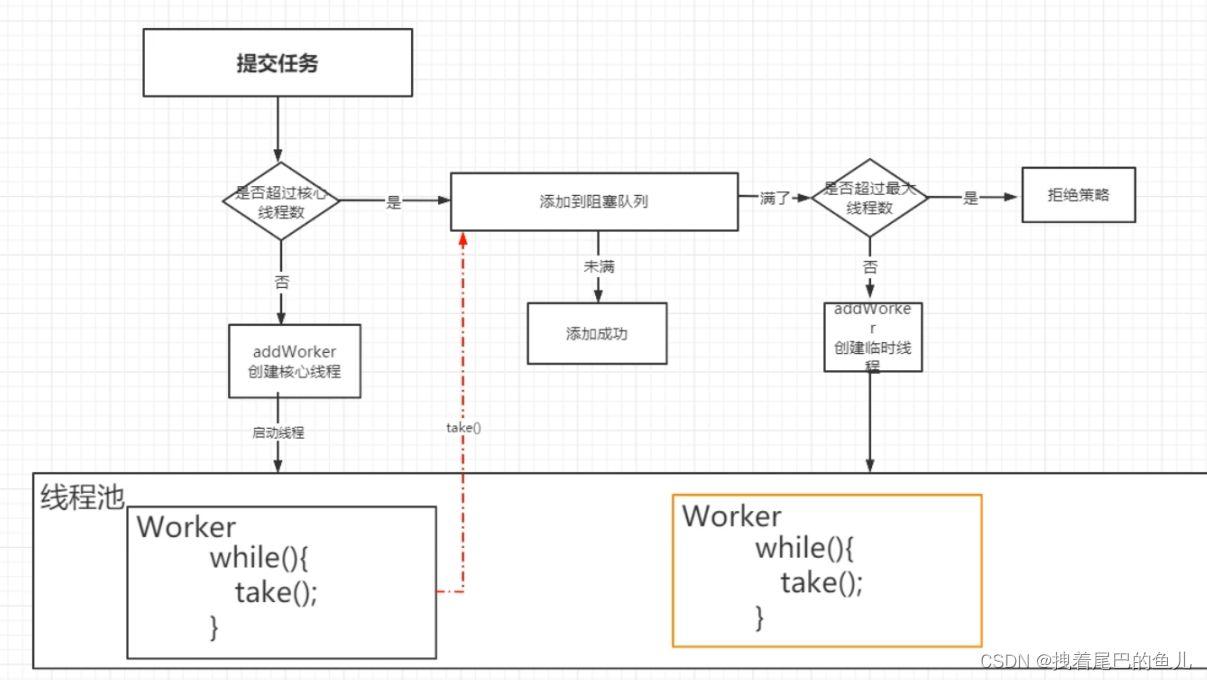
JAVA并发编程工具篇--1理解线程池任务的执行和线程的销毁
前言:在编程中我们为什么要使用线程池,线程池中的线程是怎么执行任务的,线程池中的线程是如何复用和销毁的;
1 什么是线程池: 提前创建一些线程放到一个地方,使用的时候直接获取,避免频繁的创建…
CalDAV网页客户端AgenDAV
什么是 AgenDAV ? AgenDAV 是一个类似于 Google 日历的 CalDAV 网络客户端,具有 AJAX 界面,允许用户管理自己的日历和共享的日历。 注意事项
AgenDAV依赖于 CalDAV 服务器(Bakal、DAViCal 等),所以需要先安…
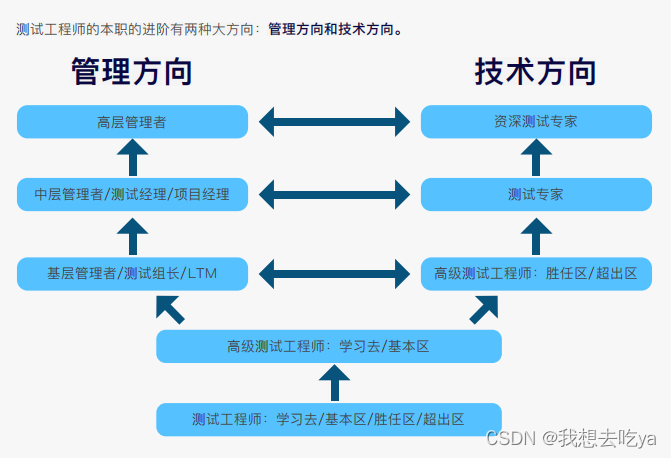
软件测试员在面试中常遇问题
目前,疫情已经逐渐得到了控制,各行各业都掀起了复工大潮。与此同时,软件测试的招聘需求也随着复工的开始而变得紧急起来,而求职者应该怎样抓住机会进行应聘呢?首先最重要的就是多刷面试题,这样才能才面试过…
CSS权威指南(五)字体
文章目录1.字体族2.font-face3.字重(font-weight)4.字号(font-size)5.字形(font-style)6.字体拉伸(font-stretch)7.字距(font-kerning)8.字体变形(…
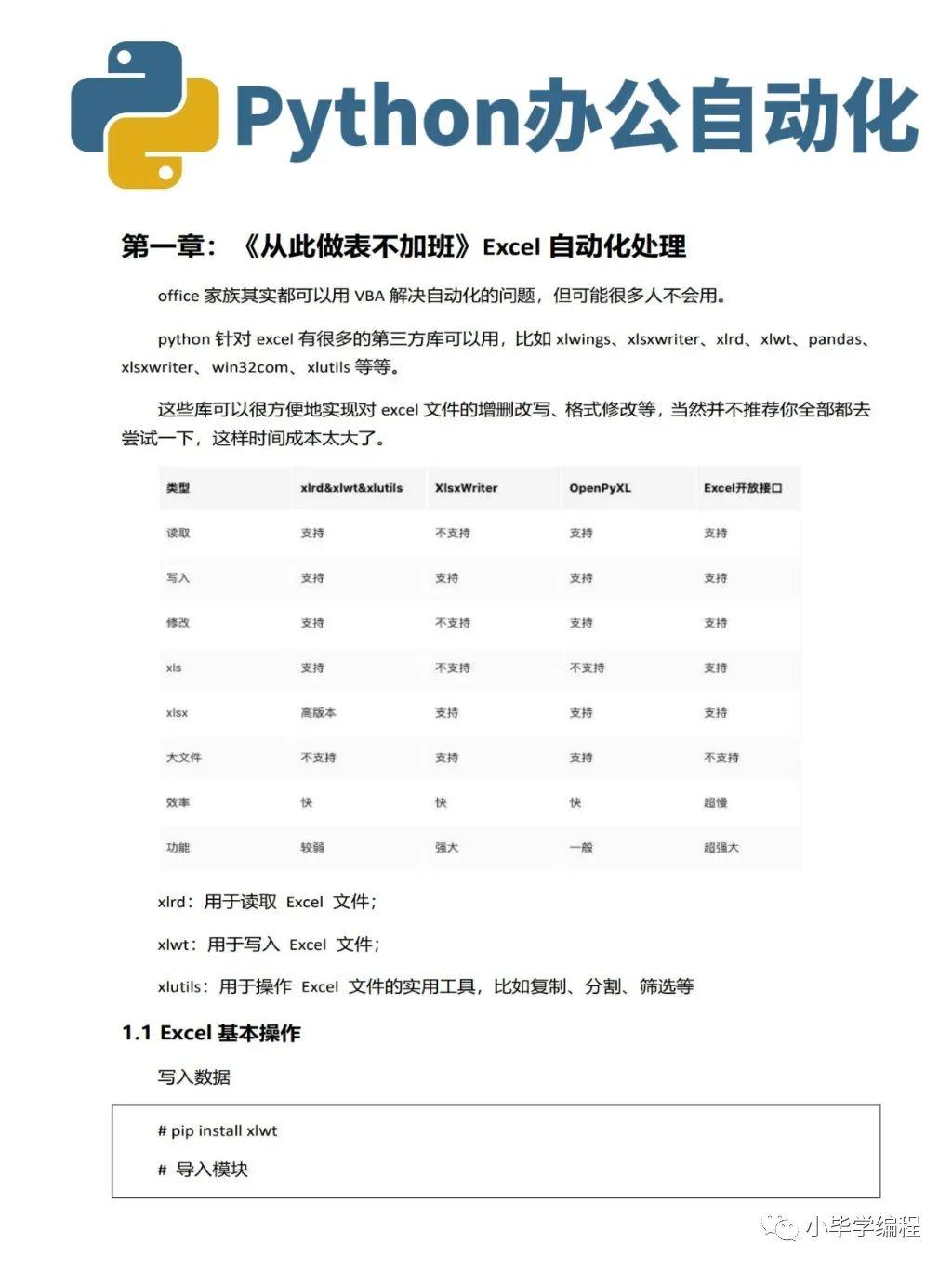
Python 办公自动化,全网最全整理来了!拒绝无效率加班!
大家好,今天给大家分享一篇 Python 自动化办公干货,整整42个实战项目案例。每一个项目案例都有详细的视频讲解,是一套非常全面的Python自动化办公项目,建议大家收藏后学习,梳理不易,记得点赞支持。详细目录…
【菜菜的CV进阶之路 - 深度学习环境搭建】常用软件安装
四、安装网易云
双系统装完了,下一步当然是,休息一下,听一首歌啦~
1、连网:只能使用wifi连,网线直连的话,还需要配置
2、安装网易云: 下载最新的Linux安装包,然后
sudo apt inst…
数据的存储(C语言)
数据类型: 要了解数据是如何存储的,我们就得先知道C语言中的数据类型 基本数据类型 基本数据类型,也就是C语言内置类型: char -> 字符型 short -> 短整型 int -> 整…
html textarea 插入字符在光标处
textarea 插入字符在光标处前言深度解析1 效果图上代码前言
深度解析
1 效果图 上代码
<!DOCUMENT><html><head>
<link rel"stylesheet" href"https://cdnjs.cloudflare.com/ajax/libs/font-awesome/4.7.0/css/font-awesome.min.css&qu…
Semantic Segmentation | 评价指标代码解析
如有错误,恳请指出。 文章目录1. 定义解析2. 代码解析之前有记录过关于图像语义分割的相关评价指标与经典网络,在看PointNet的语义分割训练脚本的时候,图像的语义分割和点云的语义分割其实本质上是一致的。所以这里想记录一下语义分割的评价指…