目录
创建二叉树
整体思路
代码实现
图示理解
销毁二叉树
判断二叉树是否是完全二叉树&层序
整体思路
代码实现
图是理解
二叉树的性质
题目
创建二叉树
整体思路
- 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
- 遇到#就回退,返回NULL,链接到上层递推的左边/右边
- 开辟节点,按照前序(根左右)的顺序。放入元素到开辟的空间。
- 递退下去的是左节点就链接到左边
- 递退下去的是右节点就链接到右边
- return root 返回节点链接到上层的左边/右边
代码实现
//创建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode*));
root->data = a[(*pi)++];
root->left = BinaryTreeCreat(a, pi);
root->right = BinaryTreeCreate(a, pi);
return root;
}图示理解
销毁二叉树
- 销毁二叉树前序/中序/后序都可以
- 后序最方便,不需要先保存左右孩子
- 形式参数是实际参数的一份临时拷贝。(置空有两种方法)
- 方法1:指针的指针
- 方法2:在main函数里面销毁
- ❗一定要销毁
- 函数return之前
- 使用了动态内存开辟的地方都要销毁
//销毁二叉树
void BinaryTreeDestory(BTNode** root)
{
if (*root == NULL)
return;
BinaryTreeDestory(*((*root)->left));//❌
BinaryTreeDestory(*((*root)->right));
free(*root);
*root = NULL;
}//销毁二叉树
#include<stdio.h>
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
}
int main()
{
BTNode* root = CreatBinaryTree();
BinaryTreeDestory(root);
root=NULL;
return 0;
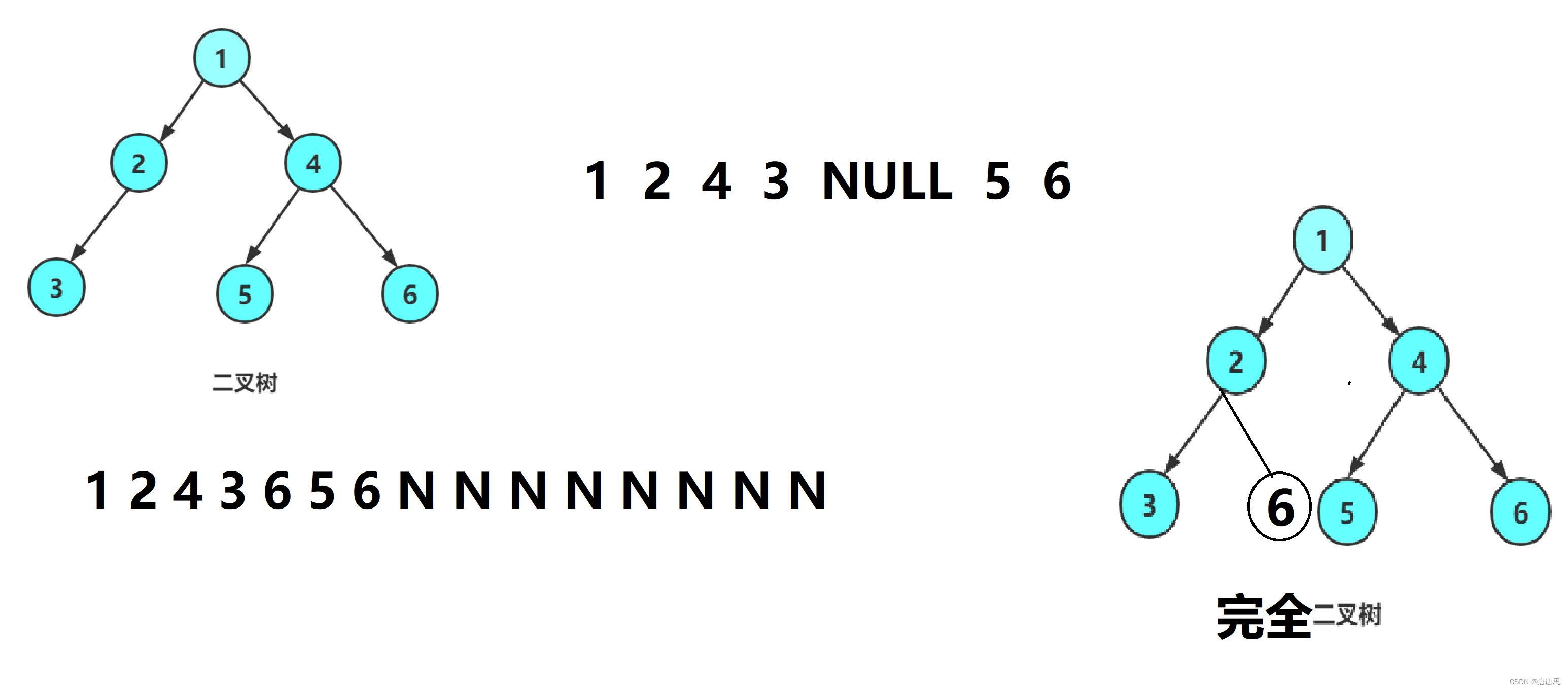
}判断二叉树是否是完全二叉树&层序
整体思路
- 完全二叉树一层一层(层序遍历)走,就是连续的
- 只要不连续就不是完全二叉树
- 层序遍历(全部元素都入队列❗空也入队列)
- 遇到空了就跳出循环
- 进入另外一个循环
- 查看从空开始后面的元素是否都是NULL
- 若全是NULL则证明是完全二叉树
- 若还有元素则证明不是完全二叉树
- 注意❗return之前记得要销毁
代码实现
//判断完全二叉树
int BinaryTreeComplete(BTNode* root)
{
Queue pq;
QueueInit(&pq);
if (root)
QueuePush(&pq, root);
while (!QueueEmpty(&pq))
{
BTNode* tmp = QueueFront(&pq);//队列头的元素
QueuePop(&pq);//出元素到队头
if (tmp == NULL)
{
break;
}
QueuePush(&pq, tmp->left);
QueuePush(&pq, tmp->right);
}
while (!QueueEmpty(&pq))//队列里面的元素个数)
{
if (QueueFront(&pq))
{
QueueDestroy(&pq);
return false;
}
QueuePop(&pq);//出元素到队头
}
QueueDestroy(&pq);
return true;
}图是理解
二叉树的性质
- 对任何一棵二叉树,如果度为0其叶结点个数为n0, 度为2的分支结点个数为n2 ,则有n0=n2+1
- 其他结论前面都已论证过了
- 一棵树节点个数=度为0(叶子节点)+度为1+度为2



题目
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为
A 不存在这样的二叉树
B 200
C 198
D 199
2.下列数据结构中,不适合采用顺序存储结构的是
A 非完全二叉树
B 堆
C 队列
D 栈
3.在具有 2n 个结点的完全二叉树中,叶子结点个数为
A n
B n+1
C n-1
D n/2
4.一棵完全二叉树的节点数位为531个,那么这棵树的高度为
A 11
B 10
C 8
D 12
5.一个具有767个节点的完全二叉树,其叶子节点个数为
A 383
B 384
C 385
D 386
答案:BAABB
【第三题】

大家可以自己尝试写第五题??
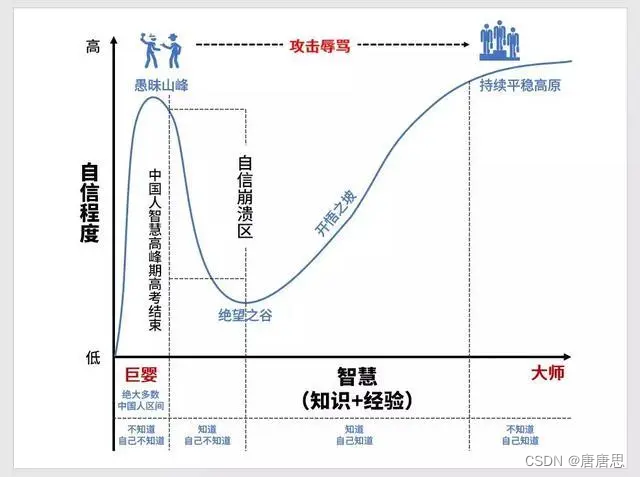
达克效应。最近这个多度递归,大概已经到了我的自信奔溃区了。
🙂感谢大家的阅读,若有错误和不足,本章初阶学习二叉树就结束了,下篇进入排序。欢迎指正。大家新年快乐!!


![Gazebo无法显示模型 [Err] [InsertModelWidget.cc:403] Missing model.config for model](https://img-blog.csdnimg.cn/direct/6c7908f8dfff4c1bb678092e2d962f35.png#pic_center)






![[1-docker-01]centos环境安装docker](https://img-blog.csdnimg.cn/direct/6dba3d59df004523973f1e7c35c5f7d5.png)