多旋翼无人机升空飞行的首要条件是动力，有了动力才能驱动旋粪旋转，才能产生克服重力所必需的升力。使旋翼产生升力，进而推动多旋翼无人机升空飞行的一套设备装置称为动力装置，包括多旋翼无人机的发动机以及保证发动机正常工作所必需的附属系统和附件。

多旋翼飞行器是通过调节多个电机转速来改变螺旋桨转速，实现升力的变化，进而达到飞行姿态控制的目的。

多旋翼飞行原理详解

以四旋翼飞行器为例，飞行原理如下图所示，电机1和电机3逆时针旋转的同时，电机2和电机4顺时针旋转，因此飞行器平衡飞行时，陀螺效应和空气动力扭矩效应全被抵消。与传统的直升机相比，四旋翼飞行器的优势：各个旋翼对机身所产生的反扭矩与旋翼的旋转方向相反，因此当电机1和电机3逆时针旋转时，电机2和电机4顺时针旋转，可以平衡旋翼对机身的反扭矩。

一般情况下，多旋翼飞行器可以通过调节不同电机的转速来实现4个方向上的运动，分别为：垂直、俯仰、横滚和偏航。

垂直运动，即升降控制

在图（a）中，两对电机转向相反，可以平衡其对机身的反扭矩，当同时增加四个电机的输出功率，旋翼转速增加使得总的拉力增大，当总拉力足以克服整机的重量时，四旋翼飞行器便离地垂直上升；反之，同时减小四个电机的输出功率，四旋翼飞行器则垂直下降，直至平衡落地，实现了沿z轴的垂直运动。当外界扰动量为零时，在旋翼产生的升力等于飞行器的自重时，飞行器便保持悬停状态。保证四个旋翼转速同步增加或减小是垂直运动的关键。

俯仰运动，即前后控制

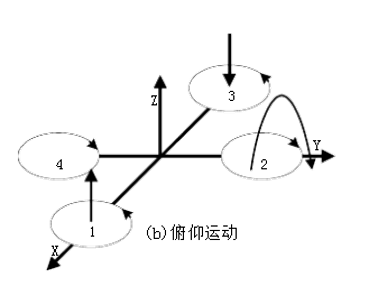
在图（b）中，电机1的转速上升，电机3的转速下降，电机2、电机4的转速保持不变。为了不因为旋翼转速的改变引起四旋翼飞行器整体扭矩及总拉力改变，旋翼1与旋翼3转速该变量的大小应相等。由于旋翼1的升力上升，旋翼3的升力下降，产生的不平衡力矩使机身绕y轴旋转（方向如图所示），同理，当电机1的转速下降，电机3的转速上升，机身便绕y轴向另一个方向旋转，实现飞行器的俯仰运动。

横滚运动，即左右控制

与图（b）的原理相同，在图（c）中，改变电机2和电机4的转速，保持电机1和电机3的转速不变，便可以使机身绕x轴方向旋转，从而实现飞行器横滚运动。

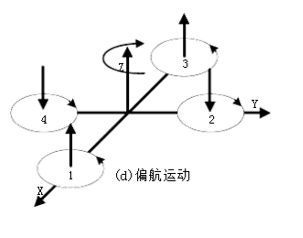
偏航运动，即旋转控制

四旋翼飞行器偏航运动可以借助旋翼产生的反扭矩来实现。旋翼转动过程中由于空气阻力作用会形成与转动方向相反的反扭矩，为了克服反扭矩影响，可使四个旋翼中的两个正转，两个反转，且对角线上的各个旋翼转动方向相同。反扭矩的大小与旋翼转速有关，当四个电机转速相同时，四个旋翼产生的反扭矩相互平衡，四旋翼飞行器不发生转动；当四个电机转速不完全相同时，不平衡的反扭矩会引起四旋翼飞行器转动。在图（d）中，当电机1和电机3的转速上升，电机2和电机4的转速下降时，旋翼1和旋翼3对机身的反扭矩大于旋翼2和旋翼4对机身的反扭矩，机身便在富余反扭矩的作用下绕z轴转动，从而实现飞行器的偏航运动。

多旋翼无人机的飞行原理主要是基于动力学原理和电机控制技术。其核心是利用多个电机和旋翼的旋转产生升力，进而实现无人机的垂直起降、悬停、前进、后退、左右移动以及偏航等运动。

具体来说，多旋翼无人机通过电子调速器（电调）控制电机转动，电机带动旋翼旋转产生升力。当升力大于无人机的重力时，无人机就能垂直起飞；当升力等于无人机的重力时，无人机就能悬停；当升力小于无人机的重力时，无人机就会垂直降落。

多旋翼无人机的飞行原理主要依赖于电机控制技术以及各个旋翼的协调旋转产生的合力。不同型号和规格的多旋翼无人机可能会有不同的飞行原理和操作方式，但基本原理是一致的。