一、说明
自从 AlexNet 在 2012 年赢得 ImageNet 竞赛以来,卷积神经网络 (CNN) 就变得无处不在。从不起眼的 LeNet 到 ResNets 再到 DenseNets,CNN 无处不在。
您是否想知道 CNN 的反向传播中会发生什么,特别是反向传播在 CNN 中的工作原理。如果您读过反向传播,您就会了解它是如何在具有全连接层的简单神经网络中实现的。 (Andrew Ng 在 Coursera 上的课程对此做了很好的解释)。但是,对于我的一生,我无法理解反向传播如何与卷积层一起工作。
我知道,您不必了解反向传播的数学复杂性即可实现 CNN。您不必手动实现它们。因此,大多数深度学习书籍也没有涵盖它。

这篇文章最重要的是向您展示这一点:
我们都知道卷积层的前向传递使用卷积。但是,反向传播期间的反向传递也使用了卷积!
但如果您已经了解反向传播中的链式法则,那么您可以跳到下一节。
二、了解反向传播中的链式法则
考虑这个方程
f(x,y,z) = (x + y)z
为了让它更简单,让我们把它分成两个方程。

现在,让我们为其绘制一个计算图,其中 x、y、z 的值为x = -2、y = 5、z = 4。
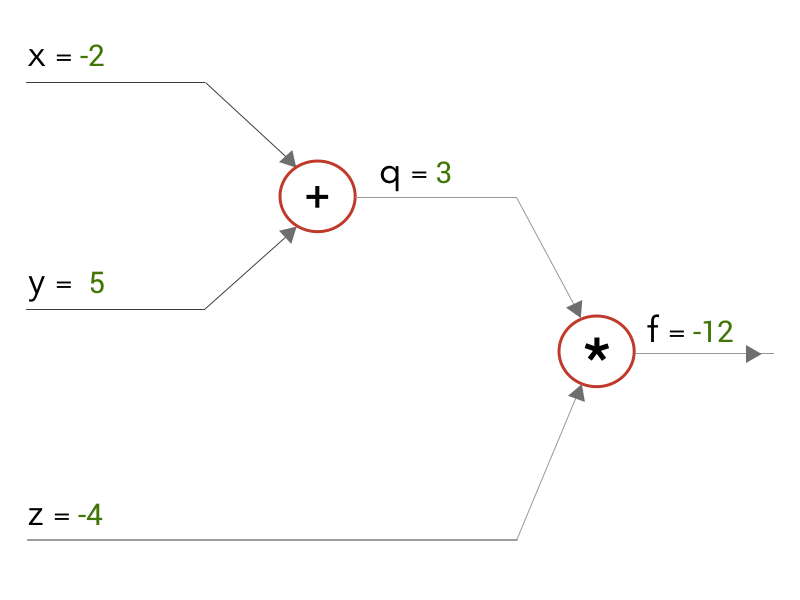
f = q*z 的计算图,其中 q = x + y
当我们求解方程时,当我们从左向右移动时(“前向传递”),我们得到的输出为f = -12
现在让我们进行向后传递。比如说,就像在反向传播中一样,我们在每个阶段导出从右到左移动的梯度。因此,最后,我们必须得到输入 x、y 和 z 的梯度值 — ∂f/∂x和 ∂f/∂y和∂f/∂z(用 x 来区分函数 f, y 和 z)
从右到左,在乘法门处,我们可以对f进行微分以获得q和z处的梯度— ∂f/∂q和∂f/∂z。在加法门,我们可以对q进行微分以获得x和y处的梯度— ∂q/∂x和∂q/∂y。
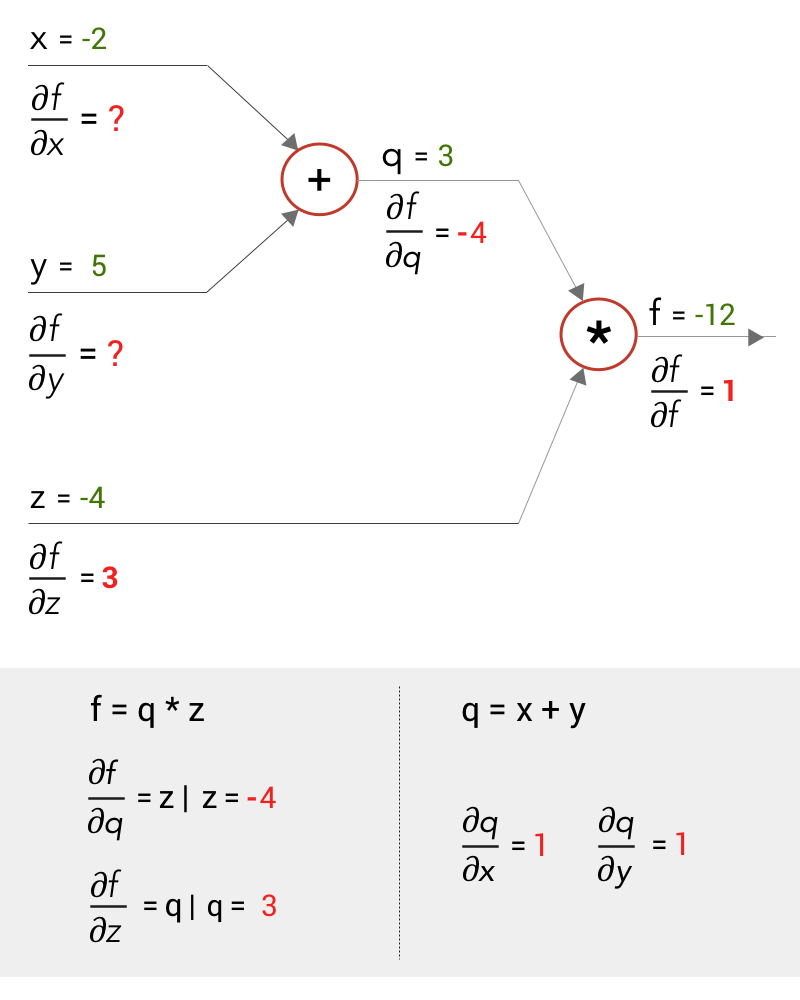
我们必须找到∂f/∂x和∂f/∂y ,但我们只得到∂q/∂x和∂q/∂y的值。那么,我们该怎么做呢?
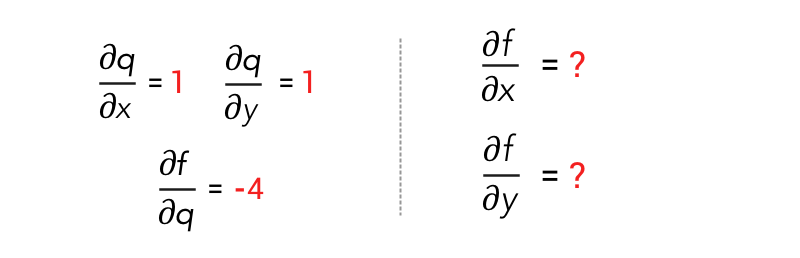
这可以使用微分链式法则来完成。根据链式法则,我们可以求出∂f/∂x为
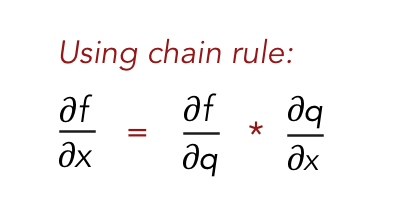
我们可以将∂f/∂x和∂f/∂y计算为:
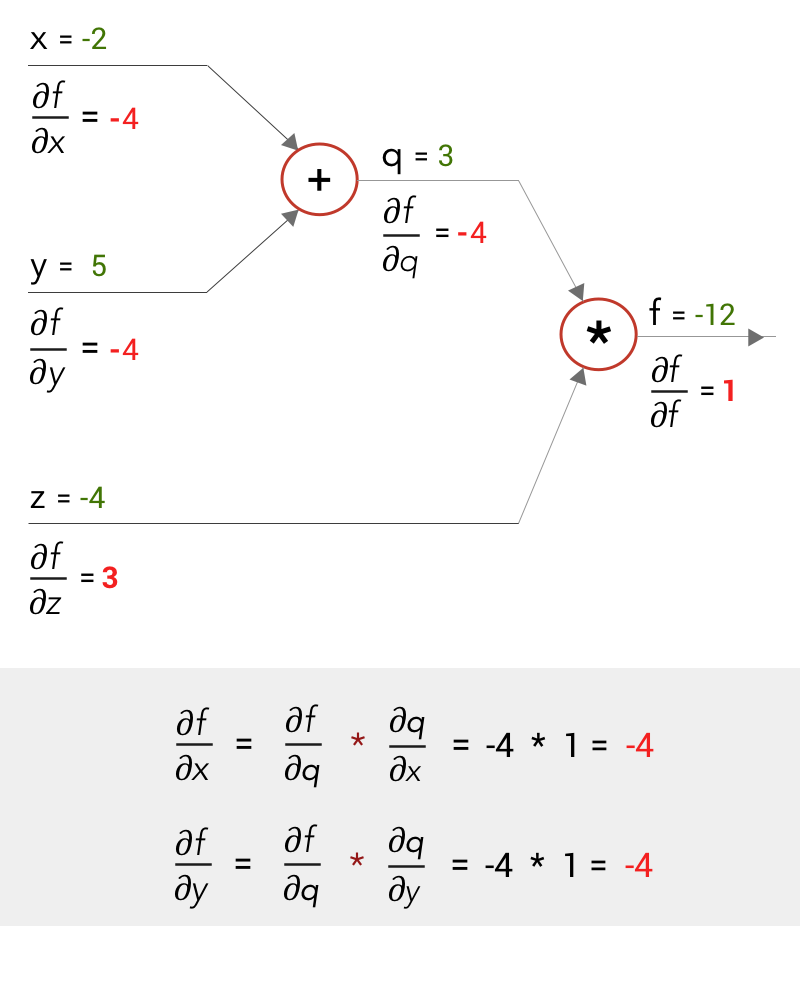
三、卷积层中的链式法则
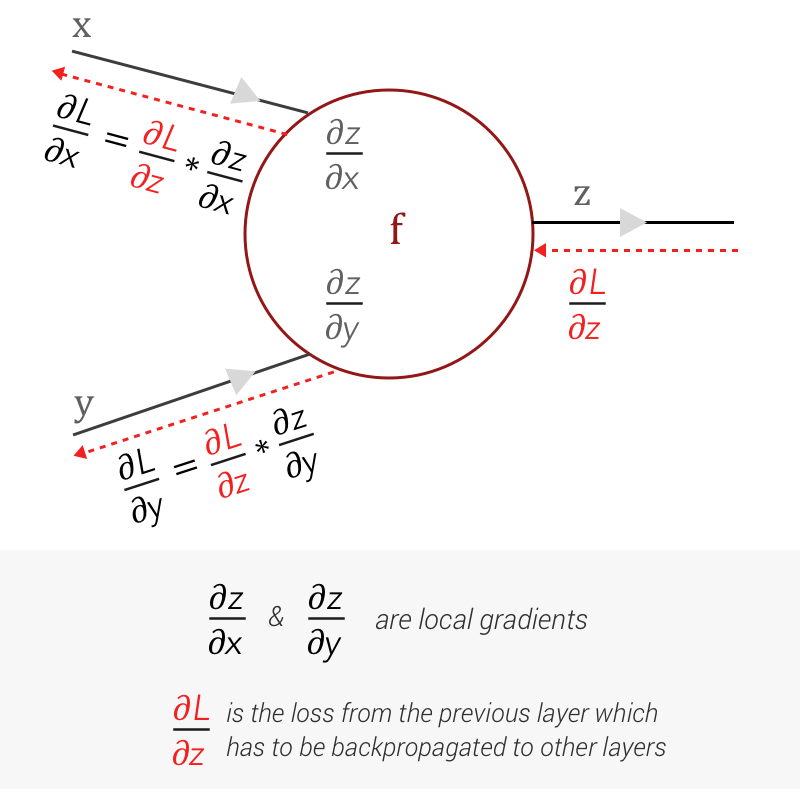
现在我们已经完成了一个简单的计算图,我们可以将 CNN 想象成一个巨大的计算图。假设计算图中有一个门f,输入为x 和 y,输出为z。
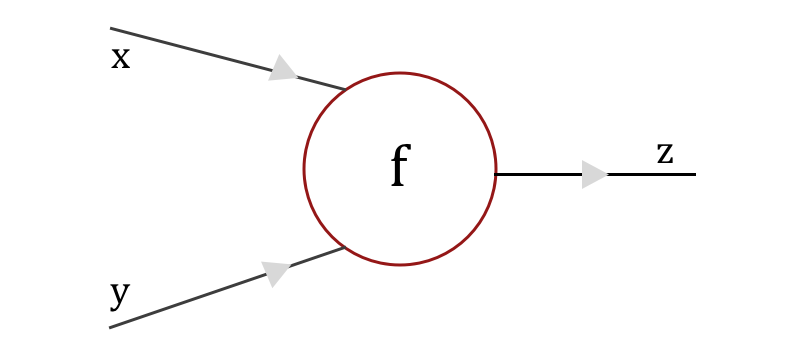
我们可以轻松计算局部梯度——将 z 相对于 x 和 y 微分为∂z/∂x和∂z/∂y
对于前向传播,我们穿过 CNN,遍历其各层,最后使用损失函数获得损失。当我们开始逐层向后计算损失时,我们从前一层得到损失的梯度为∂L/∂z。为了将损失传播到其他门,我们需要找到∂L/∂x和∂L/∂y。
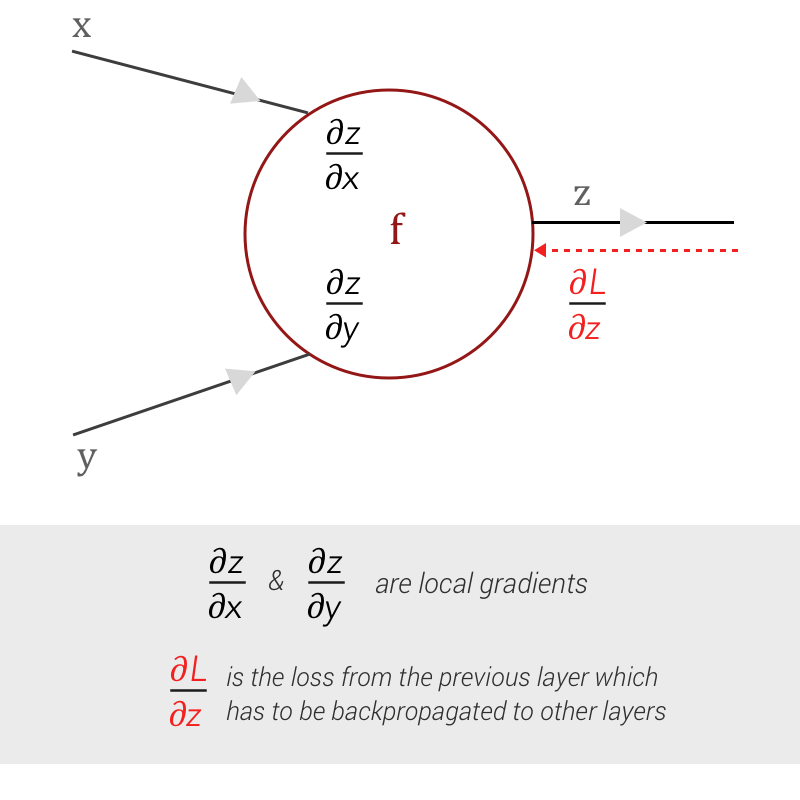
链式法则对我们有帮助。使用链式法则,我们可以计算∂L/∂x和∂L/∂y,这将馈送到扩展计算图中的其他门
那么,这与 CNN 卷积层中的反向传播有什么关系呢?
现在,假设函数f 是输入 X 和滤波器 F之间的卷积。输入 X 是 3x3 矩阵,滤波器 F 是 2x2 矩阵,如下所示:
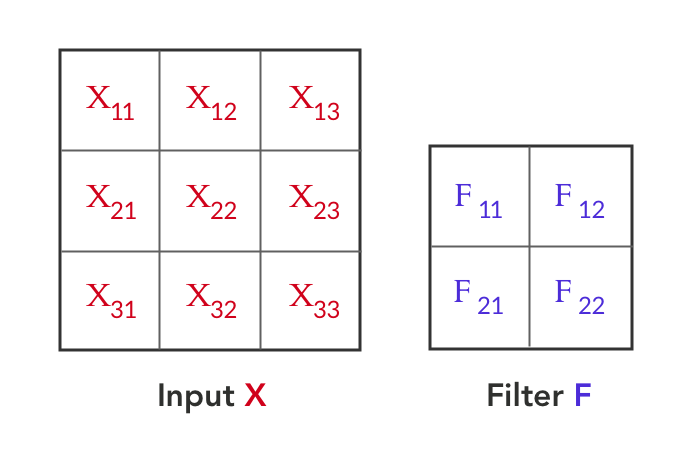
输入 X 和滤波器 F 之间的卷积得到输出 O。这可以表示为:

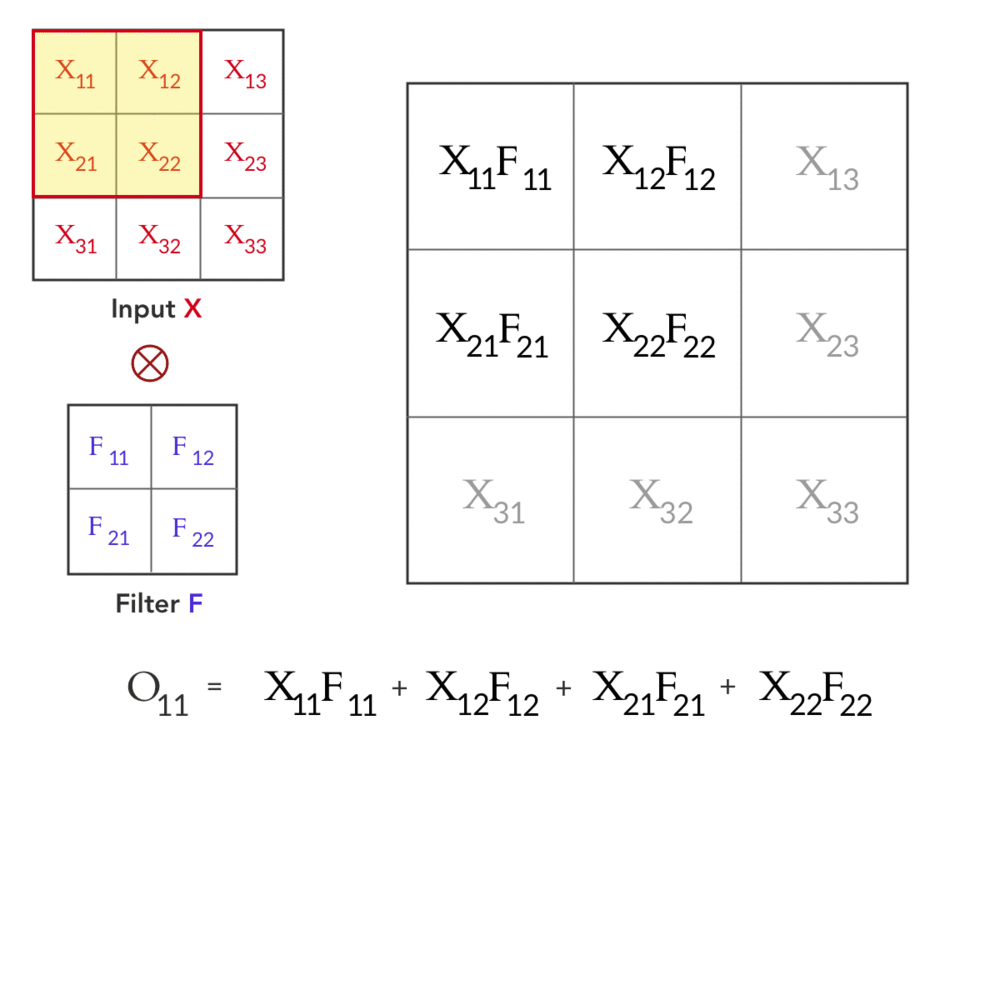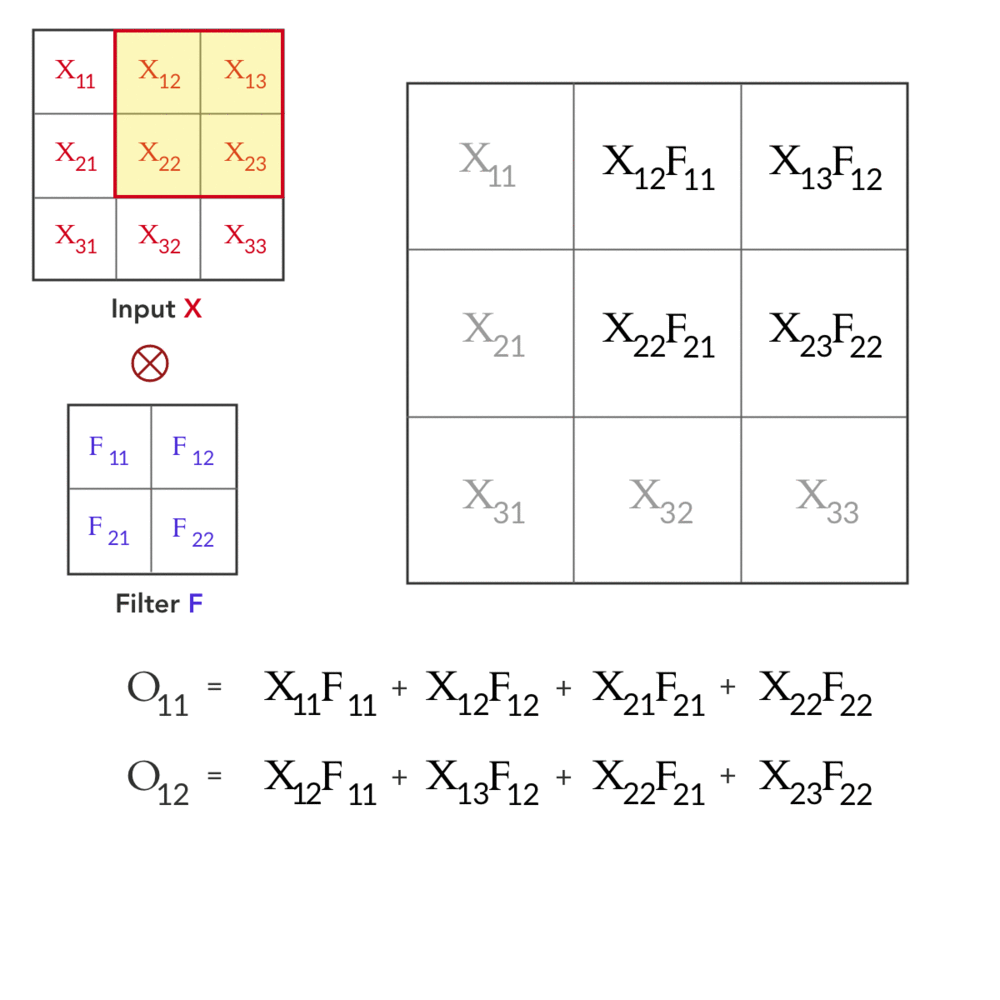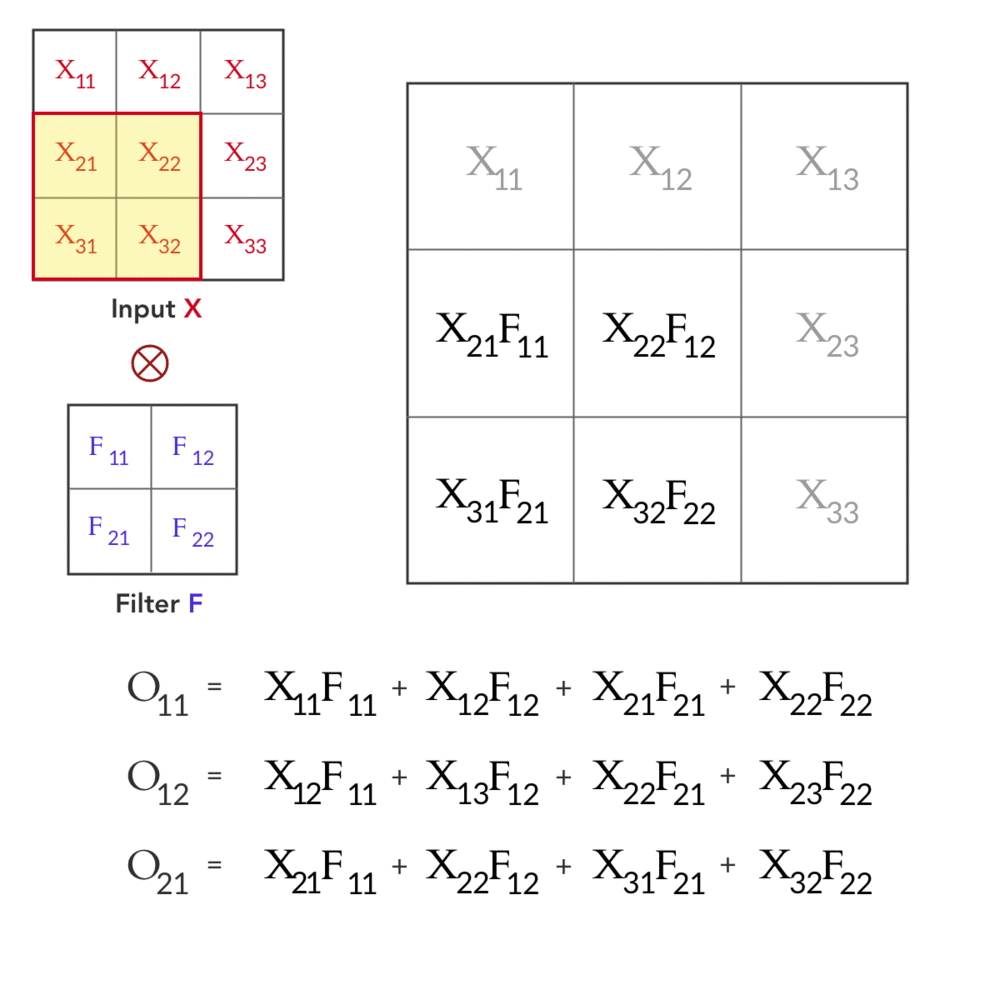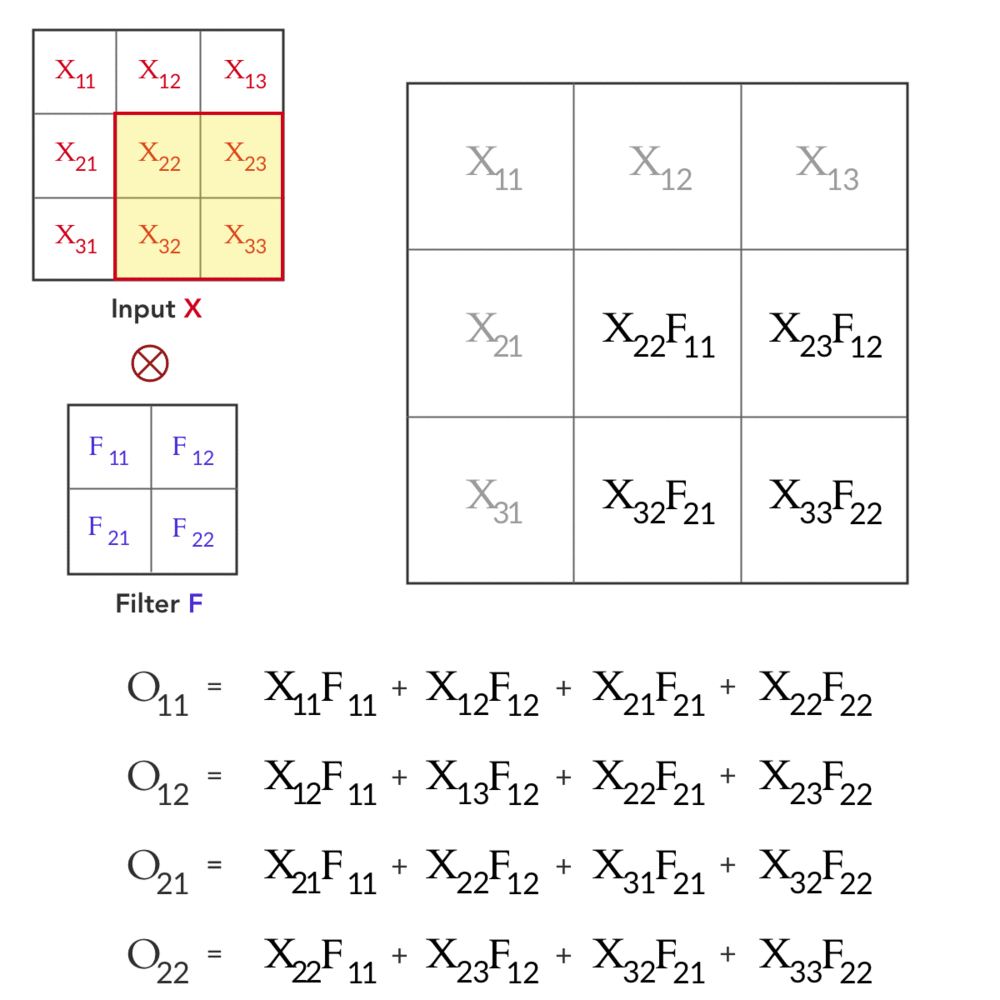
这给了我们前向传球!让我们来看看向后传递。如前所述,在向后传递期间,我们得到相对于下一层输出 O 的损失梯度为∂L/∂O。结合我们之前使用链式法则和反向传播的知识,我们得到:

如上所示,我们可以找到相对于输出 O 的局部梯度∂O/∂X和∂O/∂F 。利用前几层的损失梯度 — ∂L/∂O并使用链式法则,我们可以计算∂L /∂X和∂L/∂F。
好吧,但是为什么我们需要找到∂L/∂X和∂L/∂F呢?
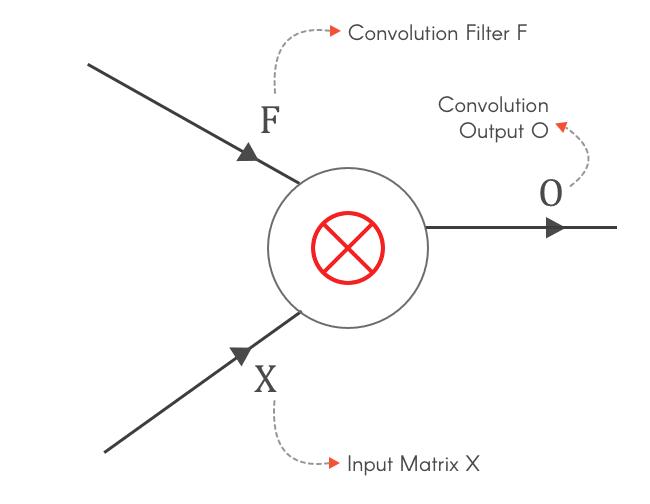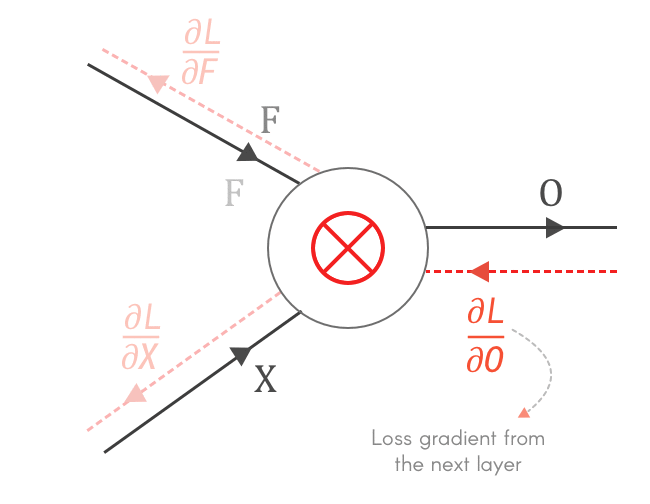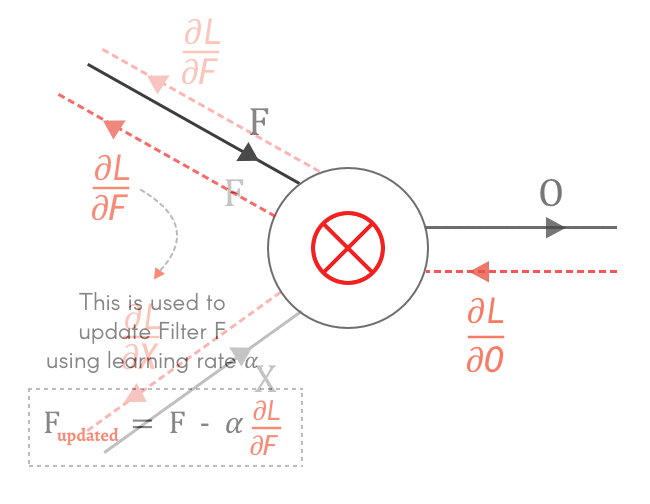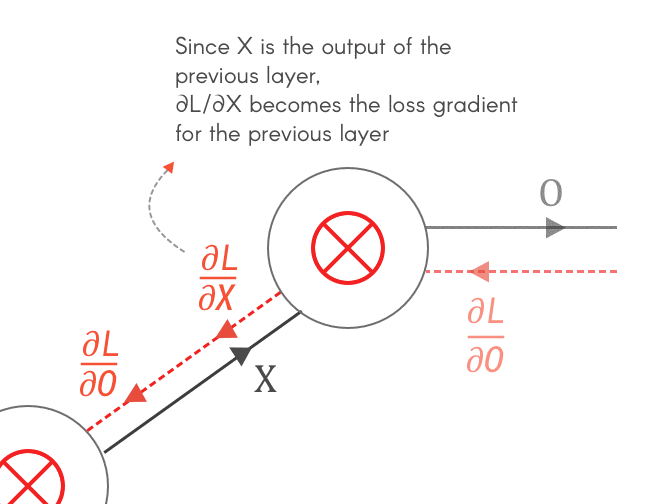
四、所以我们来求 X 和 F 的梯度 — ∂L/∂X和∂L/∂F
4.1 求 ∂L/∂F
正如我们之前所做的那样,这有两个步骤。
- 求局部梯度∂O/∂F
- 使用链式法则求∂L/∂F
步骤 1:求局部梯度 — ∂O/∂F:
这意味着我们必须区分输出矩阵 O 和滤波器 F。通过我们的卷积运算,我们知道这些值。因此,让我们开始区分 O- O11 的第一个元素与 F — F11 、 F12、F21 和 F22 的元素
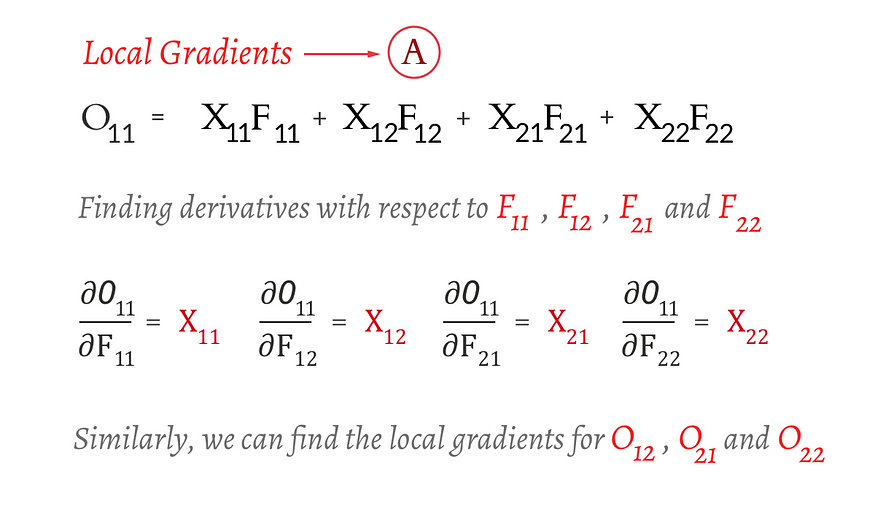
步骤 2:使用链式法则:
正如我们之前的例子中所描述的,我们需要找到∂L/∂F:
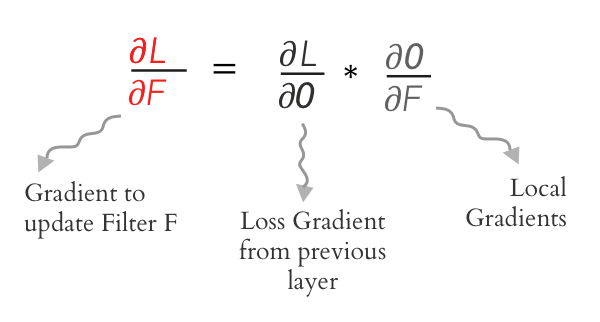
O和F是矩阵。并且∂O/∂F将是矩阵O对于矩阵F的偏导数!最重要的是我们必须使用链式法则。这看起来确实很复杂,但幸运的是我们可以使用下面的公式来扩展它。
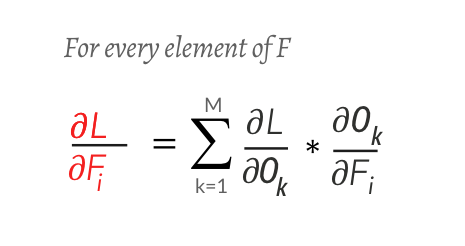
展开,我们得到..

将方程 A 中的局部梯度值 — ∂O/∂F 代入,我们得到
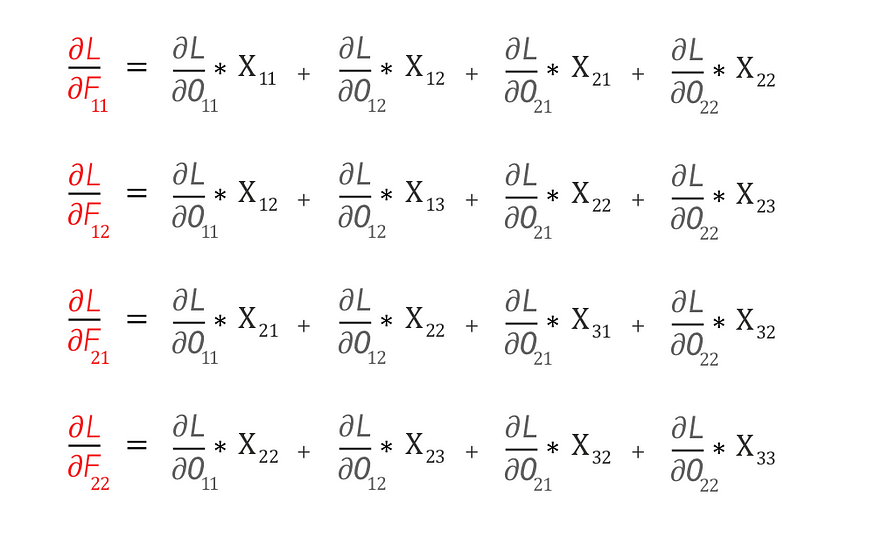
如果你仔细观察的话,这就是我们非常熟悉的操作。我们可以将其表示为输入 X和损失梯度∂L/∂O 之间的卷积运算,如下所示:
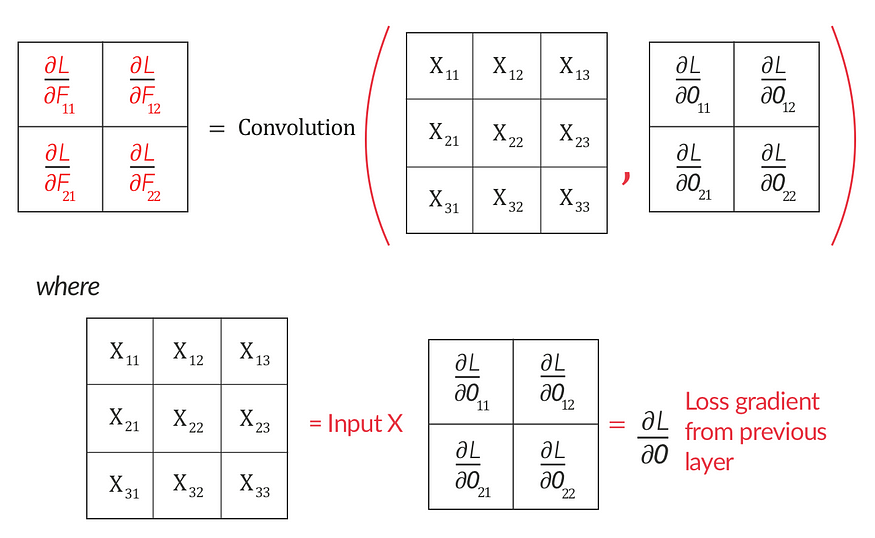
∂L/∂F 只不过是输入 X 和下一层的损失梯度 ∂L/∂O 之间的卷积
4.2 求 ∂L/∂X:
步骤 1:求局部梯度 — ∂O/∂X:
与我们之前找到局部梯度的方式类似,我们可以找到∂O/∂X:

步骤 2:使用链式法则:
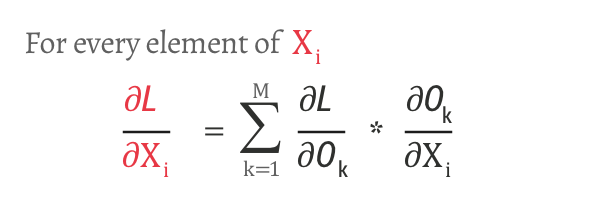
将其展开并代入方程 B,我们得到

好的。现在我们有了 ∂L/∂X 的值。不管你相信与否,这甚至可以表示为卷积运算。
∂L/∂X 可以表示为 180 度旋转滤波器 F 和损失梯度 ∂L/∂O 之间的“完全”卷积
首先,让我们将滤镜 F 旋转 180 度。这是通过先垂直翻转然后水平翻转来完成的。

现在,让我们在这个翻转的滤波器 F 和 ∂L/∂O 之间进行“完全”卷积,如下所示:(这就像将一个矩阵从右到左、从下到上滑动到另一个矩阵上)
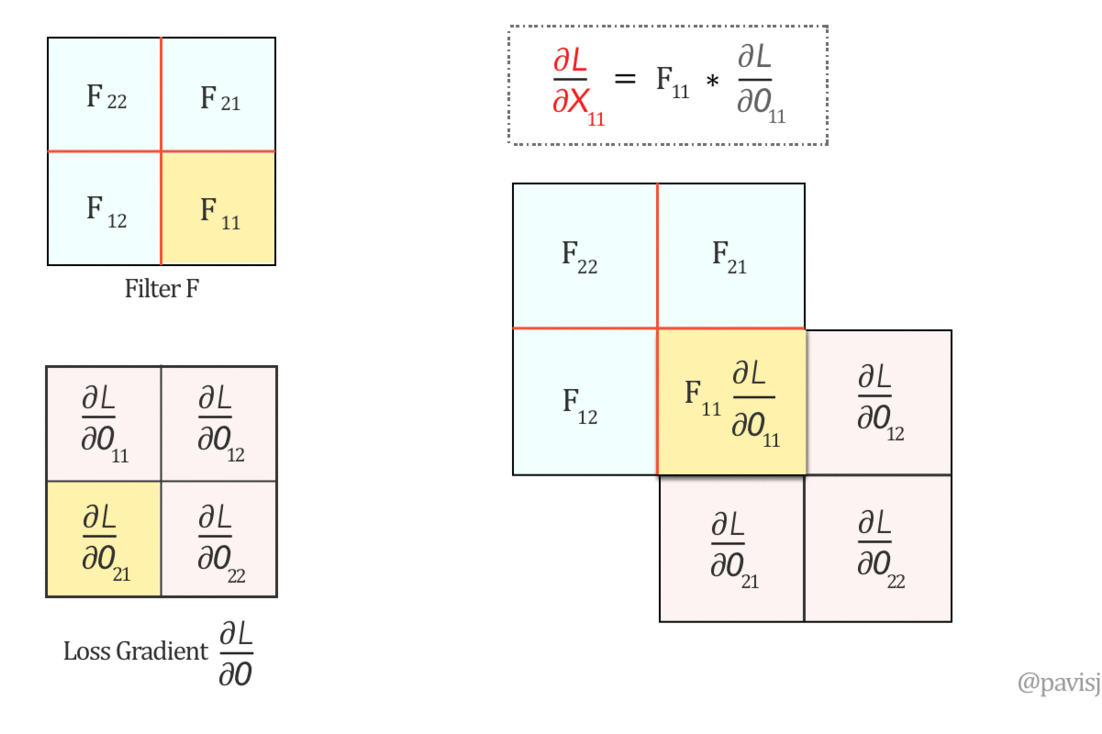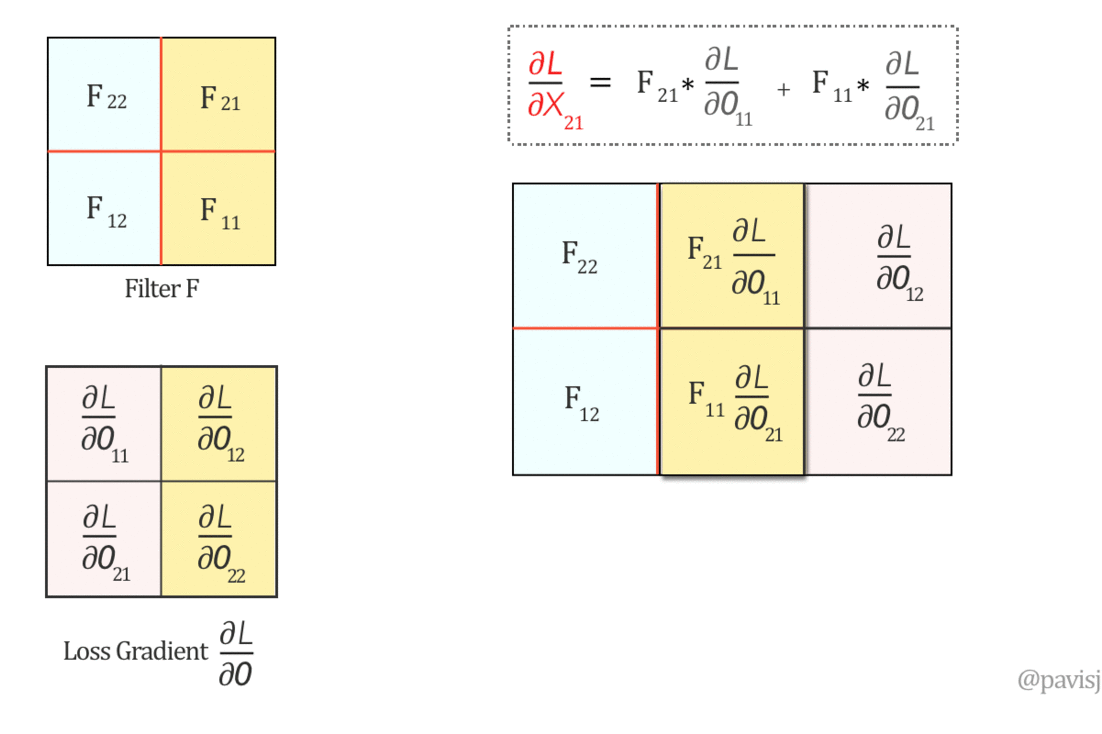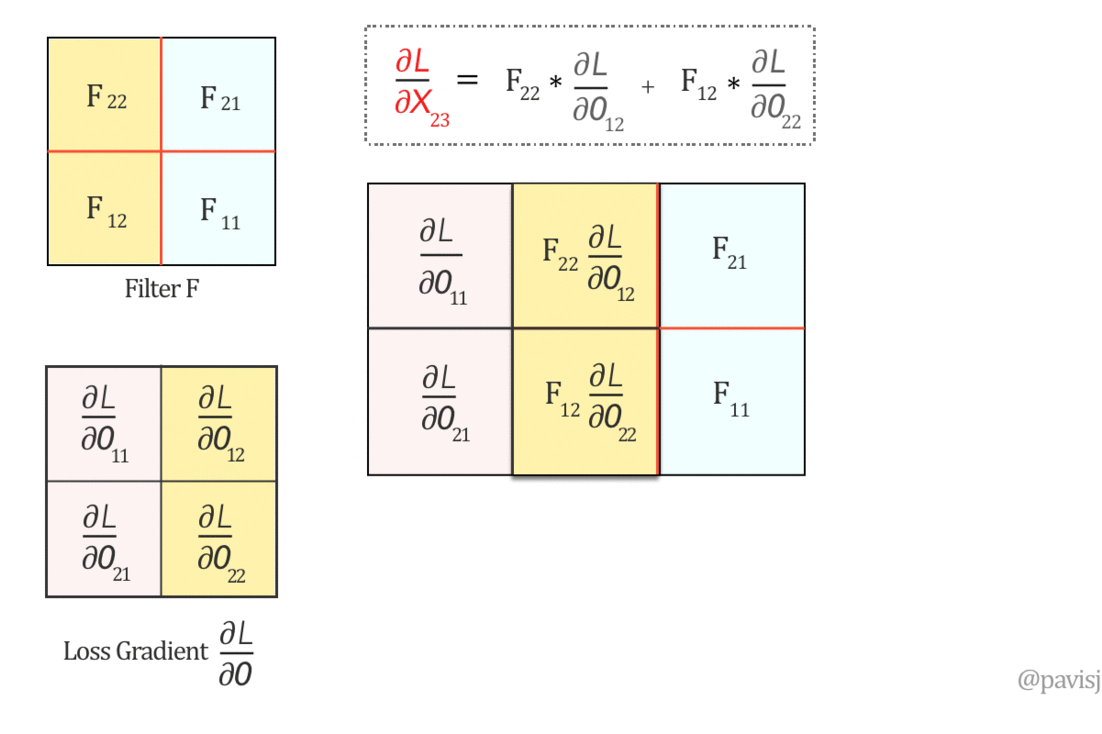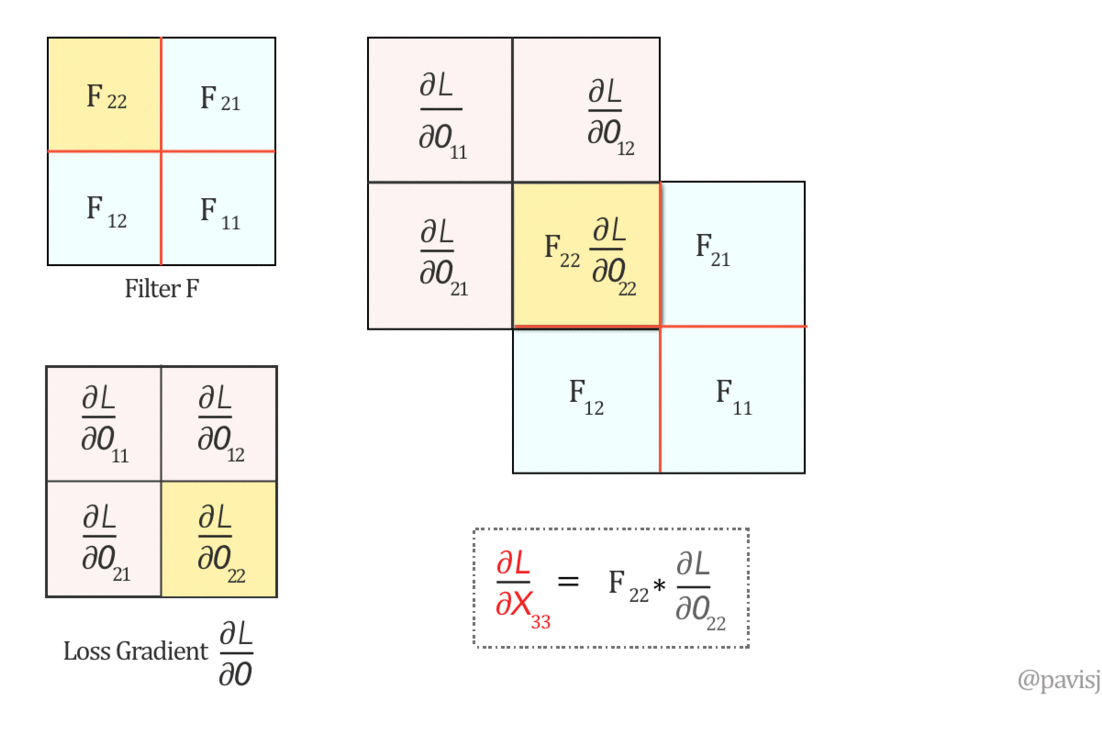
上面的全卷积生成 ∂L/∂X 的值,因此我们可以将 ∂L/∂X 表示为

好了,现在我们已经找到了∂L/∂X 和 ∂L/∂F,我们现在可以得出这个结论
卷积层的前向传播和反向传播都是卷积
总结一下:

五、结束语
希望这有助于解释反向传播在 CNN 卷积层中的工作原理。如果您想了解更多相关信息,请查看下面的链接。并通过为这篇文章鼓掌来表达一些爱。