一、轴角转换成旋转矩阵
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
double theta = M_PI/2;//90度
Eigen::Vector3d xyz(1, 0, 0);//x轴
Eigen::AngleAxisd rotation_vector(theta, xyz);
//Eigen::Matrix3d rotation_matrix = rotation_vector.matrix();
Eigen::Matrix3d rotation_matrix = rotation_vector.toRotationMatrix();
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(2); //使用定点计数法,显示小数点后面位数精度
cout << rotation_matrix << endl;
}结果:

二、旋转矩阵转换成轴角
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
Eigen::Matrix3d rotation_matrix;
rotation_matrix << 1, 0, 0, 0, 0, -1, 0, 1, 0;
/*Eigen::AngleAxisd v2;
v2.fromRotationMatrix(rotation_matrix);*/
/*Eigen::AngleAxisd v2;
v2 = rotation_matrix;*/
Eigen::AngleAxisd v2(rotation_matrix);
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(2); //使用定点计数法,显示小数点后面位数精度
cout << "轴角的角度:" << endl << (v2.angle() * 180 / M_PI) <<"度" << endl << "轴:" << endl << v2.axis() << endl;
}结果:

三、旋转矩阵转换成欧拉角
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
Eigen::Matrix3d rotation_matrix;
rotation_matrix << 1, 0, 0, 0, 0, -1, 0, 1, 0;//这是x旋转90度的旋转矩阵
Eigen::Vector3d eulerAngle = rotation_matrix.eulerAngles(2, 1, 0);//算出来的都是弧度制,指定顺序ZYX
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(2); //使用定点计数法,显示小数点后面位数精度
cout << eulerAngle*180/M_PI << endl;//转换成角度
}结果:

四、欧拉角转换成旋转矩阵
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
Eigen::Vector3d eulerAngle;
eulerAngle << 0, 0, 1.57;//90度的弧度值
Eigen::Matrix3d rotation_matrix;
rotation_matrix = Eigen::AngleAxisd(eulerAngle[0], Eigen::Vector3d::UnitZ()) * Eigen::AngleAxisd(eulerAngle[1], Eigen::Vector3d::UnitY()) * Eigen::AngleAxisd(eulerAngle[2], Eigen::Vector3d::UnitX());
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(2); //使用定点计数法,显示小数点后面位数精度
cout << rotation_matrix << endl;
}结果:
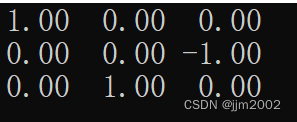
五、四元数转换成旋转矩阵
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
Eigen::Matrix3d rotation_matrix;
Eigen::Vector4d quat(0.707, 0.707, 0, 0);//x轴90度,输入时第一个为实部,输出时最后一个为实部
Eigen::Quaterniond quaternion(quat[0], quat[1], quat[2], quat[3]);
//rotation_matrix = quaternion.matrix()
rotation_matrix = quaternion.toRotationMatrix();
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(3); //使用定点计数法,显示小数点后面位数精度
cout << rotation_matrix << endl;
}
结果:

六、 旋转矩阵转换成四元数
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
Eigen::Matrix3d rotation_matrix;
rotation_matrix << 1, 0, 0, 0, 0, -1, 0, 1, 0;
Eigen::Quaterniond quaternion(rotation_matrix);
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(3); //使用定点计数法,显示小数点后面位数精度
cout << quaternion << endl;
}
结果:

七、轴角转换成四元数
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
double theta = M_PI/2;
Eigen::Vector3d xyz(1, 0, 0);
Eigen::AngleAxisd rotation_vector(theta, xyz);
Eigen::Quaterniond quaternion(rotation_vector);
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(3); //使用定点计数法,显示小数点后面位数精度
cout << quaternion << endl;
}
结果:

八、四元数转换成轴角
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
Eigen::Matrix3d rotation_matrix;
Eigen::Vector4d quat(0.707, 0.707, 0, 0);//x轴90度,输入时第一个为实部,输出时最后一个为实部
Eigen::Quaterniond quaternion(quat[0], quat[1], quat[2], quat[3]);
Eigen::AngleAxisd v2(quaternion);
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(3); //使用定点计数法,显示小数点后面位数精度
cout << "轴角的角度:" << endl << (v2.angle() * 180 / M_PI) <<"度" << endl << "轴:" << endl << v2.axis() << endl;
}
结果:

九、 轴角转换成欧拉角
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
double theta = M_PI/2;
Eigen::Vector3d xyz(1, 0, 0);
Eigen::AngleAxisd rotation_vector(theta, xyz);
Eigen::Vector3d eulerAngle = rotation_vector.matrix().eulerAngles(2, 1, 0);//zyx
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(3); //使用定点计数法,显示小数点后面位数精度
cout << eulerAngle << endl;
}
结果:
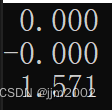
十、欧拉角转换成轴角
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
Eigen::Vector3d eulerAngle;
eulerAngle << 0, 0, 1.57;
Eigen::Matrix3d rotation_matrix;
Eigen::AngleAxisd rollAngle(Eigen::AngleAxisd(eulerAngle[2], Eigen::Vector3d::UnitX()));
Eigen::AngleAxisd pitchAngle(Eigen::AngleAxisd(eulerAngle[1], Eigen::Vector3d::UnitY()));
Eigen::AngleAxisd yawAngle(Eigen::AngleAxisd(eulerAngle[0], Eigen::Vector3d::UnitZ()));
Eigen::AngleAxisd v2;
v2 = yawAngle * pitchAngle * rollAngle;
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(0); //使用定点计数法,显示小数点后面位数精度
cout << "轴角的角度:" << endl << (v2.angle() * 180 / M_PI) <<"度" << endl << "轴:" << endl << v2.axis() << endl;
}
结果:

十一、 欧拉角转换成四元数
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
Eigen::Vector3d eulerAngle;
eulerAngle << 0, 0, 1.57;
Eigen::Quaterniond quaternion;
quaternion = Eigen::AngleAxisd(eulerAngle[0], Eigen::Vector3d::UnitZ()) * Eigen::AngleAxisd(eulerAngle[1], Eigen::Vector3d::UnitY()) * Eigen::AngleAxisd(eulerAngle[2], Eigen::Vector3d::UnitX());
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(3); //使用定点计数法,显示小数点后面位数精度
cout << quaternion << endl;
}
结果:
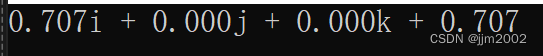
十二、 欧拉角转换成四元数
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
Eigen::Matrix3d rotation_matrix;
Eigen::Vector4d quat(0.707, 0.707, 0, 0);//x轴90度,输入时第一个为实部,输出时最后一个为实部
Eigen::Quaterniond quaternion(quat[0], quat[1], quat[2], quat[3]);
Eigen::Vector3d eulerAngle = quaternion.matrix().eulerAngles(2, 1, 0);
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(3); //使用定点计数法,显示小数点后面位数精度
cout << eulerAngle << endl;
}
结果:

十三、空间变换案例
C++实现
#include <iostream>
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <math.h>
using namespace std;
int main()
{
//将T初始化为单位阵,再做其他操作。
//虽然称为3D,实质上为4*4矩阵。
Eigen::Isometry3d T = Eigen::Isometry3d::Identity();
//设置旋转向量V
double theta = M_PI/2;
Eigen::Vector3d xyz(1, 0, 0);
Eigen::AngleAxisd V(theta, xyz);
//设置平移向量
Eigen::Vector3d translation(1, 3, 4);
T.rotate(V);
T.translate(translation);
//translate右乘,先旋转后平移
//结果为 1 0 0 1
// 0 1 0 3
// 0 0 1 4
// 0 0 0 1
//
//以及 1 0 0 0
// 0 0 -1 0
// 0 1 0 0
// 0 0 0 1
//第一个矩阵右乘第二个矩阵
//pretranslate左乘,先平移后旋转
/*T.rotate(V);
T.pretranslate(translation);*/
cout.setf(ios_base::fixed, ios_base::floatfield); //使用定点计数法,精度指的是小数点后面的位数,而不是总位数
cout.setf(ios_base::showpoint); //显示小数点后面的0
cout.precision(3); //使用定点计数法,显示小数点后面位数精度
cout << endl << T.matrix() << endl;
}
结果:
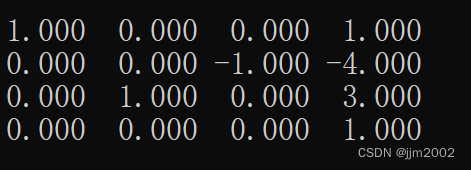


![[VulnHub靶机渗透] WestWild 1.1](https://img-blog.csdnimg.cn/direct/7a7bc257524d4cd6aa5a5aebbf23b393.png)