原题链接：https://www.acwing.com/problem/content/5472/

题目描述：

给定一个 n 个节点的无向树，节点编号 1∼n。

树上有两个不同的特殊点 x,y，对于树中的每一个点对 (u,v)(u≠v)，如果从 u 到 v 的最短路径需要经过点 x 和点 y（路径的两个端点也算经过），且相对顺序上先经过点 x，后经过点 y，那么就称 (u,v) 是一个无效点对，否则就称 (u,v) 是一个有效点对。

请你计算树中有效点对的数量。

注意：

1. (u,v) 和 (v,u) 是两个不同的点对。
2. 有效点对必须满足 u≠v。

输入输出描述：

输入格式

第一行包含三个整数 n,x,y。

接下来 n−1 行，每行包含两个整数 a,b，表示点 a 和点 b 之间存在一条无向边。

输出格式

一个整数，表示有效点对的数量。

数据范围

前 3 个测试点满足 1≤n≤10。
所有测试点满足 1≤n≤3×10^5，1≤x,y≤n，x≠y，1≤a,b≤n，a≠b。

输入样例1：

3 1 3
1 2
2 3

输出样例1：

5

输入样例2：

3 1 3
1 2
1 3

输出样例2：

4

解题思路：

这个题目的关键就在于巧妙选择根结点方便计算，还有一个非常常用的方法就是正难则反，如果直接计算有效点对，显然存在多种情况，直接计算比较困难，这个时候就应该想到正难则反了，无效点对指的是先经过x点，再经过y点的路径，这个比较好计算，总的点对数为n*(n-1)，只需要用总的点对数减去无效点对数就是有效点对数，下面画个图描述一下 ，如下图

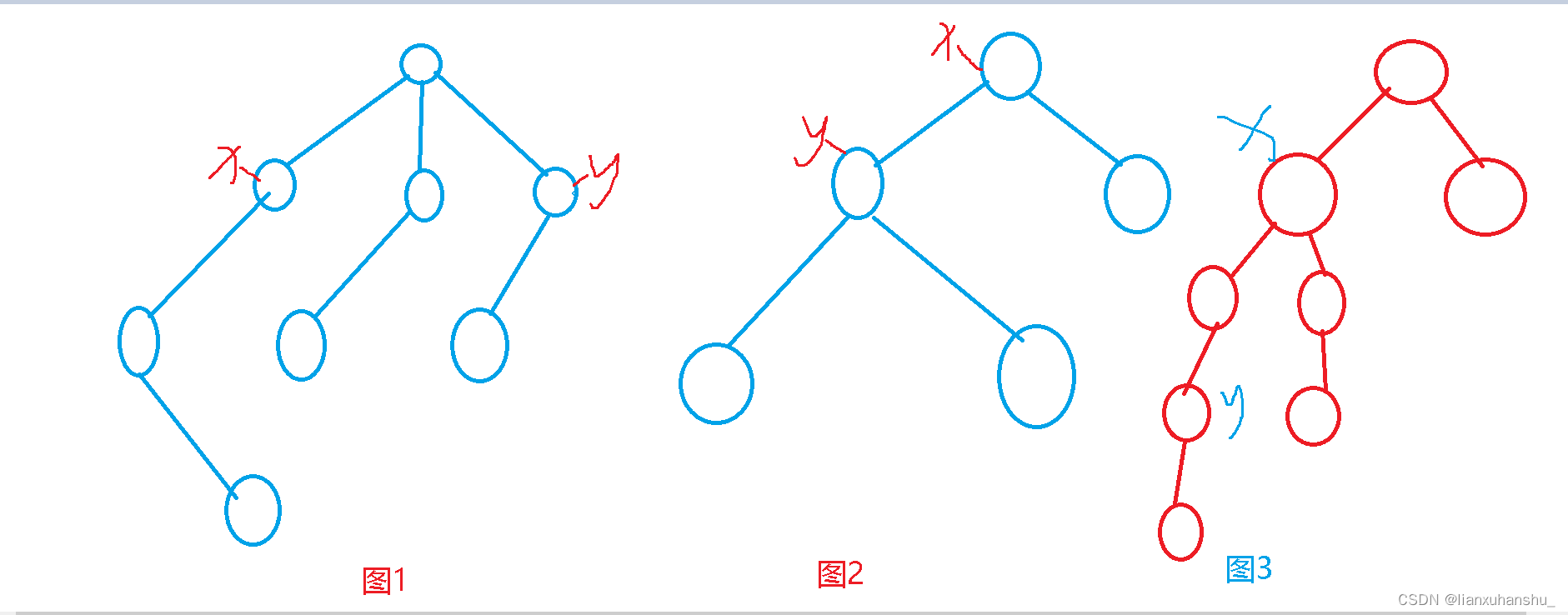
我们考虑以x，y路径之间的点为根节点，同时让x在上面，那么就只会出现图1和图2这种情况了，就方便计算了。

对于图1，假设以x为根节点的子树中结点的个数是sizex，以y为根结点的子树中结点个数为sizey，那么这种形式的树中无效点对个数为sizex*sizey，那么有效点对个数就是n*(n-1)-sizex*sizey。

对于图2，可以认为是图1的一种特殊情况，需要特判一下，假设以y为根节点的子树大小为sizey，那么无效点对的起点是y子树中的某个点，无效点对的终点是y子树之外的任意一个点，那么无效点对的数目就是sizey*(n-sizey)，那么有效点对的数目就是n*(n-1)-sizey*(n-sizey)。

对于图3，无效点对起点只能是y以及y以下的任意一个点，终点只能是x以及x以上的任意一个点，这个不是很好计算，我们可以以x，y路径上的某一个点为根节点，那么就可以避免图3这种情况，只需要考虑图1和图2这俩种情况即可，为了方便可以以y的父节点为根节点，那么就只需要考虑图1和图2这俩种情况了。

时间复杂度：O(n)，n表示点数，因为边数为n-1。

空间复杂度：O(n)。

cpp代码如下：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;
typedef long long LL;

const int N=3e5+10,M=N*2;

int n,x,y;
int h[N],e[M],ne[M],idx;
int fa[N];
int sizex,sizey;

void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void dfs1(int u,int father)
{
    fa[u]=father;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(j==father)continue;
        dfs1(j,u);
    }
}

int dfs2(int u,int father)
{
    int res=1;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(j==father)continue;
        int d=dfs2(j,u);
        res+=d;
        if(j==x)sizex=d;
        if(j==y)sizey=d;
    }
    return res;
}
int main()
{
    cin>>n>>x>>y;
    memset(h,-1,sizeof h);
    for(int i=0;i<n-1;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v),add(v,u);
    }
    
    dfs1(x,-1);  //第一个dfs是为了让x在上面,y在下面减少需要讨论的情况
    dfs2(fa[y],-1);  //第二个dfs以x,y路径上的某一个点为根节点方便计算,为了方便，不妨以y的父节点为根节点
    
    if(fa[y]==x){  //图2情况
        cout<<(LL)n*(n-1)-(LL)sizey*(n-sizey);
    }else {  //图1情况
        cout<<(LL)n*(n-1)-(LL)sizex*sizey;
    }
    return 0;
}