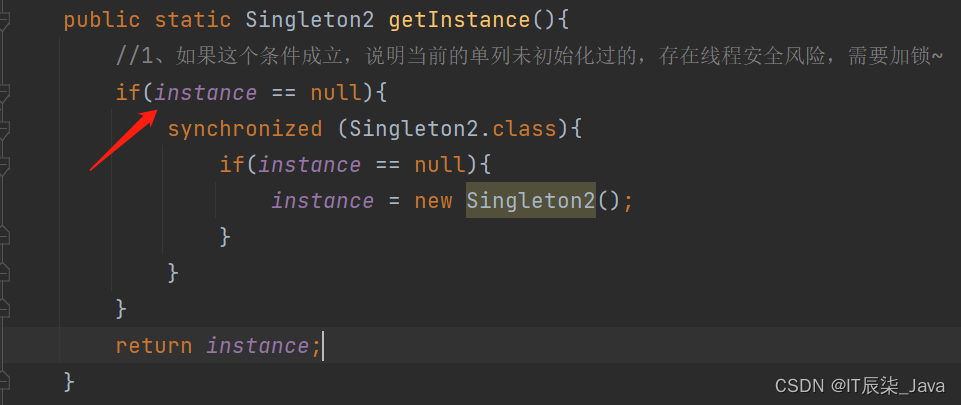
设平面有n个点的直角坐标是
,i = 1, 2, ...,n,求距离最近的2个点,距离计算:
首先这个问题是可以使用蛮力算法,一共n(n-1)/2个点对,每对点对计算需要常数的时间,蛮力算法需要的时间。
由于点对有二维的空间坐标,直觉上我们可以通过将平面进行划分,如图,用一条垂直线将集合P划分为和左右2部分,两部分点数近似相等,即
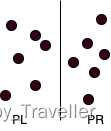
P中最临近点有3种情况:都在中,都在
中,或者一个点在
中,一个在
中。算法分别计算这3种情况。对于前两种情况,分别计算
中和
中的点对,这是2个n/2规模的子问题,对于第三种情况,需要找到由一个
和一个
中的点所构成的最邻近点对。假设
和
中的最邻近的点对的距离分别是
和
,令
,那么对于距离小于
的点对只可能出现在第3种情况,为了找到这样的点对,只需要寻找垂直线l两边距l不超过
的窄缝内的点即可。
MinDistance(P, X, Y)
input : n个点的集合P,X和Y分别给出P中点的橫、纵坐标
output : 最近的两个点及距离
1.如果P中点数小于等于3, 则直接计算其中的最小距离
2.排序X,Y
3.做垂直线l将P近似划分为大小相等的点集PL和PR,PL的点在l左边,PR的点在l的右边
4.MinDistance(PL, XL, YL); dL = PL中的最小距离
5.MinDistance(PR, XR, YR); dR = PR中的最小距离
6.d <- min(dL, dR)
7.对于在线l左边距离d范围内的每个点,检查l右边是否有点与它的距离小于d,如果存在则将d修改为新值行4和行5是递归调用,每个对应于n/2规模的子问题,行2的排序需要O(nlogn)时间,行3的划分基于行2的排序,不需要额外的计算。行6需要的时间是常数,所以只需要看行7的计算复杂度。如下图
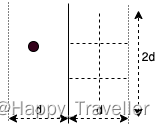
设左半部分的任意一点,在右边窄缝内距离该点小于d的点,其纵坐标一定在
和
之间,即右边窄缝里面的点一定位于右边长2d,宽d的框框里面,才有可能和
的距离小于d。将这个空间分成6份,每一个小矩形的对角线的长度是5d/6,说明在每一个小矩形内最多只能有1个点,因此,右边和
的距离小于d的点最多能有6个。对左边的每个点来说,检查另一边是否有点与它距离小于d,只需要检查常数个点。假设所有距线l不超过d的窄缝中的点构成集合S。只要S中点的纵坐标已经排好序(通过顺序扫描Y,检查每个点的橫坐标看它是否距l小于d。如果是,就把它放到S中。这需要额外O(n)时间,不超过行2的O(nlogn)排序时间),我们可以按照S中点的纵坐标顺序考察,比如说从具有最大纵坐标的点开始,顺序检查每个点。如果这个点的纵坐标是y,那么只需要检查那些纵坐标不小于y-d的点,看看其中是否存在分布在分布在另一侧,且与该点的距离小于d的点。上面已经证明在另一侧相关区域内的点不超过6个,而同侧区域的点也不会超过6个,因此这个检查之多需要考察12个纵坐标(如果高度是d,准确地说是不超过8个),这仅需要常数的时间。由于S的点数不超过n,因而对窄缝中所有点的检查需要O(n)时间。而这个时间也不超过行2的排序时间。于是,除了递归调用外,额外的工作时间是O(nlogn).
基于上面的分析,不难写出该算法时间复杂度的递推方程
根据主定理(Master Theorem)推导和理解(3)_Happy_Traveller的博客-CSDN博客
比起蛮力算法,已经有了明显的改进




![[VP]河南第十三届ICPC大学生程序竞赛 J.甜甜圈](https://img-blog.csdnimg.cn/2ecc13a54d97446da0de1f9cb138a341.png)