前言

传送门 : https://ac.nowcoder.com/acm/contest/17148/J

题意 :
给定两个甜甜圈堆 , 每次只能吃所有中最甜的那一个 , 否则的话就移动

询问最小的移动步骤

思路 :
很明确的一个目标 , 寻找当前最大值并且求出距离

那么我们考虑将两个甜甜圈堆进行合并 , 使得变成一个堆的操作

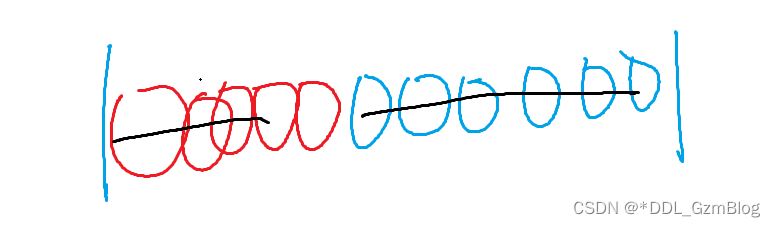
不难发现, 我们如果对甜度进行排序 ,那么最大值很容易就可以找到 , 而且对于距离的操作,我们只需要多记录一个下标即可 。 但是被吃掉的甜甜圈会消失 , 也就是我们计算完操作之后需要给他删除

所以我们就可以发现 , 如果我们利用树状数组前缀和的操作 , 那么两边的距离就是$getsum(i)-getsum(i-1)$

而对于每次的删除就是$updata(i,-1)$

code :

const int N = 2e5+10,INF = 0x3f3f3f3f;
const double eps = 1e-5;


struct node{
    int to,val;
};



ll c[N];
int n,m;
int lowbit(int x){return x&(-x);}

void updata(int i,int k)     
{
    while(i <= n + m) 
    {
        c[i] += k;
        i += lowbit(i); 
    }
}
ll getsum(int i){        
    ll res = 0;
    while(i > 0){
        res += c[i];
        i -= lowbit(i); 
    }
    return res;
}

pii a[N];
bool cmp(pii a,pii b){
	return a.x > b.x ;
}
void solve(){
	
	cin>>n>>m;
	
	
	for(int i = n ; i >= 1 ;i --  ){
		updata(i,1);
		cin>>a[i].x ;
		a[i].y = i ;
	}
	
	for(int i = n+1 ; i <= n + m ;i ++ ){
		updata(i,1);
		cin>>a[i].x;
		a[i].y = i ;
	}
	
	ll ans = 0 ;
	
	a[0].y = n;
	
	sort(a+1,a+1+n+m,cmp);
	
	for(int i = 1; i <= n  + m ;i ++ ){
		updata(a[i].y , -1);
		ans += abs(getsum(a[i].y) - getsum(a[i-1].y));
	}
	
	cout<<ans<<endl;
	
}