力扣刷题之旅：进阶篇（四）—

力扣刷题之旅：进阶篇（四）—— 滑动窗口问题

news2024/11/17 20:25:09

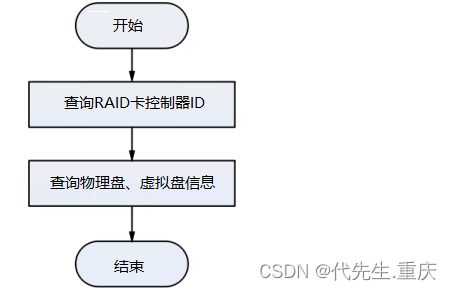
力扣（LeetCode）是一个在线编程平台，主要用于帮助程序员提升算法和数据结构方面的能力。以下是一些力扣上的入门题目，以及它们的解题代码。

--点击进入刷题地址

引言：

在编程的世界里，滑动窗口问题是一种常见且具有挑战性的问题类型。在力扣（LeetCode）上，这类问题往往以其独特的思维方式和高难度的解法吸引着众多算法爱好者。今天，我们就来一起探讨一道滑动窗口的经典题目：“最小覆盖子串”。

题目描述：

-- 给定一个字符串 S 和一个字符串 T，找出 S 中最短的子串，使得 T 是 S 的子序列。如果 S 中不存在这样的子串，就返回一个空字符串。

示例：

输入:

S = "ADOBECODEBANC"
T = "ABC"

输出:

"BANC"

解题思路：

        这道题目的关键在于理解子序列和子串的区别。子序列是指从原序列中删除一些元素（也可以不删除）后得到的序列，而子串则是指原序列中连续的一段。因此，我们需要找到一个尽可能短的子串，使得这个子串包含了 T 中的所有字符。
        为了解决这个问题，我们可以使用滑动窗口的思想。首先，我们使用双指针来定义一个窗口，这个窗口包含了 T 中的所有字符。然后，我们尝试缩小这个窗口的大小，直到无法再缩小为止。最后，我们就得到了一个包含 T 的最短子串。
        具体实现时，我们可以使用哈希表来记录 T 中每个字符的出现次数。然后，我们遍历 S，用一个变量来记录当前窗口中已经包含了 T 中的多少个字符。当这个变量等于 T 的长度时，说明我们已经找到了一个包含 T 的子串。此时，我们可以尝试缩小窗口的大小，直到无法再缩小为止。

代码实现：

def minWindow(s: str, t: str) -> str:  
    if not s or not t or len(s) < len(t):  
        return ""  
      
    # 记录 t 中每个字符的出现次数  
    target_count = {}  
    for char in t:  
        target_count[char] = target_count.get(char, 0) + 1  
      
    # 使用滑动窗口来查找最短子串  
    left, right = 0, 0  # 窗口的左右指针  
    formed = 0  # 记录当前窗口中已经包含了 t 中的多少个字符  
    min_len = float('inf')  # 最小子串的长度  
    min_left = min_right = 0  # 最小子串的左右指针  
      
    while right < len(s):  
        char = s[right]  
        right += 1  
          
        # 如果当前字符在 t 中出现过，则增加 formed 的计数  
        if char in target_count:  
            formed += 1  
              
        # 当 formed 的计数等于 t 的长度时，说明已经找到了一个包含 t 的子串  
        while formed == len(t):  
            # 更新最小子串的长度和左右指针  
            if right - left < min_len:  
                min_len = right - left  
                min_left = left  
                min_right = right  
              
            char = s[left]  
            left += 1  
              
            # 如果当前字符在 t 中出现过，则减少 formed 的计数  
            if char in target_count:  
                formed -= 1  
      
    return s[min_left:min_right] if min_len != float('inf') else ""